Zero-Shot Learning of Causal Models
Paper and Code
Oct 08, 2024


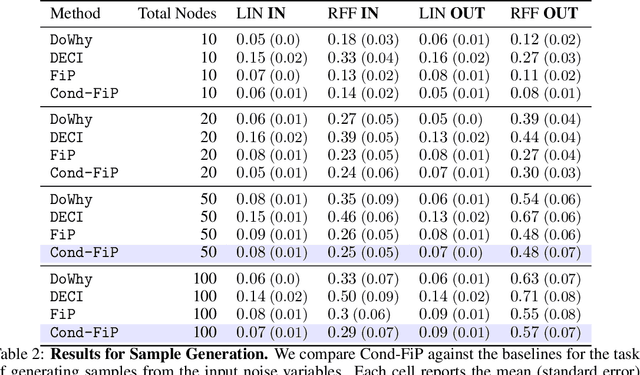
With the increasing acquisition of datasets over time, we now have access to precise and varied descriptions of the world, capturing all sorts of phenomena. These datasets can be seen as empirical observations of unknown causal generative processes, which can commonly be described by Structural Causal Models (SCMs). Recovering these causal generative processes from observations poses formidable challenges, and often require to learn a specific generative model for each dataset. In this work, we propose to learn a \emph{single} model capable of inferring in a zero-shot manner the causal generative processes of datasets. Rather than learning a specific SCM for each dataset, we enable the Fixed-Point Approach (FiP) proposed in~\cite{scetbon2024fip}, to infer the generative SCMs conditionally on their empirical representations. More specifically, we propose to amortize the learning of a conditional version of FiP to infer generative SCMs from observations and causal structures on synthetically generated datasets. We show that our model is capable of predicting in zero-shot the true generative SCMs, and as a by-product, of (i) generating new dataset samples, and (ii) inferring intervened ones. Our experiments demonstrate that our amortized procedure achieves performances on par with SoTA methods trained specifically for each dataset on both in and out-of-distribution problems. To the best of our knowledge, this is the first time that SCMs are inferred in a zero-shot manner from observations, paving the way for a paradigmatic shift towards the assimilation of causal knowledge across datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge