Amortizing Maximum Inner Product Search with Learned Support Functions

Maximum inner product search (MIPS) is a crucial subroutine in machine learning, requiring the identification of key vectors that align best with a given query. We propose amortized MIPS: a learning-based approach that trains neural networks to directly predict MIPS solutions, amortizing the computational cost of matching queries (drawn from a fixed distribution) to a fixed set of keys. Our key insight is that the MIPS value function, the maximal inner product between a query and keys, is also known as the support function of the set of keys. Support functions are convex, 1-homogeneous and their gradient w.r.t. the query is exactly the optimal key in the database. We approximate the support function using two complementary approaches: (1) we train an input-convex neural network (SupportNet) to model the support function directly; the optimal key can be recovered via (autodiff) gradient computation, and (2) we regress directly the optimal key from the query using a vector valued network (KeyNet), bypassing gradient computation entirely at inference time. To learn a SupportNet, we combine score regression with gradient matching losses, and propose homogenization wrappers that enforce the positive 1-homogeneity of a neural network, theoretically linking function values to gradients. To train a KeyNet, we introduce a score consistency loss derived from the Euler theorem for homogeneous functions. Our experiments show that learned SupportNet or KeyNet achieve high match rates and open up new directions to compress databases with a specific query distribution in mind.

The Coupling Within: Flow Matching via Distilled Normalizing Flows

Flow models have rapidly become the go-to method for training and deploying large-scale generators, owing their success to inference-time flexibility via adjustable integration steps. A crucial ingredient in flow training is the choice of coupling measure for sampling noise/data pairs that define the flow matching (FM) regression loss. While FM training defaults usually to independent coupling, recent works show that adaptive couplings informed by noise/data distributions (e.g., via optimal transport, OT) improve both model training and inference. We radicalize this insight by shifting the paradigm: rather than computing adaptive couplings directly, we use distilled couplings from a different, pretrained model capable of placing noise and data spaces in bijection -- a property intrinsic to normalizing flows (NF) through their maximum likelihood and invertibility requirements. Leveraging recent advances in NF image generation via auto-regressive (AR) blocks, we propose Normalized Flow Matching (NFM), a new method that distills the quasi-deterministic coupling of pretrained NF models to train student flow models. These students achieve the best of both worlds: significantly outperforming flow models trained with independent or even OT couplings, while also improving on the teacher AR-NF model.

Completed Hyperparameter Transfer across Modules, Width, Depth, Batch and Duration

Hyperparameter tuning can dramatically impact training stability and final performance of large-scale models. Recent works on neural network parameterisations, such as $μ$P, have enabled transfer of optimal global hyperparameters across model sizes. These works propose an empirical practice of search for optimal global base hyperparameters at a small model size, and transfer to a large size. We extend these works in two key ways. To handle scaling along most important scaling axes, we propose the Complete$^{(d)}$ Parameterisation that unifies scaling in width and depth -- using an adaptation of CompleteP -- as well as in batch-size and training duration. Secondly, with our parameterisation, we investigate per-module hyperparameter optimisation and transfer. We characterise the empirical challenges of navigating the high-dimensional hyperparameter landscape, and propose practical guidelines for tackling this optimisation problem. We demonstrate that, with the right parameterisation, hyperparameter transfer holds even in the per-module hyperparameter regime. Our study covers an extensive range of optimisation hyperparameters of modern models: learning rates, AdamW parameters, weight decay, initialisation scales, and residual block multipliers. Our experiments demonstrate significant training speed improvements in Large Language Models with the transferred per-module hyperparameters.

The Data-Quality Illusion: Rethinking Classifier-Based Quality Filtering for LLM Pretraining

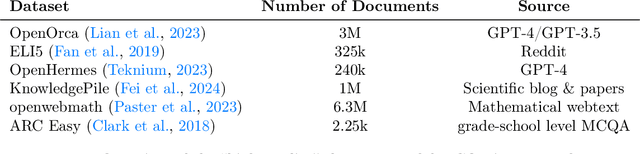
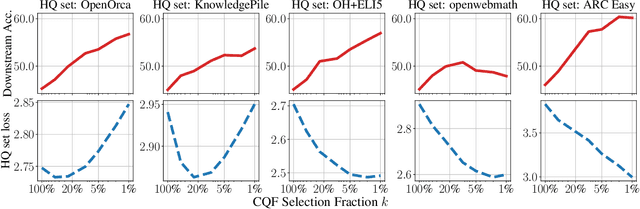
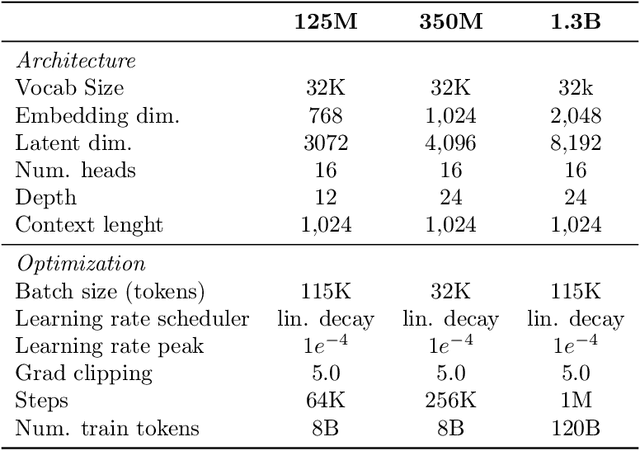
Large-scale models are pretrained on massive web-crawled datasets containing documents of mixed quality, making data filtering essential. A popular method is Classifier-based Quality Filtering (CQF), which trains a binary classifier to distinguish between pretraining data and a small, high-quality set. It assigns each pretraining document a quality score defined as the classifier's score and retains only the top-scoring ones. We provide an in-depth analysis of CQF. We show that while CQF improves downstream task performance, it does not necessarily enhance language modeling on the high-quality dataset. We explain this paradox by the fact that CQF implicitly filters the high-quality dataset as well. We further compare the behavior of models trained with CQF to those trained on synthetic data of increasing quality, obtained via random token permutations, and find starkly different trends. Our results challenge the view that CQF captures a meaningful notion of data quality.

The Geometries of Truth Are Orthogonal Across Tasks

Large Language Models (LLMs) have demonstrated impressive generalization capabilities across various tasks, but their claim to practical relevance is still mired by concerns on their reliability. Recent works have proposed examining the activations produced by an LLM at inference time to assess whether its answer to a question is correct. Some works claim that a "geometry of truth" can be learned from examples, in the sense that the activations that generate correct answers can be distinguished from those leading to mistakes with a linear classifier. In this work, we underline a limitation of these approaches: we observe that these "geometries of truth" are intrinsically task-dependent and fail to transfer across tasks. More precisely, we show that linear classifiers trained across distinct tasks share little similarity and, when trained with sparsity-enforcing regularizers, have almost disjoint supports. We show that more sophisticated approaches (e.g., using mixtures of probes and tasks) fail to overcome this limitation, likely because activation vectors commonly used to classify answers form clearly separated clusters when examined across tasks.

On Fitting Flow Models with Large Sinkhorn Couplings

Flow models transform data gradually from one modality (e.g. noise) onto another (e.g. images). Such models are parameterized by a time-dependent velocity field, trained to fit segments connecting pairs of source and target points. When the pairing between source and target points is given, training flow models boils down to a supervised regression problem. When no such pairing exists, as is the case when generating data from noise, training flows is much harder. A popular approach lies in picking source and target points independently. This can, however, lead to velocity fields that are slow to train, but also costly to integrate at inference time. In theory, one would greatly benefit from training flow models by sampling pairs from an optimal transport (OT) measure coupling source and target, since this would lead to a highly efficient flow solving the Benamou and Brenier dynamical OT problem. In practice, recent works have proposed to sample mini-batches of $n$ source and $n$ target points and reorder them using an OT solver to form better pairs. These works have advocated using batches of size $n\approx 256$, and considered OT solvers that return couplings that are either sharp (using e.g. the Hungarian algorithm) or blurred (using e.g. entropic regularization, a.k.a. Sinkhorn). We follow in the footsteps of these works by exploring the benefits of increasing $n$ by three to four orders of magnitude, and look more carefully on the effect of the entropic regularization $\varepsilon$ used in the Sinkhorn algorithm. Our analysis is facilitated by new scale invariant quantities to report the sharpness of a coupling, while our sharded computations across multiple GPU or GPU nodes allow scaling up $n$. We show that in both synthetic and image generation tasks, flow models greatly benefit when fitted with large Sinkhorn couplings, with a low entropic regularization $\varepsilon$.

Multivariate Conformal Prediction using Optimal Transport

Conformal prediction (CP) quantifies the uncertainty of machine learning models by constructing sets of plausible outputs. These sets are constructed by leveraging a so-called conformity score, a quantity computed using the input point of interest, a prediction model, and past observations. CP sets are then obtained by evaluating the conformity score of all possible outputs, and selecting them according to the rank of their scores. Due to this ranking step, most CP approaches rely on a score functions that are univariate. The challenge in extending these scores to multivariate spaces lies in the fact that no canonical order for vectors exists. To address this, we leverage a natural extension of multivariate score ranking based on optimal transport (OT). Our method, OTCP, offers a principled framework for constructing conformal prediction sets in multidimensional settings, preserving distribution-free coverage guarantees with finite data samples. We demonstrate tangible gains in a benchmark dataset of multivariate regression problems and address computational \& statistical trade-offs that arise when estimating conformity scores through OT maps.

Multimodal Autoregressive Pre-training of Large Vision Encoders

We introduce a novel method for pre-training of large-scale vision encoders. Building on recent advancements in autoregressive pre-training of vision models, we extend this framework to a multimodal setting, i.e., images and text. In this paper, we present AIMV2, a family of generalist vision encoders characterized by a straightforward pre-training process, scalability, and remarkable performance across a range of downstream tasks. This is achieved by pairing the vision encoder with a multimodal decoder that autoregressively generates raw image patches and text tokens. Our encoders excel not only in multimodal evaluations but also in vision benchmarks such as localization, grounding, and classification. Notably, our AIMV2-3B encoder achieves 89.5% accuracy on ImageNet-1k with a frozen trunk. Furthermore, AIMV2 consistently outperforms state-of-the-art contrastive models (e.g., CLIP, SigLIP) in multimodal image understanding across diverse settings.

Controlling Language and Diffusion Models by Transporting Activations

The increasing capabilities of large generative models and their ever more widespread deployment have raised concerns about their reliability, safety, and potential misuse. To address these issues, recent works have proposed to control model generation by steering model activations in order to effectively induce or prevent the emergence of concepts or behaviors in the generated output. In this paper we introduce Activation Transport (AcT), a general framework to steer activations guided by optimal transport theory that generalizes many previous activation-steering works. AcT is modality-agnostic and provides fine-grained control over the model behavior with negligible computational overhead, while minimally impacting model abilities. We experimentally show the effectiveness and versatility of our approach by addressing key challenges in large language models (LLMs) and text-to-image diffusion models (T2Is). For LLMs, we show that AcT can effectively mitigate toxicity, induce arbitrary concepts, and increase their truthfulness. In T2Is, we show how AcT enables fine-grained style control and concept negation.

Simple ReFlow: Improved Techniques for Fast Flow Models

Diffusion and flow-matching models achieve remarkable generative performance but at the cost of many sampling steps, this slows inference and limits applicability to time-critical tasks. The ReFlow procedure can accelerate sampling by straightening generation trajectories. However, ReFlow is an iterative procedure, typically requiring training on simulated data, and results in reduced sample quality. To mitigate sample deterioration, we examine the design space of ReFlow and highlight potential pitfalls in prior heuristic practices. We then propose seven improvements for training dynamics, learning and inference, which are verified with thorough ablation studies on CIFAR10 $32 \times 32$, AFHQv2 $64 \times 64$, and FFHQ $64 \times 64$. Combining all our techniques, we achieve state-of-the-art FID scores (without / with guidance, resp.) for fast generation via neural ODEs: $2.23$ / $1.98$ on CIFAR10, $2.30$ / $1.91$ on AFHQv2, $2.84$ / $2.67$ on FFHQ, and $3.49$ / $1.74$ on ImageNet-64, all with merely $9$ neural function evaluations.