Composition and Control with Distilled Energy Diffusion Models and Sequential Monte Carlo

Diffusion models may be formulated as a time-indexed sequence of energy-based models, where the score corresponds to the negative gradient of an energy function. As opposed to learning the score directly, an energy parameterization is attractive as the energy itself can be used to control generation via Monte Carlo samplers. Architectural constraints and training instability in energy parameterized models have so far yielded inferior performance compared to directly approximating the score or denoiser. We address these deficiencies by introducing a novel training regime for the energy function through distillation of pre-trained diffusion models, resembling a Helmholtz decomposition of the score vector field. We further showcase the synergies between energy and score by casting the diffusion sampling procedure as a Feynman Kac model where sampling is controlled using potentials from the learnt energy functions. The Feynman Kac model formalism enables composition and low temperature sampling through sequential Monte Carlo.

Mechanisms of Projective Composition of Diffusion Models

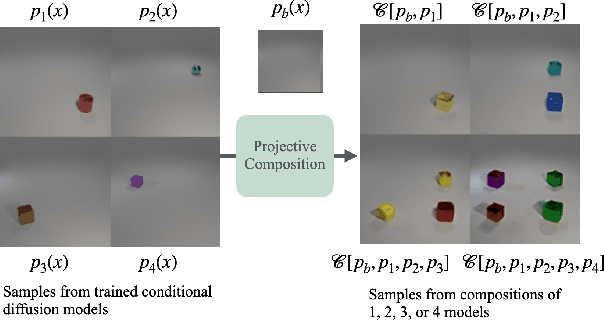
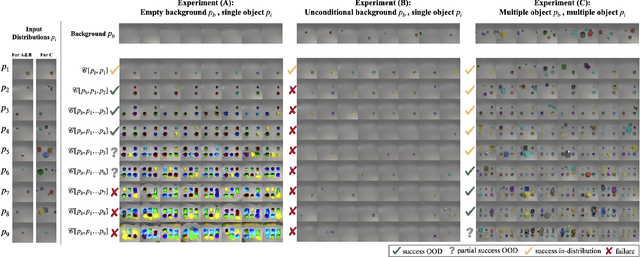
We study the theoretical foundations of composition in diffusion models, with a particular focus on out-of-distribution extrapolation and length-generalization. Prior work has shown that composing distributions via linear score combination can achieve promising results, including length-generalization in some cases (Du et al., 2023; Liu et al., 2022). However, our theoretical understanding of how and why such compositions work remains incomplete. In fact, it is not even entirely clear what it means for composition to "work". This paper starts to address these fundamental gaps. We begin by precisely defining one possible desired result of composition, which we call projective composition. Then, we investigate: (1) when linear score combinations provably achieve projective composition, (2) whether reverse-diffusion sampling can generate the desired composition, and (3) the conditions under which composition fails. Finally, we connect our theoretical analysis to prior empirical observations where composition has either worked or failed, for reasons that were unclear at the time.

Simple ReFlow: Improved Techniques for Fast Flow Models

Diffusion and flow-matching models achieve remarkable generative performance but at the cost of many sampling steps, this slows inference and limits applicability to time-critical tasks. The ReFlow procedure can accelerate sampling by straightening generation trajectories. However, ReFlow is an iterative procedure, typically requiring training on simulated data, and results in reduced sample quality. To mitigate sample deterioration, we examine the design space of ReFlow and highlight potential pitfalls in prior heuristic practices. We then propose seven improvements for training dynamics, learning and inference, which are verified with thorough ablation studies on CIFAR10 $32 \times 32$, AFHQv2 $64 \times 64$, and FFHQ $64 \times 64$. Combining all our techniques, we achieve state-of-the-art FID scores (without / with guidance, resp.) for fast generation via neural ODEs: $2.23$ / $1.98$ on CIFAR10, $2.30$ / $1.91$ on AFHQv2, $2.84$ / $2.67$ on FFHQ, and $3.49$ / $1.74$ on ImageNet-64, all with merely $9$ neural function evaluations.

Sparse Repellency for Shielded Generation in Text-to-image Diffusion Models

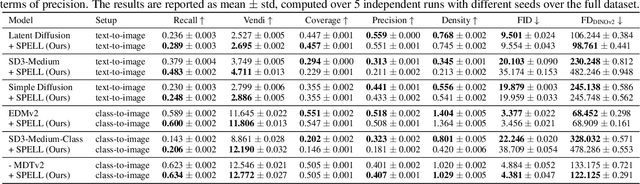
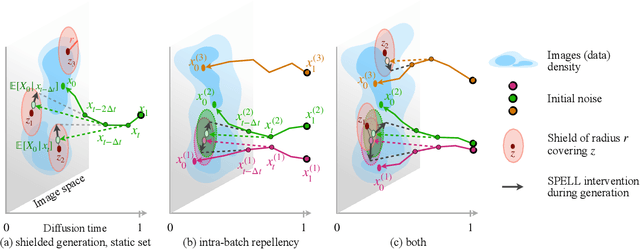
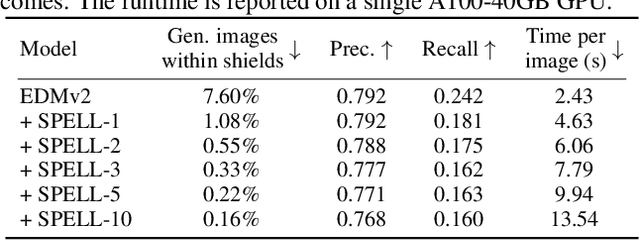
The increased adoption of diffusion models in text-to-image generation has triggered concerns on their reliability. Such models are now closely scrutinized under the lens of various metrics, notably calibration, fairness, or compute efficiency. We focus in this work on two issues that arise when deploying these models: a lack of diversity when prompting images, and a tendency to recreate images from the training set. To solve both problems, we propose a method that coaxes the sampled trajectories of pretrained diffusion models to land on images that fall outside of a reference set. We achieve this by adding repellency terms to the diffusion SDE throughout the generation trajectory, which are triggered whenever the path is expected to land too closely to an image in the shielded reference set. Our method is sparse in the sense that these repellency terms are zero and inactive most of the time, and even more so towards the end of the generation trajectory. Our method, named SPELL for sparse repellency, can be used either with a static reference set that contains protected images, or dynamically, by updating the set at each timestep with the expected images concurrently generated within a batch. We show that adding SPELL to popular diffusion models improves their diversity while impacting their FID only marginally, and performs comparatively better than other recent training-free diversity methods. We also demonstrate how SPELL can ensure a shielded generation away from a very large set of protected images by considering all 1.2M images from ImageNet as the protected set.

Differentiable Cost-Parameterized Monge Map Estimators

Within the field of optimal transport (OT), the choice of ground cost is crucial to ensuring that the optimality of a transport map corresponds to usefulness in real-world applications. It is therefore desirable to use known information to tailor cost functions and hence learn OT maps which are adapted to the problem at hand. By considering a class of neural ground costs whose Monge maps have a known form, we construct a differentiable Monge map estimator which can be optimized to be consistent with known information about an OT map. In doing so, we simultaneously learn both an OT map estimator and a corresponding adapted cost function. Through suitable choices of loss function, our method provides a general approach for incorporating prior information about the Monge map itself when learning adapted OT maps and cost functions.

Progressive Entropic Optimal Transport Solvers

Optimal transport (OT) has profoundly impacted machine learning by providing theoretical and computational tools to realign datasets. In this context, given two large point clouds of sizes $n$ and $m$ in $\mathbb{R}^d$, entropic OT (EOT) solvers have emerged as the most reliable tool to either solve the Kantorovich problem and output a $n\times m$ coupling matrix, or to solve the Monge problem and learn a vector-valued push-forward map. While the robustness of EOT couplings/maps makes them a go-to choice in practical applications, EOT solvers remain difficult to tune because of a small but influential set of hyperparameters, notably the omnipresent entropic regularization strength $\varepsilon$. Setting $\varepsilon$ can be difficult, as it simultaneously impacts various performance metrics, such as compute speed, statistical performance, generalization, and bias. In this work, we propose a new class of EOT solvers (ProgOT), that can estimate both plans and transport maps. We take advantage of several opportunities to optimize the computation of EOT solutions by dividing mass displacement using a time discretization, borrowing inspiration from dynamic OT formulations, and conquering each of these steps using EOT with properly scheduled parameters. We provide experimental evidence demonstrating that ProgOT is a faster and more robust alternative to standard solvers when computing couplings at large scales, even outperforming neural network-based approaches. We also prove statistical consistency of our approach for estimating optimal transport maps.

Contrasting Multiple Representations with the Multi-Marginal Matching Gap

Learning meaningful representations of complex objects that can be seen through multiple ($k\geq 3$) views or modalities is a core task in machine learning. Existing methods use losses originally intended for paired views, and extend them to $k$ views, either by instantiating $\tfrac12k(k-1)$ loss-pairs, or by using reduced embeddings, following a \textit{one vs. average-of-rest} strategy. We propose the multi-marginal matching gap (M3G), a loss that borrows tools from multi-marginal optimal transport (MM-OT) theory to simultaneously incorporate all $k$ views. Given a batch of $n$ points, each seen as a $k$-tuple of views subsequently transformed into $k$ embeddings, our loss contrasts the cost of matching these $n$ ground-truth $k$-tuples with the MM-OT polymatching cost, which seeks $n$ optimally arranged $k$-tuples chosen within these $n\times k$ vectors. While the exponential complexity $O(n^k$) of the MM-OT problem may seem daunting, we show in experiments that a suitable generalization of the Sinkhorn algorithm for that problem can scale to, e.g., $k=3\sim 6$ views using mini-batches of size $64~\sim128$. Our experiments demonstrate improved performance over multiview extensions of pairwise losses, for both self-supervised and multimodal tasks.

Careful with that Scalpel: Improving Gradient Surgery with an EMA

Beyond minimizing a single training loss, many deep learning estimation pipelines rely on an auxiliary objective to quantify and encourage desirable properties of the model (e.g. performance on another dataset, robustness, agreement with a prior). Although the simplest approach to incorporating an auxiliary loss is to sum it with the training loss as a regularizer, recent works have shown that one can improve performance by blending the gradients beyond a simple sum; this is known as gradient surgery. We cast the problem as a constrained minimization problem where the auxiliary objective is minimized among the set of minimizers of the training loss. To solve this bilevel problem, we follow a parameter update direction that combines the training loss gradient and the orthogonal projection of the auxiliary gradient to the training gradient. In a setting where gradients come from mini-batches, we explain how, using a moving average of the training loss gradients, we can carefully maintain this critical orthogonality property. We demonstrate that our method, Bloop, can lead to much better performances on NLP and vision experiments than other gradient surgery methods without EMA.

Riemannian Diffusion Schrödinger Bridge

Score-based generative models exhibit state of the art performance on density estimation and generative modeling tasks. These models typically assume that the data geometry is flat, yet recent extensions have been developed to synthesize data living on Riemannian manifolds. Existing methods to accelerate sampling of diffusion models are typically not applicable in the Riemannian setting and Riemannian score-based methods have not yet been adapted to the important task of interpolation of datasets. To overcome these issues, we introduce \emph{Riemannian Diffusion Schr\"odinger Bridge}. Our proposed method generalizes Diffusion Schr\"odinger Bridge introduced in \cite{debortoli2021neurips} to the non-Euclidean setting and extends Riemannian score-based models beyond the first time reversal. We validate our proposed method on synthetic data and real Earth and climate data.

Rethinking Initialization of the Sinkhorn Algorithm

Computing an optimal transport (OT) coupling between distributions plays an increasingly important role in machine learning. While OT problems can be solved as linear programs, adding an entropic smoothing term is known to result in solvers that are faster and more robust to outliers, differentiable and easier to parallelize. The Sinkhorn fixed point algorithm is the cornerstone of these approaches, and, as a result, multiple attempts have been made to shorten its runtime using, for instance, annealing, momentum or acceleration. The premise of this paper is that \textit{initialization} of the Sinkhorn algorithm has received comparatively little attention, possibly due to two preconceptions: as the regularized OT problem is convex, it may not be worth crafting a tailored initialization as \textit{any} is guaranteed to work; secondly, because the Sinkhorn algorithm is often differentiated in end-to-end pipelines, data-dependent initializations could potentially bias gradient estimates obtained by unrolling iterations. We challenge this conventional wisdom and show that carefully chosen initializations can result in dramatic speed-ups, and will not bias gradients which are computed with implicit differentiation. We detail how initializations can be recovered from closed-form or approximate OT solutions, using known results in the 1D or Gaussian settings. We show empirically that these initializations can be used off-the-shelf, with little to no tuning, and result in consistent speed-ups for a variety of OT problems.