Target Score Matching

Denoising Score Matching estimates the score of a noised version of a target distribution by minimizing a regression loss and is widely used to train the popular class of Denoising Diffusion Models. A well known limitation of Denoising Score Matching, however, is that it yields poor estimates of the score at low noise levels. This issue is particularly unfavourable for problems in the physical sciences and for Monte Carlo sampling tasks for which the score of the clean original target is known. Intuitively, estimating the score of a slightly noised version of the target should be a simple task in such cases. In this paper, we address this shortcoming and show that it is indeed possible to leverage knowledge of the target score. We present a Target Score Identity and corresponding Target Score Matching regression loss which allows us to obtain score estimates admitting favourable properties at low noise levels.

Metropolis Sampling for Constrained Diffusion Models

Denoising diffusion models have recently emerged as the predominant paradigm for generative modelling. Their extension to Riemannian manifolds has facilitated their application to an array of problems in the natural sciences. Yet, in many practical settings, such manifolds are defined by a set of constraints and are not covered by the existing (Riemannian) diffusion model methodology. Recent work has attempted to address this issue by employing novel noising processes based on logarithmic barrier methods or reflected Brownian motions. However, the associated samplers are computationally burdensome as the complexity of the constraints increases. In this paper, we introduce an alternative simple noising scheme based on Metropolis sampling that affords substantial gains in computational efficiency and empirical performance compared to the earlier samplers. Of independent interest, we prove that this new process corresponds to a valid discretisation of the reflected Brownian motion. We demonstrate the scalability and flexibility of our approach on a range of problem settings with convex and non-convex constraints, including applications from geospatial modelling, robotics and protein design.

Diffusion Models for Constrained Domains

Denoising diffusion models are a recent class of generative models which achieve state-of-the-art results in many domains such as unconditional image generation and text-to-speech tasks. They consist of a noising process destroying the data and a backward stage defined as the time-reversal of the noising diffusion. Building on their success, diffusion models have recently been extended to the Riemannian manifold setting. Yet, these Riemannian diffusion models require geodesics to be defined for all times. While this setting encompasses many important applications, it does not include manifolds defined via a set of inequality constraints, which are ubiquitous in many scientific domains such as robotics and protein design. In this work, we introduce two methods to bridge this gap. First, we design a noising process based on the logarithmic barrier metric induced by the inequality constraints. Second, we introduce a noising process based on the reflected Brownian motion. As existing diffusion model techniques cannot be applied in this setting, we derive new tools to define such models in our framework. We empirically demonstrate the applicability of our methods to a number of synthetic and real-world tasks, including the constrained conformational modelling of protein backbones and robotic arms.

Spectral Diffusion Processes

Score-based generative modelling (SGM) has proven to be a very effective method for modelling densities on finite-dimensional spaces. In this work we propose to extend this methodology to learn generative models over functional spaces. To do so, we represent functional data in spectral space to dissociate the stochastic part of the processes from their space-time part. Using dimensionality reduction techniques we then sample from their stochastic component using finite dimensional SGM. We demonstrate our method's effectiveness for modelling various multimodal datasets.

Riemannian Diffusion Schrödinger Bridge

Score-based generative models exhibit state of the art performance on density estimation and generative modeling tasks. These models typically assume that the data geometry is flat, yet recent extensions have been developed to synthesize data living on Riemannian manifolds. Existing methods to accelerate sampling of diffusion models are typically not applicable in the Riemannian setting and Riemannian score-based methods have not yet been adapted to the important task of interpolation of datasets. To overcome these issues, we introduce \emph{Riemannian Diffusion Schr\"odinger Bridge}. Our proposed method generalizes Diffusion Schr\"odinger Bridge introduced in \cite{debortoli2021neurips} to the non-Euclidean setting and extends Riemannian score-based models beyond the first time reversal. We validate our proposed method on synthetic data and real Earth and climate data.

Riemannian Score-Based Generative Modeling

Score-based generative models (SGMs) are a novel class of generative models demonstrating remarkable empirical performance. One uses a diffusion to add progressively Gaussian noise to the data, while the generative model is a "denoising" process obtained by approximating the time-reversal of this "noising" diffusion. However, current SGMs make the underlying assumption that the data is supported on a Euclidean manifold with flat geometry. This prevents the use of these models for applications in robotics, geoscience or protein modeling which rely on distributions defined on Riemannian manifolds. To overcome this issue, we introduce Riemannian Score-based Generative Models (RSGMs) which extend current SGMs to the setting of compact Riemannian manifolds. We illustrate our approach with earth and climate science data and show how RSGMs can be accelerated by solving a Schr\"odinger bridge problem on manifolds.

Vector-valued Gaussian Processes on Riemannian Manifolds via Gauge Independent Projected Kernels

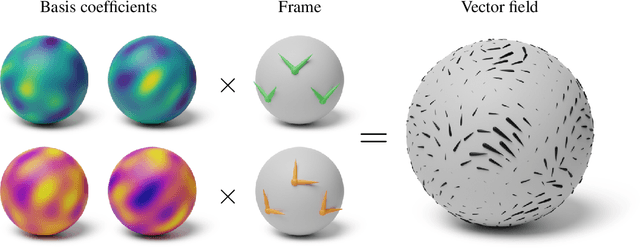
Gaussian processes are machine learning models capable of learning unknown functions in a way that represents uncertainty, thereby facilitating construction of optimal decision-making systems. Motivated by a desire to deploy Gaussian processes in novel areas of science, a rapidly-growing line of research has focused on constructively extending these models to handle non-Euclidean domains, including Riemannian manifolds, such as spheres and tori. We propose techniques that generalize this class to model vector fields on Riemannian manifolds, which are important in a number of application areas in the physical sciences. To do so, we present a general recipe for constructing gauge independent kernels, which induce Gaussian vector fields, i.e. vector-valued Gaussian processes coherent with geometry, from scalar-valued Riemannian kernels. We extend standard Gaussian process training methods, such as variational inference, to this setting. This enables vector-valued Gaussian processes on Riemannian manifolds to be trained using standard methods and makes them accessible to machine learning practitioners.

LieTransformer: Equivariant self-attention for Lie Groups

Group equivariant neural networks are used as building blocks of group invariant neural networks, which have been shown to improve generalisation performance and data efficiency through principled parameter sharing. Such works have mostly focused on group equivariant convolutions, building on the result that group equivariant linear maps are necessarily convolutions. In this work, we extend the scope of the literature to non-linear neural network modules, namely self-attention, that is emerging as a prominent building block of deep learning models. We propose the LieTransformer, an architecture composed of LieSelfAttention layers that are equivariant to arbitrary Lie groups and their discrete subgroups. We demonstrate the generality of our approach by showing experimental results that are competitive to baseline methods on a wide range of tasks: shape counting on point clouds, molecular property regression and modelling particle trajectories under Hamiltonian dynamics.

Equivariant Conditional Neural Processes

We introduce Equivariant Conditional Neural Processes (EquivCNPs), a new member of the Neural Process family that models vector-valued data in an equivariant manner with respect to isometries of $\mathbb{R}^n$. In addition, we look at multi-dimensional Gaussian Processes (GPs) under the perspective of equivariance and find the sufficient and necessary constraints to ensure a GP over $\mathbb{R}^n$ is equivariant. We test EquivCNPs on the inference of vector fields using Gaussian process samples and real-world weather data. We observe that our model significantly improves the performance of previous models. By imposing equivariance as constraints, the parameter and data efficiency of these models are increased. Moreover, we find that EquivCNPs are more robust against overfitting to local conditions of the training data.

Differentially Private Federated Variational Inference

In many real-world applications of machine learning, data are distributed across many clients and cannot leave the devices they are stored on. Furthermore, each client's data, computational resources and communication constraints may be very different. This setting is known as federated learning, in which privacy is a key concern. Differential privacy is commonly used to provide mathematical privacy guarantees. This work, to the best of our knowledge, is the first to consider federated, differentially private, Bayesian learning. We build on Partitioned Variational Inference (PVI) which was recently developed to support approximate Bayesian inference in the federated setting. We modify the client-side optimisation of PVI to provide an (${\epsilon}$, ${\delta}$)-DP guarantee. We show that it is possible to learn moderately private logistic regression models in the federated setting that achieve similar performance to models trained non-privately on centralised data.