Count Bridges enable Modeling and Deconvolving Transcriptomic Data

Many modern biological assays, including RNA sequencing, yield integer-valued counts that reflect the number of molecules detected. These measurements are often not at the desired resolution: while the unit of interest is typically a single cell, many measurement technologies produce counts aggregated over sets of cells. Although recent generative frameworks such as diffusion and flow matching have been extended to non-Euclidean and discrete settings, it remains unclear how best to model integer-valued data or how to systematically deconvolve aggregated observations. We introduce Count Bridges, a stochastic bridge process on the integers that provides an exact, tractable analogue of diffusion-style models for count data, with closed-form conditionals for efficient training and sampling. We extend this framework to enable direct training from aggregated measurements via an Expectation-Maximization-style approach that treats unit-level counts as latent variables. We demonstrate state-of-the-art performance on integer distribution matching benchmarks, comparing against flow matching and discrete flow matching baselines across various metrics. We then apply Count Bridges to two large-scale problems in biology: modeling single-cell gene expression data at the nucleotide resolution, with applications to deconvolving bulk RNA-seq, and resolving multicellular spatial transcriptomic spots into single-cell count profiles. Our methods offer a principled foundation for generative modeling and deconvolution of biological count data across scales and modalities.

Distribution-Conditioned Transport

Learning a transport model that maps a source distribution to a target distribution is a canonical problem in machine learning, but scientific applications increasingly require models that can generalize to source and target distributions unseen during training. We introduce distribution-conditioned transport (DCT), a framework that conditions transport maps on learned embeddings of source and target distributions, enabling generalization to unseen distribution pairs. DCT also allows semi-supervised learning for distributional forecasting problems: because it learns from arbitrary distribution pairs, it can leverage distributions observed at only one condition to improve transport prediction. DCT is agnostic to the underlying transport mechanism, supporting models ranging from flow matching to distributional divergence-based models (e.g. Wasserstein, MMD). We demonstrate the practical performance benefits of DCT on synthetic benchmarks and four applications in biology: batch effect transfer in single-cell genomics, perturbation prediction from mass cytometry data, learning clonal transcriptional dynamics in hematopoiesis, and modeling T-cell receptor sequence evolution.

Generative Distribution Embeddings

Many real-world problems require reasoning across multiple scales, demanding models which operate not on single data points, but on entire distributions. We introduce generative distribution embeddings (GDE), a framework that lifts autoencoders to the space of distributions. In GDEs, an encoder acts on sets of samples, and the decoder is replaced by a generator which aims to match the input distribution. This framework enables learning representations of distributions by coupling conditional generative models with encoder networks which satisfy a criterion we call distributional invariance. We show that GDEs learn predictive sufficient statistics embedded in the Wasserstein space, such that latent GDE distances approximately recover the $W_2$ distance, and latent interpolation approximately recovers optimal transport trajectories for Gaussian and Gaussian mixture distributions. We systematically benchmark GDEs against existing approaches on synthetic datasets, demonstrating consistently stronger performance. We then apply GDEs to six key problems in computational biology: learning representations of cell populations from lineage-tracing data (150K cells), predicting perturbation effects on single-cell transcriptomes (1M cells), predicting perturbation effects on cellular phenotypes (20M single-cell images), modeling tissue-specific DNA methylation patterns (253M sequences), designing synthetic yeast promoters (34M sequences), and spatiotemporal modeling of viral protein sequences (1M sequences).

The Fragility of Fairness: Causal Sensitivity Analysis for Fair Machine Learning

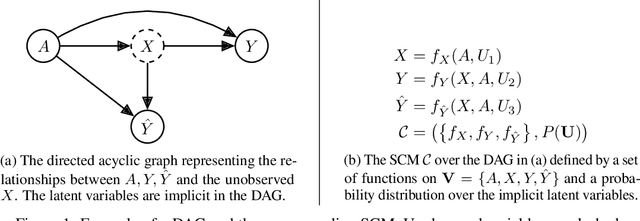
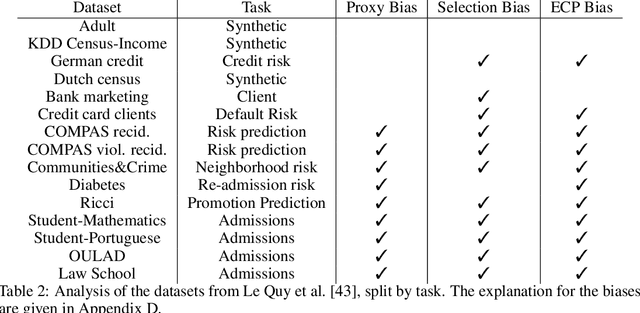
Fairness metrics are a core tool in the fair machine learning literature (FairML), used to determine that ML models are, in some sense, "fair". Real-world data, however, are typically plagued by various measurement biases and other violated assumptions, which can render fairness assessments meaningless. We adapt tools from causal sensitivity analysis to the FairML context, providing a general framework which (1) accommodates effectively any combination of fairness metric and bias that can be posed in the "oblivious setting"; (2) allows researchers to investigate combinations of biases, resulting in non-linear sensitivity; and (3) enables flexible encoding of domain-specific constraints and assumptions. Employing this framework, we analyze the sensitivity of the most common parity metrics under 3 varieties of classifier across 14 canonical fairness datasets. Our analysis reveals the striking fragility of fairness assessments to even minor dataset biases. We show that causal sensitivity analysis provides a powerful and necessary toolkit for gauging the informativeness of parity metric evaluations. Our repository is available here: https://github.com/Jakefawkes/fragile_fair.

Metropolis Sampling for Constrained Diffusion Models

Denoising diffusion models have recently emerged as the predominant paradigm for generative modelling. Their extension to Riemannian manifolds has facilitated their application to an array of problems in the natural sciences. Yet, in many practical settings, such manifolds are defined by a set of constraints and are not covered by the existing (Riemannian) diffusion model methodology. Recent work has attempted to address this issue by employing novel noising processes based on logarithmic barrier methods or reflected Brownian motions. However, the associated samplers are computationally burdensome as the complexity of the constraints increases. In this paper, we introduce an alternative simple noising scheme based on Metropolis sampling that affords substantial gains in computational efficiency and empirical performance compared to the earlier samplers. Of independent interest, we prove that this new process corresponds to a valid discretisation of the reflected Brownian motion. We demonstrate the scalability and flexibility of our approach on a range of problem settings with convex and non-convex constraints, including applications from geospatial modelling, robotics and protein design.

Diffusion Models for Constrained Domains

Denoising diffusion models are a recent class of generative models which achieve state-of-the-art results in many domains such as unconditional image generation and text-to-speech tasks. They consist of a noising process destroying the data and a backward stage defined as the time-reversal of the noising diffusion. Building on their success, diffusion models have recently been extended to the Riemannian manifold setting. Yet, these Riemannian diffusion models require geodesics to be defined for all times. While this setting encompasses many important applications, it does not include manifolds defined via a set of inequality constraints, which are ubiquitous in many scientific domains such as robotics and protein design. In this work, we introduce two methods to bridge this gap. First, we design a noising process based on the logarithmic barrier metric induced by the inequality constraints. Second, we introduce a noising process based on the reflected Brownian motion. As existing diffusion model techniques cannot be applied in this setting, we derive new tools to define such models in our framework. We empirically demonstrate the applicability of our methods to a number of synthetic and real-world tasks, including the constrained conformational modelling of protein backbones and robotic arms.

Should attention be all we need? The epistemic and ethical implications of unification in machine learning

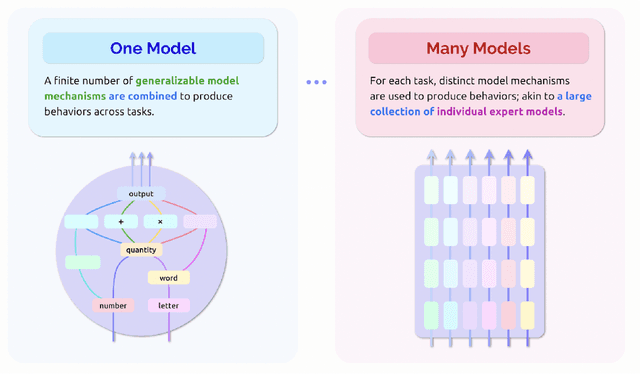
"Attention is all you need" has become a fundamental precept in machine learning research. Originally designed for machine translation, transformers and the attention mechanisms that underpin them now find success across many problem domains. With the apparent domain-agnostic success of transformers, many researchers are excited that similar model architectures can be successfully deployed across diverse applications in vision, language and beyond. We consider the benefits and risks of these waves of unification on both epistemic and ethical fronts. On the epistemic side, we argue that many of the arguments in favor of unification in the natural sciences fail to transfer over to the machine learning case, or transfer over only under assumptions that might not hold. Unification also introduces epistemic risks related to portability, path dependency, methodological diversity, and increased black-boxing. On the ethical side, we discuss risks emerging from epistemic concerns, further marginalizing underrepresented perspectives, the centralization of power, and having fewer models across more domains of application