Deep MMD Gradient Flow without adversarial training

We propose a gradient flow procedure for generative modeling by transporting particles from an initial source distribution to a target distribution, where the gradient field on the particles is given by a noise-adaptive Wasserstein Gradient of the Maximum Mean Discrepancy (MMD). The noise-adaptive MMD is trained on data distributions corrupted by increasing levels of noise, obtained via a forward diffusion process, as commonly used in denoising diffusion probabilistic models. The result is a generalization of MMD Gradient Flow, which we call Diffusion-MMD-Gradient Flow or DMMD. The divergence training procedure is related to discriminator training in Generative Adversarial Networks (GAN), but does not require adversarial training. We obtain competitive empirical performance in unconditional image generation on CIFAR10, MNIST, CELEB-A (64 x64) and LSUN Church (64 x 64). Furthermore, we demonstrate the validity of the approach when MMD is replaced by a lower bound on the KL divergence.

Dynamical Regimes of Diffusion Models

Using statistical physics methods, we study generative diffusion models in the regime where the dimension of space and the number of data are large, and the score function has been trained optimally. Our analysis reveals three distinct dynamical regimes during the backward generative diffusion process. The generative dynamics, starting from pure noise, encounters first a 'speciation' transition where the gross structure of data is unraveled, through a mechanism similar to symmetry breaking in phase transitions. It is followed at later time by a 'collapse' transition where the trajectories of the dynamics become attracted to one of the memorized data points, through a mechanism which is similar to the condensation in a glass phase. For any dataset, the speciation time can be found from a spectral analysis of the correlation matrix, and the collapse time can be found from the estimation of an 'excess entropy' in the data. The dependence of the collapse time on the dimension and number of data provides a thorough characterization of the curse of dimensionality for diffusion models. Analytical solutions for simple models like high-dimensional Gaussian mixtures substantiate these findings and provide a theoretical framework, while extensions to more complex scenarios and numerical validations with real datasets confirm the theoretical predictions.

Particle Guidance: non-I.I.D. Diverse Sampling with Diffusion Models

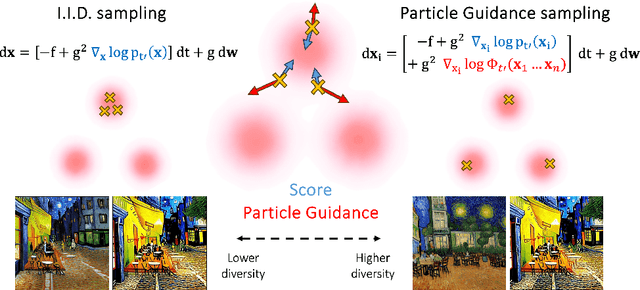
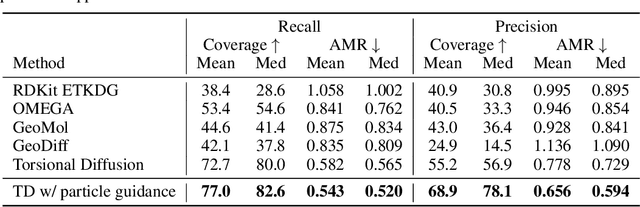
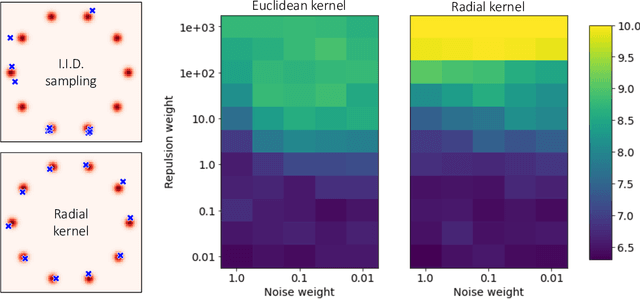
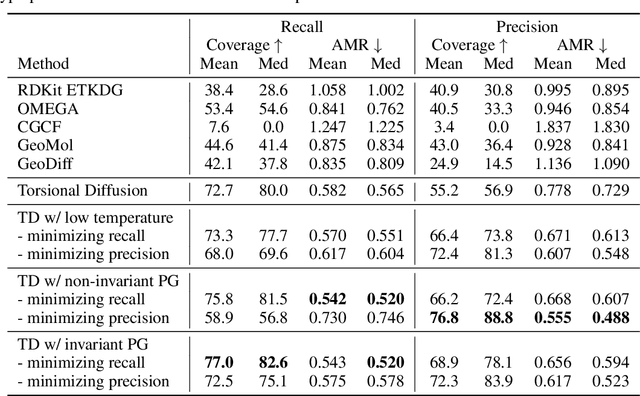
In light of the widespread success of generative models, a significant amount of research has gone into speeding up their sampling time. However, generative models are often sampled multiple times to obtain a diverse set incurring a cost that is orthogonal to sampling time. We tackle the question of how to improve diversity and sample efficiency by moving beyond the common assumption of independent samples. We propose particle guidance, an extension of diffusion-based generative sampling where a joint-particle time-evolving potential enforces diversity. We analyze theoretically the joint distribution that particle guidance generates, its implications on the choice of potential, and the connections with methods in other disciplines. Empirically, we test the framework both in the setting of conditional image generation, where we are able to increase diversity without affecting quality, and molecular conformer generation, where we reduce the state-of-the-art median error by 13% on average.

Plug-and-Play Posterior Sampling under Mismatched Measurement and Prior Models

Posterior sampling has been shown to be a powerful Bayesian approach for solving imaging inverse problems. The recent plug-and-play unadjusted Langevin algorithm (PnP-ULA) has emerged as a promising method for Monte Carlo sampling and minimum mean squared error (MMSE) estimation by combining physical measurement models with deep-learning priors specified using image denoisers. However, the intricate relationship between the sampling distribution of PnP-ULA and the mismatched data-fidelity and denoiser has not been theoretically analyzed. We address this gap by proposing a posterior-L2 pseudometric and using it to quantify an explicit error bound for PnP-ULA under mismatched posterior distribution. We numerically validate our theory on several inverse problems such as sampling from Gaussian mixture models and image deblurring. Our results suggest that the sensitivity of the sampling distribution of PnP-ULA to a mismatch in the measurement model and the denoiser can be precisely characterized.

Metropolis Sampling for Constrained Diffusion Models

Denoising diffusion models have recently emerged as the predominant paradigm for generative modelling. Their extension to Riemannian manifolds has facilitated their application to an array of problems in the natural sciences. Yet, in many practical settings, such manifolds are defined by a set of constraints and are not covered by the existing (Riemannian) diffusion model methodology. Recent work has attempted to address this issue by employing novel noising processes based on logarithmic barrier methods or reflected Brownian motions. However, the associated samplers are computationally burdensome as the complexity of the constraints increases. In this paper, we introduce an alternative simple noising scheme based on Metropolis sampling that affords substantial gains in computational efficiency and empirical performance compared to the earlier samplers. Of independent interest, we prove that this new process corresponds to a valid discretisation of the reflected Brownian motion. We demonstrate the scalability and flexibility of our approach on a range of problem settings with convex and non-convex constraints, including applications from geospatial modelling, robotics and protein design.

Can Push-forward Generative Models Fit Multimodal Distributions?

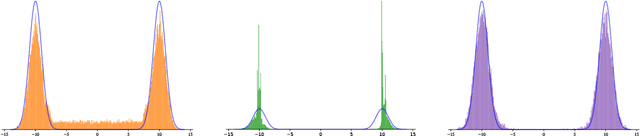
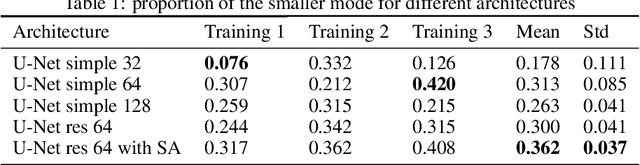
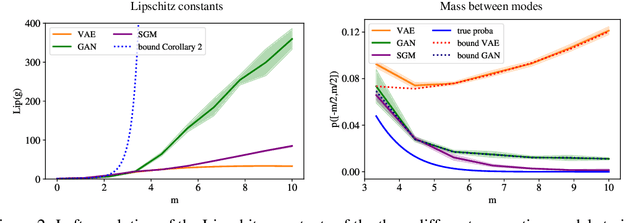
Many generative models synthesize data by transforming a standard Gaussian random variable using a deterministic neural network. Among these models are the Variational Autoencoders and the Generative Adversarial Networks. In this work, we call them "push-forward" models and study their expressivity. We show that the Lipschitz constant of these generative networks has to be large in order to fit multimodal distributions. More precisely, we show that the total variation distance and the Kullback-Leibler divergence between the generated and the data distribution are bounded from below by a constant depending on the mode separation and the Lipschitz constant. Since constraining the Lipschitz constants of neural networks is a common way to stabilize generative models, there is a provable trade-off between the ability of push-forward models to approximate multimodal distributions and the stability of their training. We validate our findings on one-dimensional and image datasets and empirically show that generative models consisting of stacked networks with stochastic input at each step, such as diffusion models do not suffer of such limitations.

On Maximum-a-Posteriori estimation with Plug & Play priors and stochastic gradient descent

Bayesian methods to solve imaging inverse problems usually combine an explicit data likelihood function with a prior distribution that explicitly models expected properties of the solution. Many kinds of priors have been explored in the literature, from simple ones expressing local properties to more involved ones exploiting image redundancy at a non-local scale. In a departure from explicit modelling, several recent works have proposed and studied the use of implicit priors defined by an image denoising algorithm. This approach, commonly known as Plug & Play (PnP) regularisation, can deliver remarkably accurate results, particularly when combined with state-of-the-art denoisers based on convolutional neural networks. However, the theoretical analysis of PnP Bayesian models and algorithms is difficult and works on the topic often rely on unrealistic assumptions on the properties of the image denoiser. This papers studies maximum-a-posteriori (MAP) estimation for Bayesian models with PnP priors. We first consider questions related to existence, stability and well-posedness, and then present a convergence proof for MAP computation by PnP stochastic gradient descent (PnP-SGD) under realistic assumptions on the denoiser used. We report a range of imaging experiments demonstrating PnP-SGD as well as comparisons with other PnP schemes.

Bayesian imaging using Plug & Play priors: when Langevin meets Tweedie

Since the seminal work of Venkatakrishnan et al. (2013), Plug & Play (PnP) methods have become ubiquitous in Bayesian imaging. These methods derive Minimum Mean Square Error (MMSE) or Maximum A Posteriori (MAP) estimators for inverse problems in imaging by combining an explicit likelihood function with a prior that is implicitly defined by an image denoising algorithm. The PnP algorithms proposed in the literature mainly differ in the iterative schemes they use for optimisation or for sampling. In the case of optimisation schemes, some recent works guarantee the convergence to a fixed point, albeit not necessarily a MAP estimate. In the case of sampling schemes, to the best of our knowledge, there is no known proof of convergence. There also remain important open questions regarding whether the underlying Bayesian models and estimators are well defined, well-posed, and have the basic regularity properties required to support these numerical schemes. To address these limitations, this paper develops theory, methods, and provably convergent algorithms for performing Bayesian inference with PnP priors. We introduce two algorithms: 1) PnP-ULA (Unadjusted Langevin Algorithm) for Monte Carlo sampling and MMSE inference; and 2) PnP-SGD (Stochastic Gradient Descent) for MAP inference. Using recent results on the quantitative convergence of Markov chains, we establish detailed convergence guarantees for these two algorithms under realistic assumptions on the denoising operators used, with special attention to denoisers based on deep neural networks. We also show that these algorithms approximately target a decision-theoretically optimal Bayesian model that is well-posed. The proposed algorithms are demonstrated on several canonical problems such as image deblurring, inpainting, and denoising, where they are used for point estimation as well as for uncertainty visualisation and quantification.