On the role of non-linear latent features in bipartite generative neural networks

We investigate the phase diagram and memory retrieval capabilities of bipartite energy-based neural networks, namely Restricted Boltzmann Machines (RBMs), as a function of the prior distribution imposed on their hidden units - including binary, multi-state, and ReLU-like activations. Drawing connections to the Hopfield model and employing analytical tools from statistical physics of disordered systems, we explore how the architectural choices and activation functions shape the thermodynamic properties of these models. Our analysis reveals that standard RBMs with binary hidden nodes and extensive connectivity suffer from reduced critical capacity, limiting their effectiveness as associative memories. To address this, we examine several modifications, such as introducing local biases and adopting richer hidden unit priors. These adjustments restore ordered retrieval phases and markedly improve recall performance, even at finite temperatures. Our theoretical findings, supported by finite-size Monte Carlo simulations, highlight the importance of hidden unit design in enhancing the expressive power of RBMs.

Why Diffusion Models Don't Memorize: The Role of Implicit Dynamical Regularization in Training

Diffusion models have achieved remarkable success across a wide range of generative tasks. A key challenge is understanding the mechanisms that prevent their memorization of training data and allow generalization. In this work, we investigate the role of the training dynamics in the transition from generalization to memorization. Through extensive experiments and theoretical analysis, we identify two distinct timescales: an early time $\tau_\mathrm{gen}$ at which models begin to generate high-quality samples, and a later time $\tau_\mathrm{mem}$ beyond which memorization emerges. Crucially, we find that $\tau_\mathrm{mem}$ increases linearly with the training set size $n$, while $\tau_\mathrm{gen}$ remains constant. This creates a growing window of training times with $n$ where models generalize effectively, despite showing strong memorization if training continues beyond it. It is only when $n$ becomes larger than a model-dependent threshold that overfitting disappears at infinite training times. These findings reveal a form of implicit dynamical regularization in the training dynamics, which allow to avoid memorization even in highly overparameterized settings. Our results are supported by numerical experiments with standard U-Net architectures on realistic and synthetic datasets, and by a theoretical analysis using a tractable random features model studied in the high-dimensional limit.

From Zero to Hero: How local curvature at artless initial conditions leads away from bad minima

We investigate the optimization dynamics of gradient descent in a non-convex and high-dimensional setting, with a focus on the phase retrieval problem as a case study for complex loss landscapes. We first study the high-dimensional limit where both the number $M$ and the dimension $N$ of the data are going to infinity at fixed signal-to-noise ratio $\alpha = M/N$. By analyzing how the local curvature changes during optimization, we uncover that for intermediate $\alpha$, the Hessian displays a downward direction pointing towards good minima in the first regime of the descent, before being trapped in bad minima at the end. Hence, the local landscape is benign and informative at first, before gradient descent brings the system into a uninformative maze. The transition between the two regimes is associated to a BBP-type threshold in the time-dependent Hessian. Through both theoretical analysis and numerical experiments, we show that in practical cases, i.e. for finite but even very large $N$, successful optimization via gradient descent in phase retrieval is achieved by falling towards the good minima before reaching the bad ones. This mechanism explains why successful recovery is obtained well before the algorithmic transition corresponding to the high-dimensional limit. Technically, this is associated to strong logarithmic corrections of the algorithmic transition at large $N$ with respect to the one expected in the $N\to\infty$ limit. Our analysis sheds light on such a new mechanism that facilitate gradient descent dynamics in finite large dimensions, also highlighting the importance of good initialization of spectral properties for optimization in complex high-dimensional landscapes.

Dynamical Regimes of Diffusion Models

Using statistical physics methods, we study generative diffusion models in the regime where the dimension of space and the number of data are large, and the score function has been trained optimally. Our analysis reveals three distinct dynamical regimes during the backward generative diffusion process. The generative dynamics, starting from pure noise, encounters first a 'speciation' transition where the gross structure of data is unraveled, through a mechanism similar to symmetry breaking in phase transitions. It is followed at later time by a 'collapse' transition where the trajectories of the dynamics become attracted to one of the memorized data points, through a mechanism which is similar to the condensation in a glass phase. For any dataset, the speciation time can be found from a spectral analysis of the correlation matrix, and the collapse time can be found from the estimation of an 'excess entropy' in the data. The dependence of the collapse time on the dimension and number of data provides a thorough characterization of the curse of dimensionality for diffusion models. Analytical solutions for simple models like high-dimensional Gaussian mixtures substantiate these findings and provide a theoretical framework, while extensions to more complex scenarios and numerical validations with real datasets confirm the theoretical predictions.

Regularization of Mixture Models for Robust Principal Graph Learning

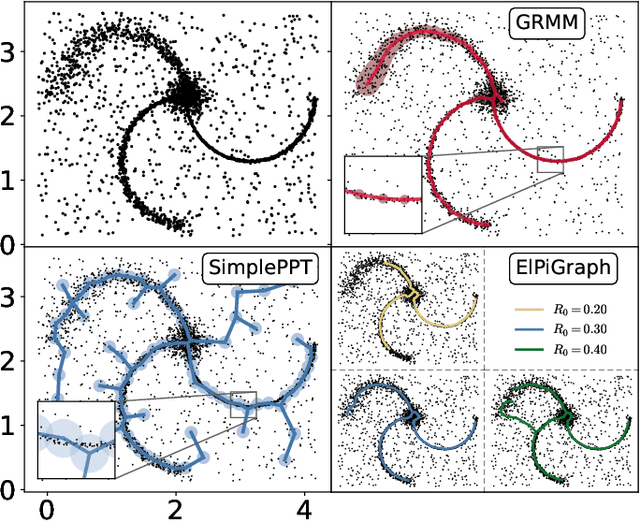
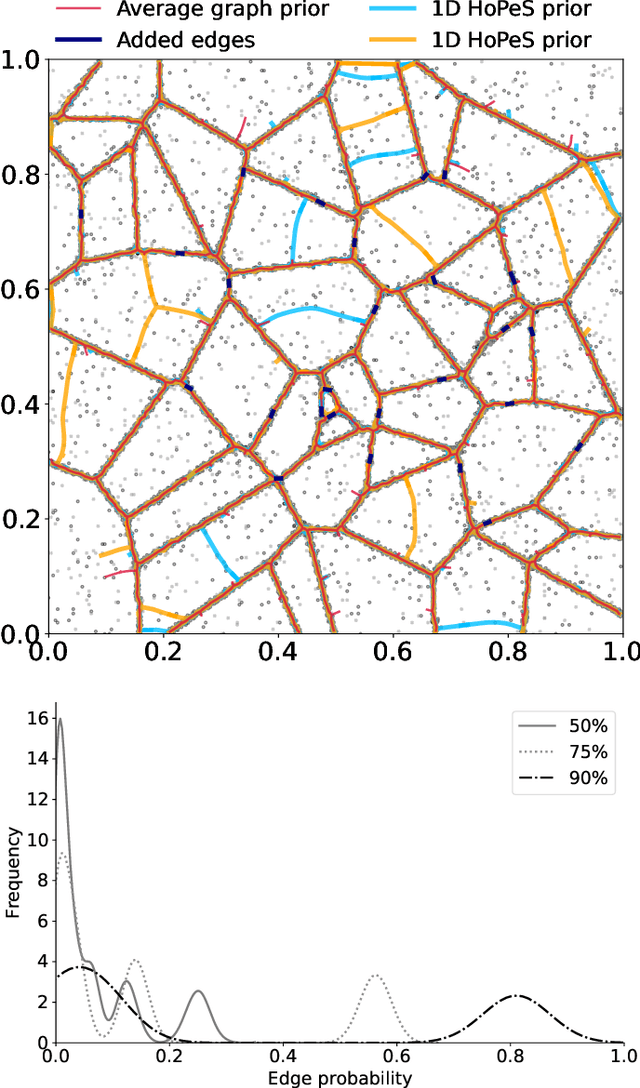
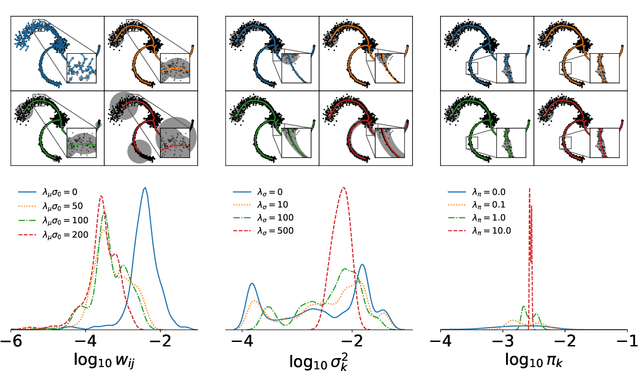
A regularized version of Mixture Models is proposed to learn a principal graph from a distribution of $D$-dimensional data points. In the particular case of manifold learning for ridge detection, we assume that the underlying manifold can be modeled as a graph structure acting like a topological prior for the Gaussian clusters turning the problem into a maximum a posteriori estimation. Parameters of the model are iteratively estimated through an Expectation-Maximization procedure making the learning of the structure computationally efficient with guaranteed convergence for any graph prior in a polynomial time. We also embed in the formalism a natural way to make the algorithm robust to outliers of the pattern and heteroscedasticity of the manifold sampling coherently with the graph structure. The method uses a graph prior given by the minimum spanning tree that we extend using random sub-samplings of the dataset to take into account cycles that can be observed in the spatial distribution.