On the role of non-linear latent features in bipartite generative neural networks

We investigate the phase diagram and memory retrieval capabilities of bipartite energy-based neural networks, namely Restricted Boltzmann Machines (RBMs), as a function of the prior distribution imposed on their hidden units - including binary, multi-state, and ReLU-like activations. Drawing connections to the Hopfield model and employing analytical tools from statistical physics of disordered systems, we explore how the architectural choices and activation functions shape the thermodynamic properties of these models. Our analysis reveals that standard RBMs with binary hidden nodes and extensive connectivity suffer from reduced critical capacity, limiting their effectiveness as associative memories. To address this, we examine several modifications, such as introducing local biases and adopting richer hidden unit priors. These adjustments restore ordered retrieval phases and markedly improve recall performance, even at finite temperatures. Our theoretical findings, supported by finite-size Monte Carlo simulations, highlight the importance of hidden unit design in enhancing the expressive power of RBMs.

A theoretical framework for overfitting in energy-based modeling

We investigate the impact of limited data on training pairwise energy-based models for inverse problems aimed at identifying interaction networks. Utilizing the Gaussian model as testbed, we dissect training trajectories across the eigenbasis of the coupling matrix, exploiting the independent evolution of eigenmodes and revealing that the learning timescales are tied to the spectral decomposition of the empirical covariance matrix. We see that optimal points for early stopping arise from the interplay between these timescales and the initial conditions of training. Moreover, we show that finite data corrections can be accurately modeled through asymptotic random matrix theory calculations and provide the counterpart of generalized cross-validation in the energy based model context. Our analytical framework extends to binary-variable maximum-entropy pairwise models with minimal variations. These findings offer strategies to control overfitting in discrete-variable models through empirical shrinkage corrections, improving the management of overfitting in energy-based generative models.

The Copycat Perceptron: Smashing Barriers Through Collective Learning

We characterize the equilibrium properties of a model of $y$ coupled binary perceptrons in the teacher-student scenario, subject to a suitable learning rule, with an explicit ferromagnetic coupling proportional to the Hamming distance between the students' weights. In contrast to recent works, we analyze a more general setting in which a thermal noise is present that affects the generalization performance of each student. Specifically, in the presence of a nonzero temperature, which assigns nonzero probability to configurations that misclassify samples with respect to the teacher's prescription, we find that the coupling of replicas leads to a shift of the phase diagram to smaller values of $\alpha$: This suggests that the free energy landscape gets smoother around the solution with good generalization (i.e., the teacher) at a fixed fraction of reviewed examples, which allows local update algorithms such as Simulated Annealing to reach the solution before the dynamics gets frozen. Finally, from a learning perspective, these results suggest that more students (in this case, with the same amount of data) are able to learn the same rule when coupled together with a smaller amount of data.

Explaining the effects of non-convergent sampling in the training of Energy-Based Models

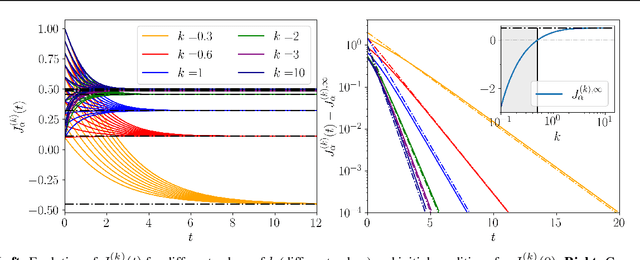
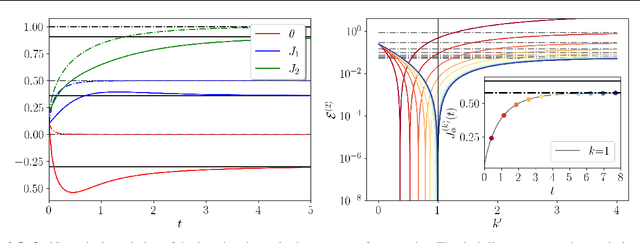
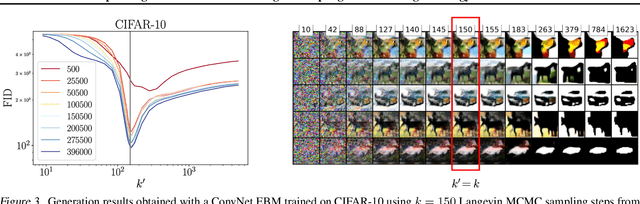
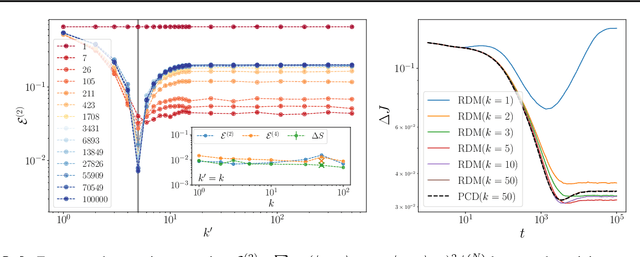
In this paper, we quantify the impact of using non-convergent Markov chains to train Energy-Based models (EBMs). In particular, we show analytically that EBMs trained with non-persistent short runs to estimate the gradient can perfectly reproduce a set of empirical statistics of the data, not at the level of the equilibrium measure, but through a precise dynamical process. Our results provide a first-principles explanation for the observations of recent works proposing the strategy of using short runs starting from random initial conditions as an efficient way to generate high-quality samples in EBMs, and lay the groundwork for using EBMs as diffusion models. After explaining this effect in generic EBMs, we analyze two solvable models in which the effect of the non-convergent sampling in the trained parameters can be described in detail. Finally, we test these predictions numerically on the Boltzmann machine.

Thermodynamics of bidirectional associative memories

In this paper we investigate the equilibrium properties of bidirectional associative memories (BAMs). Introduced by Kosko in 1988 as a generalization of the Hopfield model to a bipartite structure, the simplest architecture is defined by two layers of neurons, with synaptic connections only between units of different layers: even without internal connections within each layer, information storage and retrieval are still possible through the reverberation of neural activities passing from one layer to another. We characterize the computational capabilities of a stochastic extension of this model in the thermodynamic limit, by applying rigorous techniques from statistical physics. A detailed picture of the phase diagram at the replica symmetric level is provided, both at finite temperature and in the noiseless regime. An analytical and numerical inspection of the transition curves (namely critical lines splitting the various modes of operation of the machine) is carried out as the control parameters - noise, load and asymmetry between the two layer sizes - are tuned. In particular, with a finite asymmetry between the two layers, it is shown how the BAM can store information more efficiently than the Hopfield model by requiring less parameters to encode a fixed number of patterns. Comparisons are made with numerical simulations of neural dynamics. Finally, a low-load analysis is carried out to explain the retrieval mechanism in the BAM by analogy with two interacting Hopfield models. A potential equivalence with two coupled Restricted Boltmzann Machines is also discussed.

Inference in conditioned dynamics through causality restoration

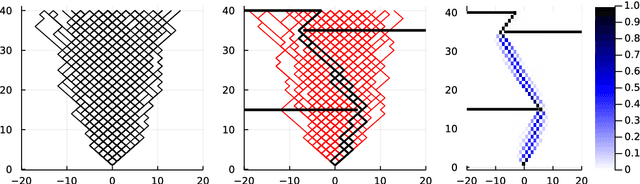
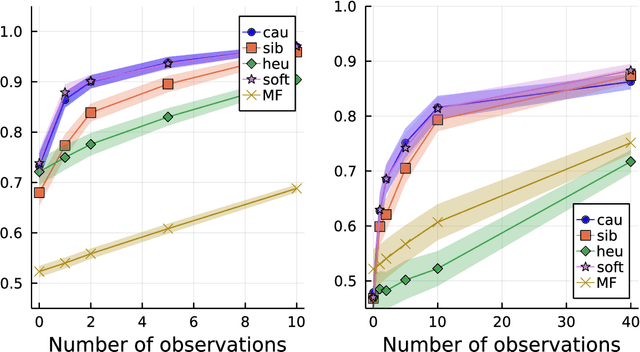
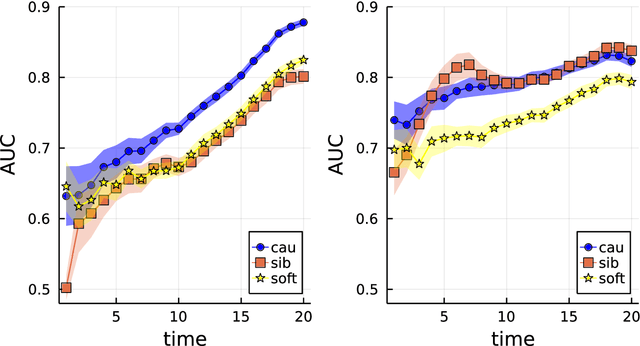
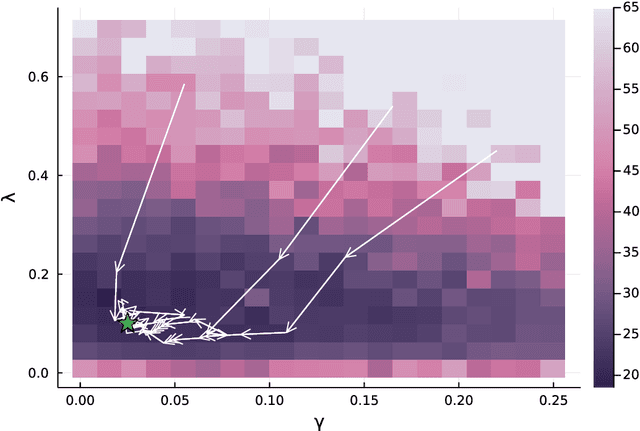
Computing observables from conditioned dynamics is typically computationally hard, because, although obtaining independent samples efficiently from the unconditioned dynamics is usually feasible, generally most of the samples must be discarded (in a form of importance sampling) because they do not satisfy the imposed conditions. Sampling directly from the conditioned distribution is non-trivial, as conditioning breaks the causal properties of the dynamics which ultimately renders the sampling procedure efficient. One standard way of achieving it is through a Metropolis Monte-Carlo procedure, but this procedure is normally slow and a very large number of Monte-Carlo steps is needed to obtain a small number of statistically independent samples. In this work, we propose an alternative method to produce independent samples from a conditioned distribution. The method learns the parameters of a generalized dynamical model that optimally describe the conditioned distribution in a variational sense. The outcome is an effective, unconditioned, dynamical model, from which one can trivially obtain independent samples, effectively restoring causality of the conditioned distribution. The consequences are twofold: on the one hand, it allows us to efficiently compute observables from the conditioned dynamics by simply averaging over independent samples. On the other hand, the method gives an effective unconditioned distribution which is easier to interpret. The method is flexible and can be applied virtually to any dynamics. We discuss an important application of the method, namely the problem of epidemic risk assessment from (imperfect) clinical tests, for a large family of time-continuous epidemic models endowed with a Gillespie-like sampler. We show that the method compares favorably against the state of the art, including the soft-margin approach and mean-field methods.

Epidemic mitigation by statistical inference from contact tracing data

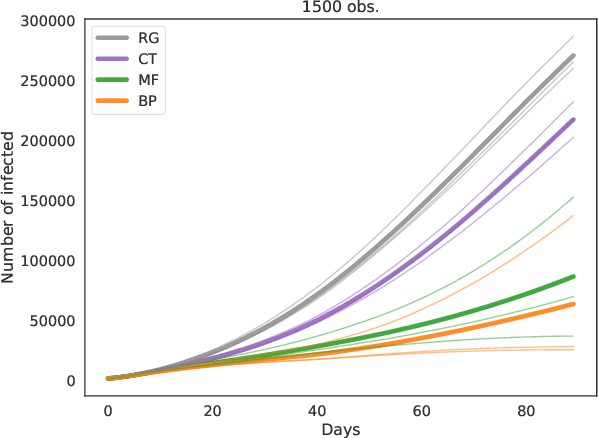
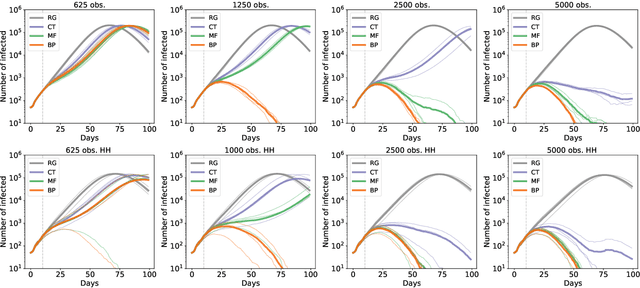
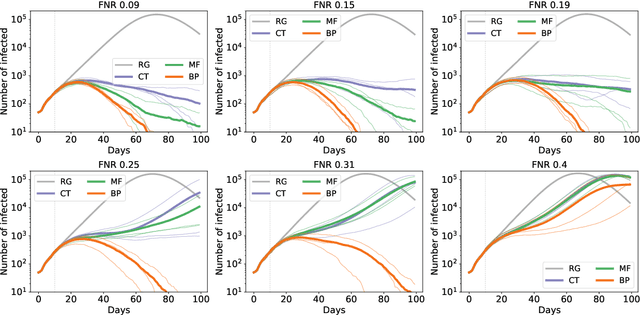
Contact-tracing is an essential tool in order to mitigate the impact of pandemic such as the COVID-19. In order to achieve efficient and scalable contact-tracing in real time, digital devices can play an important role. While a lot of attention has been paid to analyzing the privacy and ethical risks of the associated mobile applications, so far much less research has been devoted to optimizing their performance and assessing their impact on the mitigation of the epidemic. We develop Bayesian inference methods to estimate the risk that an individual is infected. This inference is based on the list of his recent contacts and their own risk levels, as well as personal information such as results of tests or presence of syndromes. We propose to use probabilistic risk estimation in order to optimize testing and quarantining strategies for the control of an epidemic. Our results show that in some range of epidemic spreading (typically when the manual tracing of all contacts of infected people becomes practically impossible, but before the fraction of infected people reaches the scale where a lock-down becomes unavoidable), this inference of individuals at risk could be an efficient way to mitigate the epidemic. Our approaches translate into fully distributed algorithms that only require communication between individuals who have recently been in contact. Such communication may be encrypted and anonymized and thus compatible with privacy preserving standards. We conclude that probabilistic risk estimation is capable to enhance performance of digital contact tracing and should be considered in the currently developed mobile applications.

Loop corrections in spin models through density consistency

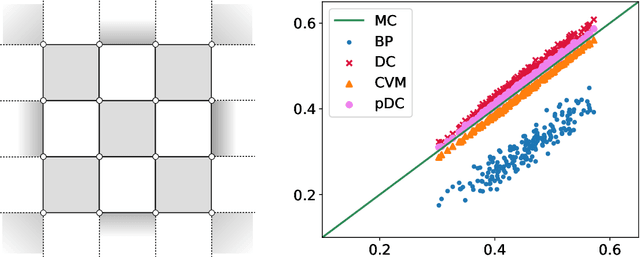
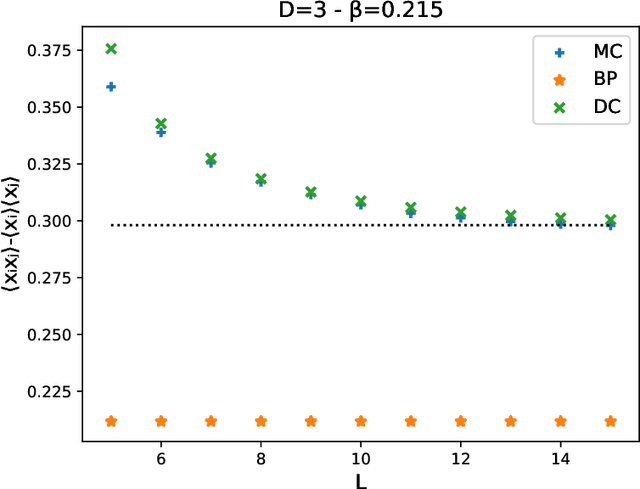
Computing marginal distributions of discrete or semi-discrete Markov Random Fields (MRF) is a fundamental, generally intractable, problem with a vast number of applications on virtually all fields of science. We present a new family of computational schemes to calculate approximately marginals of discrete MRFs. This method shares some desirable properties with Belief Propagation, in particular providing exact marginals on acyclic graphs; but at difference with it, it includes some loop corrections, i.e. it takes into account correlations coming from all cycles in the factor graph. It is also similar to Adaptive TAP, but at difference with it, the consistency is not on the first two moments of the distribution but rather on the value of its density on a subset of values. Results on random connectivity and finite dimensional Ising and Edward-Anderson models show a significant improvement with respect to the Bethe-Peierls (tree) approximation in all cases, and significant improvement with respect to Cluster Variational Method and Loop Corrected Bethe approximation in many cases. In particular, for the critical inverse temperature $\beta_{c}$ of the homogeneous hypercubic lattice, the $1/d$ expansion of $\left(d\beta_{c}\right)^{-1}$ of the proposed scheme is exact up to the $d^{-3}$ order, whereas the two latter are exact only up to the $d^{-2}$ order.