Indaco Biazzo
The autoregressive neural network architecture of the Boltzmann distribution of pairwise interacting spins systems
Feb 16, 2023Abstract:Generative Autoregressive Neural Networks (ARNN) have recently demonstrated exceptional results in image and language generation tasks, contributing to the growing popularity of generative models in both scientific and commercial applications. This work presents a physical interpretation of the ARNNs by reformulating the Boltzmann distribution of binary pairwise interacting systems into autoregressive form. The resulting ARNN architecture has weights and biases of its first layer corresponding to the Hamiltonian's couplings and external fields, featuring widely used structures like the residual connections and a recurrent architecture with clear physical meanings. However, the exponential growth, with system size, of the number of parameters of the hidden layers makes its direct application unfeasible. Nevertheless, its architecture's explicit formulation allows using statistical physics techniques to derive new ARNNs for specific systems. As examples, new effective ARNN architectures are derived from two well-known mean-field systems, the Curie-Weiss and Sherrington-Kirkpatrick models, showing superior performances in approximating the Boltzmann distributions of the corresponding physics model than other commonly used ARNNs architectures. The connection established between the physics of the system and the ARNN architecture provides a way to derive new neural network architectures for different interacting systems and interpret existing ones from a physical perspective.
Epidemic inference through generative neural networks
Nov 08, 2021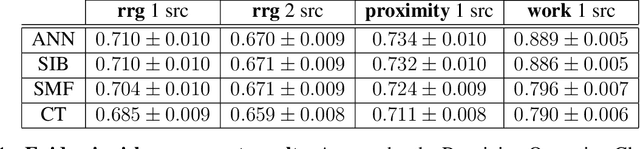


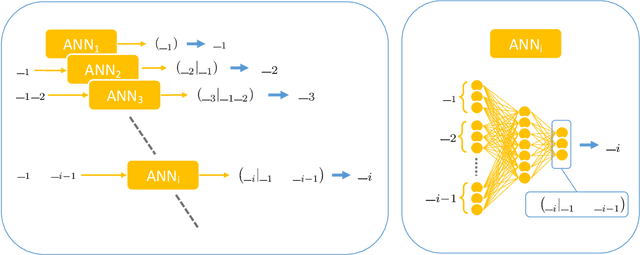
Abstract:Reconstructing missing information in epidemic spreading on contact networks can be essential in prevention and containment strategies. For instance, identifying and warning infective but asymptomatic individuals (e.g., manual contact tracing) helped contain outbreaks in the COVID-19 pandemic. The number of possible epidemic cascades typically grows exponentially with the number of individuals involved. The challenge posed by inference problems in the epidemics processes originates from the difficulty of identifying the almost negligible subset of those compatible with the evidence (for instance, medical tests). Here we present a new generative neural networks framework that can sample the most probable infection cascades compatible with observations. Moreover, the framework can infer the parameters governing the spreading of infections. The proposed method obtains better or comparable results with existing methods on the patient zero problem, risk assessment, and inference of infectious parameters in synthetic and real case scenarios like spreading infections in workplaces and hospitals.
Epidemic mitigation by statistical inference from contact tracing data
Sep 20, 2020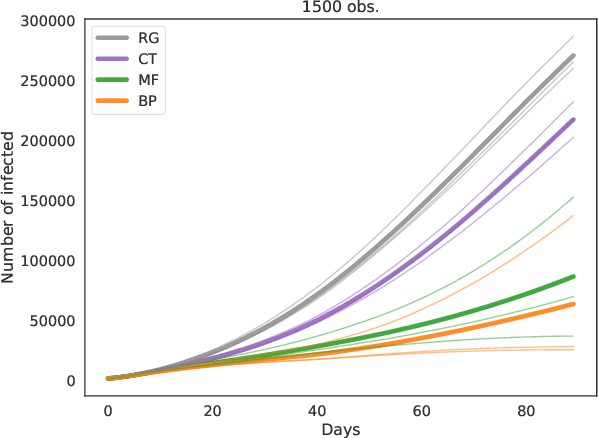
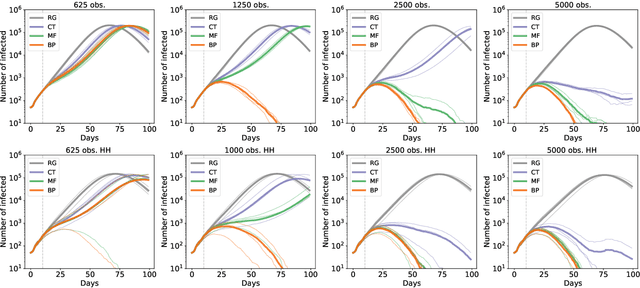
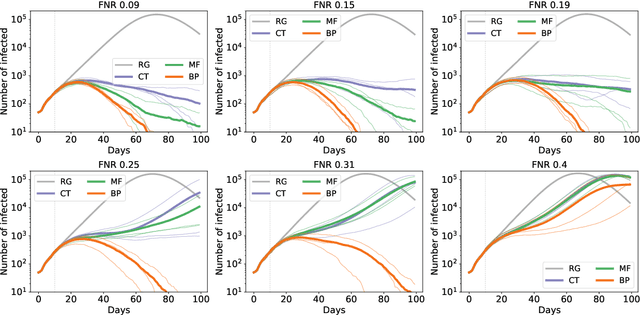

Abstract:Contact-tracing is an essential tool in order to mitigate the impact of pandemic such as the COVID-19. In order to achieve efficient and scalable contact-tracing in real time, digital devices can play an important role. While a lot of attention has been paid to analyzing the privacy and ethical risks of the associated mobile applications, so far much less research has been devoted to optimizing their performance and assessing their impact on the mitigation of the epidemic. We develop Bayesian inference methods to estimate the risk that an individual is infected. This inference is based on the list of his recent contacts and their own risk levels, as well as personal information such as results of tests or presence of syndromes. We propose to use probabilistic risk estimation in order to optimize testing and quarantining strategies for the control of an epidemic. Our results show that in some range of epidemic spreading (typically when the manual tracing of all contacts of infected people becomes practically impossible, but before the fraction of infected people reaches the scale where a lock-down becomes unavoidable), this inference of individuals at risk could be an efficient way to mitigate the epidemic. Our approaches translate into fully distributed algorithms that only require communication between individuals who have recently been in contact. Such communication may be encrypted and anonymized and thus compatible with privacy preserving standards. We conclude that probabilistic risk estimation is capable to enhance performance of digital contact tracing and should be considered in the currently developed mobile applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge