Evidence of Replica Symmetry Breaking under the Nishimori conditions in epidemic inference on graphs

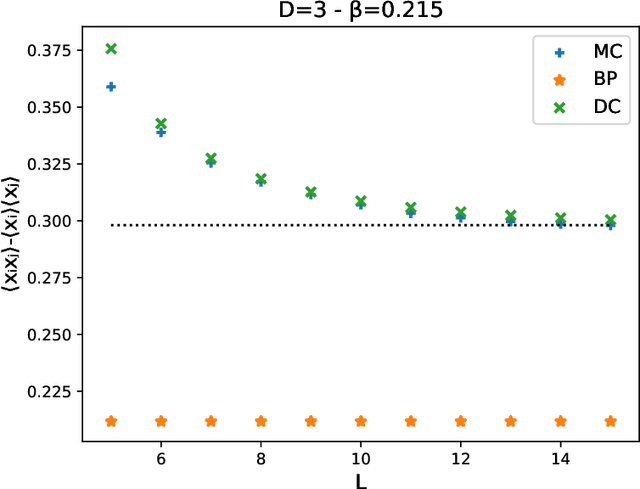
In Bayesian inference, computing the posterior distribution from the data is typically a non-trivial problem, which usually requires approximations such as mean-field approaches or numerical methods, like the Monte Carlo Markov Chain. Being a high-dimensional distribution over a set of correlated variables, the posterior distribution can undergo the notorious replica symmetry breaking transition. When it happens, several mean-field methods and virtually every Monte Carlo scheme can not provide a reasonable approximation to the posterior and its marginals. Replica symmetry is believed to be guaranteed whenever the data is generated with known prior and likelihood distributions, namely under the so-called Nishimori conditions. In this paper, we break this belief, by providing a counter-example showing that, under the Nishimori conditions, replica symmetry breaking arises. Introducing a simple, geometrical model that can be thought of as a patient zero retrieval problem in a highly infectious regime of the epidemic Susceptible-Infectious model, we show that under the Nishimori conditions, there is evidence of replica symmetry breaking. We achieve this result by computing the instability of the replica symmetric cavity method toward the one step replica symmetry broken phase. The origin of this phenomenon -- replica symmetry breaking under the Nishimori conditions -- is likely due to the correlated disorder appearing in the epidemic models.

Inference in conditioned dynamics through causality restoration

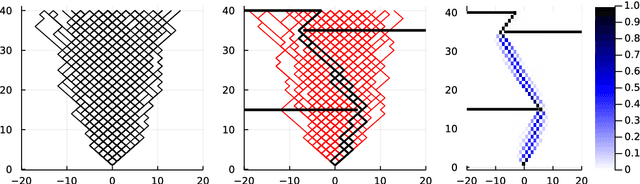
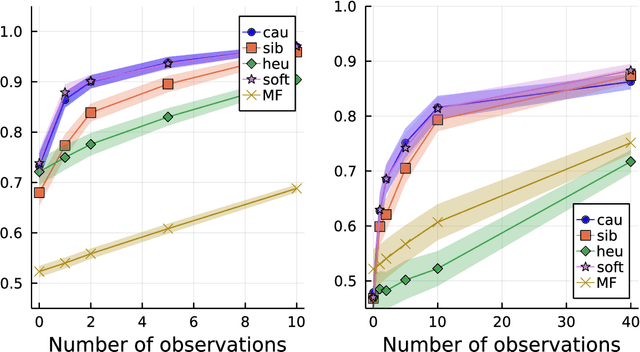
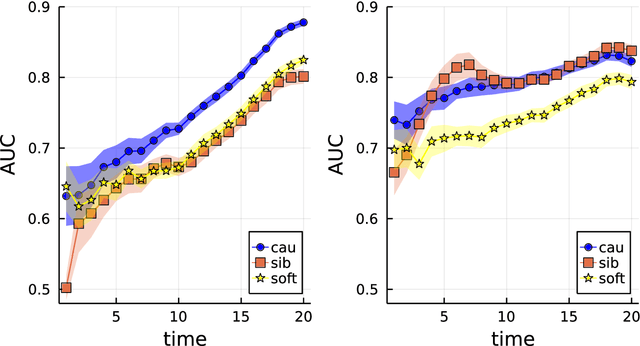
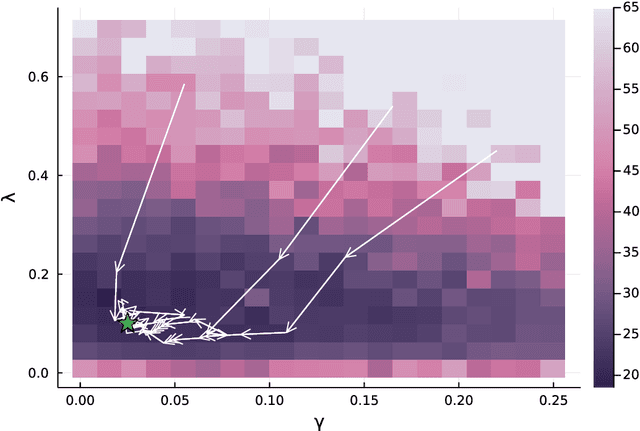
Computing observables from conditioned dynamics is typically computationally hard, because, although obtaining independent samples efficiently from the unconditioned dynamics is usually feasible, generally most of the samples must be discarded (in a form of importance sampling) because they do not satisfy the imposed conditions. Sampling directly from the conditioned distribution is non-trivial, as conditioning breaks the causal properties of the dynamics which ultimately renders the sampling procedure efficient. One standard way of achieving it is through a Metropolis Monte-Carlo procedure, but this procedure is normally slow and a very large number of Monte-Carlo steps is needed to obtain a small number of statistically independent samples. In this work, we propose an alternative method to produce independent samples from a conditioned distribution. The method learns the parameters of a generalized dynamical model that optimally describe the conditioned distribution in a variational sense. The outcome is an effective, unconditioned, dynamical model, from which one can trivially obtain independent samples, effectively restoring causality of the conditioned distribution. The consequences are twofold: on the one hand, it allows us to efficiently compute observables from the conditioned dynamics by simply averaging over independent samples. On the other hand, the method gives an effective unconditioned distribution which is easier to interpret. The method is flexible and can be applied virtually to any dynamics. We discuss an important application of the method, namely the problem of epidemic risk assessment from (imperfect) clinical tests, for a large family of time-continuous epidemic models endowed with a Gillespie-like sampler. We show that the method compares favorably against the state of the art, including the soft-margin approach and mean-field methods.

Epidemic inference through generative neural networks

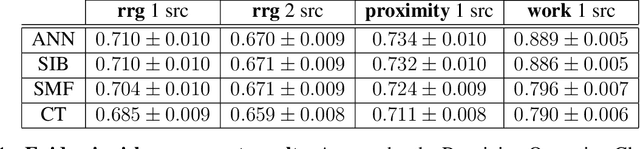
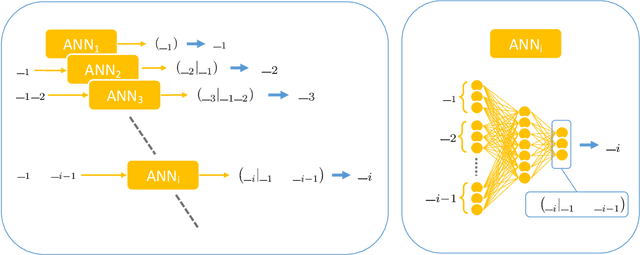
Reconstructing missing information in epidemic spreading on contact networks can be essential in prevention and containment strategies. For instance, identifying and warning infective but asymptomatic individuals (e.g., manual contact tracing) helped contain outbreaks in the COVID-19 pandemic. The number of possible epidemic cascades typically grows exponentially with the number of individuals involved. The challenge posed by inference problems in the epidemics processes originates from the difficulty of identifying the almost negligible subset of those compatible with the evidence (for instance, medical tests). Here we present a new generative neural networks framework that can sample the most probable infection cascades compatible with observations. Moreover, the framework can infer the parameters governing the spreading of infections. The proposed method obtains better or comparable results with existing methods on the patient zero problem, risk assessment, and inference of infectious parameters in synthetic and real case scenarios like spreading infections in workplaces and hospitals.

Expectation propagation for the diluted Bayesian classifier

Efficient feature selection from high-dimensional datasets is a very important challenge in many data-driven fields of science and engineering. We introduce a statistical mechanics inspired strategy that addresses the problem of sparse feature selection in the context of binary classification by leveraging a computational scheme known as expectation propagation (EP). The algorithm is used in order to train a continuous-weights perceptron learning a classification rule from a set of (possibly partly mislabeled) examples provided by a teacher perceptron with diluted continuous weights. We test the method in the Bayes optimal setting under a variety of conditions and compare it to other state-of-the-art algorithms based on message passing and on expectation maximization approximate inference schemes. Overall, our simulations show that EP is a robust and competitive algorithm in terms of variable selection properties, estimation accuracy and computationally complexity, especially when the student perceptron is trained from correlated patterns that prevent other iterative methods from converging. Furthermore, our numerical tests demonstrate that the algorithm is capable of learning online the unknown values of prior parameters, such as the dilution level of the weights of the teacher perceptron and the fraction of mislabeled examples, quite accurately. This is achieved by means of a simple maximum likelihood strategy that consists in minimizing the free energy associated with the EP algorithm.

Epidemic mitigation by statistical inference from contact tracing data

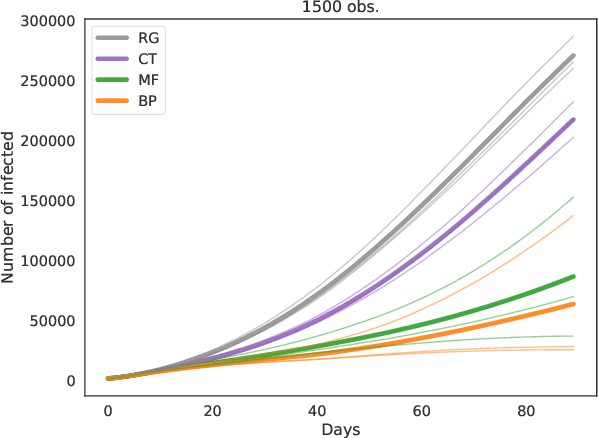
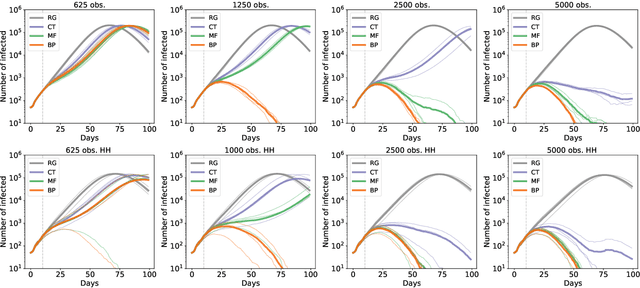
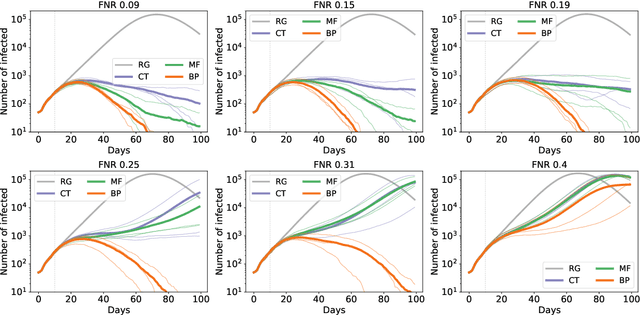
Contact-tracing is an essential tool in order to mitigate the impact of pandemic such as the COVID-19. In order to achieve efficient and scalable contact-tracing in real time, digital devices can play an important role. While a lot of attention has been paid to analyzing the privacy and ethical risks of the associated mobile applications, so far much less research has been devoted to optimizing their performance and assessing their impact on the mitigation of the epidemic. We develop Bayesian inference methods to estimate the risk that an individual is infected. This inference is based on the list of his recent contacts and their own risk levels, as well as personal information such as results of tests or presence of syndromes. We propose to use probabilistic risk estimation in order to optimize testing and quarantining strategies for the control of an epidemic. Our results show that in some range of epidemic spreading (typically when the manual tracing of all contacts of infected people becomes practically impossible, but before the fraction of infected people reaches the scale where a lock-down becomes unavoidable), this inference of individuals at risk could be an efficient way to mitigate the epidemic. Our approaches translate into fully distributed algorithms that only require communication between individuals who have recently been in contact. Such communication may be encrypted and anonymized and thus compatible with privacy preserving standards. We conclude that probabilistic risk estimation is capable to enhance performance of digital contact tracing and should be considered in the currently developed mobile applications.

Compressed sensing reconstruction using Expectation Propagation

Many interesting problems in fields ranging from telecommunications to computational biology can be formalized in terms of large underdetermined systems of linear equations with additional constraints or regularizers. One of the most studied ones, the Compressed Sensing problem (CS), consists in finding the solution with the smallest number of non-zero components of a given system of linear equations $\boldsymbol y = \mathbf{F} \boldsymbol w$ for known measurement vector $\boldsymbol y$ and sensing matrix $\mathbf{F}$. Here, we will address the compressed sensing problem within a Bayesian inference framework where the sparsity constraint is remapped into a singular prior distribution (called Spike-and-Slab or Bernoulli-Gauss). Solution to the problem is attempted through the computation of marginal distributions via Expectation Propagation (EP), an iterative computational scheme originally developed in Statistical Physics. We will show that this strategy is comparatively more accurate than the alternatives in solving instances of CS generated from statistically correlated measurement matrices. For computational strategies based on the Bayesian framework such as variants of Belief Propagation, this is to be expected, as they implicitly rely on the hypothesis of statistical independence among the entries of the sensing matrix. Perhaps surprisingly, the method outperforms uniformly also all the other state-of-the-art methods in our tests.

Loop corrections in spin models through density consistency

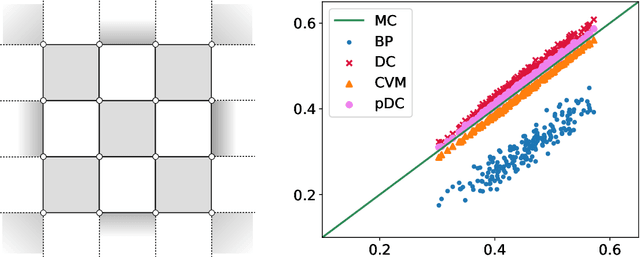
Computing marginal distributions of discrete or semi-discrete Markov Random Fields (MRF) is a fundamental, generally intractable, problem with a vast number of applications on virtually all fields of science. We present a new family of computational schemes to calculate approximately marginals of discrete MRFs. This method shares some desirable properties with Belief Propagation, in particular providing exact marginals on acyclic graphs; but at difference with it, it includes some loop corrections, i.e. it takes into account correlations coming from all cycles in the factor graph. It is also similar to Adaptive TAP, but at difference with it, the consistency is not on the first two moments of the distribution but rather on the value of its density on a subset of values. Results on random connectivity and finite dimensional Ising and Edward-Anderson models show a significant improvement with respect to the Bethe-Peierls (tree) approximation in all cases, and significant improvement with respect to Cluster Variational Method and Loop Corrected Bethe approximation in many cases. In particular, for the critical inverse temperature $\beta_{c}$ of the homogeneous hypercubic lattice, the $1/d$ expansion of $\left(d\beta_{c}\right)^{-1}$ of the proposed scheme is exact up to the $d^{-3}$ order, whereas the two latter are exact only up to the $d^{-2}$ order.

A Max-Sum algorithm for training discrete neural networks

We present an efficient learning algorithm for the problem of training neural networks with discrete synapses, a well-known hard (NP-complete) discrete optimization problem. The algorithm is a variant of the so-called Max-Sum (MS) algorithm. In particular, we show how, for bounded integer weights with $q$ distinct states and independent concave a priori distribution (e.g. $l_{1}$ regularization), the algorithm's time complexity can be made to scale as $O\left(N\log N\right)$ per node update, thus putting it on par with alternative schemes, such as Belief Propagation (BP), without resorting to approximations. Two special cases are of particular interest: binary synapses $W\in\{-1,1\}$ and ternary synapses $W\in\{-1,0,1\}$ with $l_{0}$ regularization. The algorithm we present performs as well as BP on binary perceptron learning problems, and may be better suited to address the problem on fully-connected two-layer networks, since inherent symmetries in two layer networks are naturally broken using the MS approach.

Efficient supervised learning in networks with binary synapses

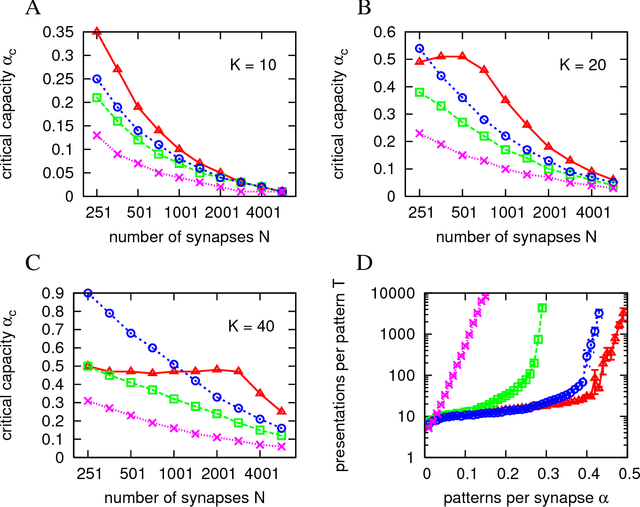
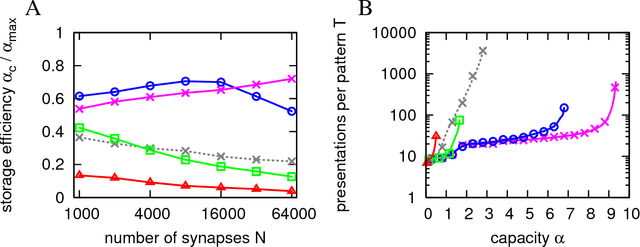
Recent experimental studies indicate that synaptic changes induced by neuronal activity are discrete jumps between a small number of stable states. Learning in systems with discrete synapses is known to be a computationally hard problem. Here, we study a neurobiologically plausible on-line learning algorithm that derives from Belief Propagation algorithms. We show that it performs remarkably well in a model neuron with binary synapses, and a finite number of `hidden' states per synapse, that has to learn a random classification task. Such system is able to learn a number of associations close to the theoretical limit, in time which is sublinear in system size. This is to our knowledge the first on-line algorithm that is able to achieve efficiently a finite number of patterns learned per binary synapse. Furthermore, we show that performance is optimal for a finite number of hidden states which becomes very small for sparse coding. The algorithm is similar to the standard `perceptron' learning algorithm, with an additional rule for synaptic transitions which occur only if a currently presented pattern is `barely correct'. In this case, the synaptic changes are meta-plastic only (change in hidden states and not in actual synaptic state), stabilizing the synapse in its current state. Finally, we show that a system with two visible states and K hidden states is much more robust to noise than a system with K visible states. We suggest this rule is sufficiently simple to be easily implemented by neurobiological systems or in hardware.

Learning by message-passing in networks of discrete synapses

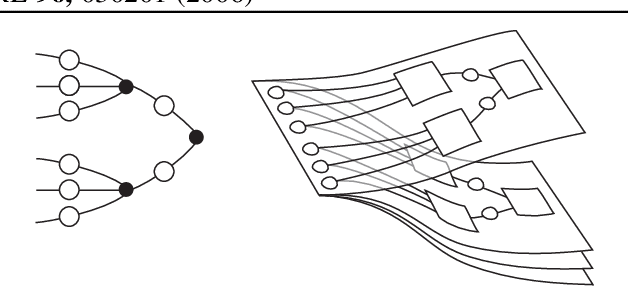
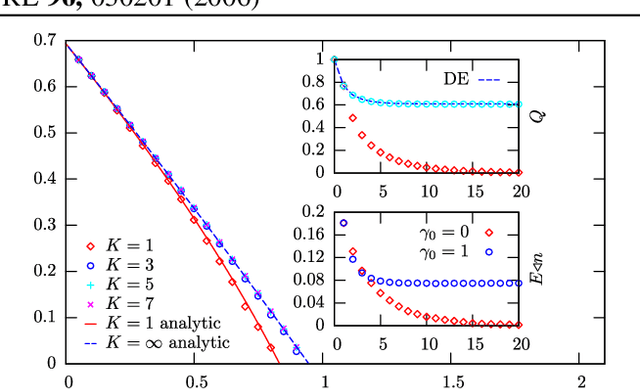
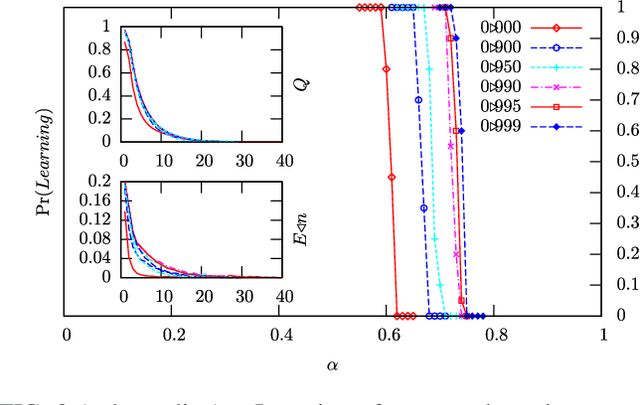
We show that a message-passing process allows to store in binary "material" synapses a number of random patterns which almost saturates the information theoretic bounds. We apply the learning algorithm to networks characterized by a wide range of different connection topologies and of size comparable with that of biological systems (e.g. $n\simeq10^{5}-10^{6}$). The algorithm can be turned into an on-line --fault tolerant-- learning protocol of potential interest in modeling aspects of synaptic plasticity and in building neuromorphic devices.