Supervised and Unsupervised protocols for hetero-associative neural networks

This paper introduces a learning framework for Three-Directional Associative Memory (TAM) models, extending the classical Hebbian paradigm to both supervised and unsupervised protocols within an hetero-associative setting. These neural networks consist of three interconnected layers of binary neurons interacting via generalized Hebbian synaptic couplings that allow learning, storage and retrieval of structured triplets of patterns. By relying upon glassy statistical mechanical techniques (mainly replica theory and Guerra interpolation), we analyze the emergent computational properties of these networks, at work with random (Rademacher) datasets and at the replica-symmetric level of description: we obtain a set of self-consistency equations for the order parameters that quantify the critical dataset sizes (i.e. their thresholds for learning) and describe the retrieval performance of these networks, highlighting the differences between supervised and unsupervised protocols. Numerical simulations validate our theoretical findings and demonstrate the robustness of the captured picture about TAMs also at work with structured datasets. In particular, this study provides insights into the cooperative interplay of layers, beyond that of the neurons within the layers, with potential implications for optimal design of artificial neural network architectures.

Beyond Disorder: Unveiling Cooperativeness in Multidirectional Associative Memories

By leveraging tools from the statistical mechanics of complex systems, in these short notes we extend the architecture of a neural network for hetero-associative memory (called three-directional associative memories, TAM) to explore supervised and unsupervised learning protocols. In particular, by providing entropic-heterogeneous datasets to its various layers, we predict and quantify a new emergent phenomenon -- that we term {\em layer's cooperativeness} -- where the interplay of dataset entropies across network's layers enhances their retrieval capabilities Beyond those they would have without reciprocal influence. Naively we would expect layers trained with less informative datasets to develop smaller retrieval regions compared to those pertaining to layers that experienced more information: this does not happen and all the retrieval regions settle to the same amplitude, allowing for optimal retrieval performance globally. This cooperative dynamics marks a significant advancement in understanding emergent computational capabilities within disordered systems.

Evidence of Replica Symmetry Breaking under the Nishimori conditions in epidemic inference on graphs

In Bayesian inference, computing the posterior distribution from the data is typically a non-trivial problem, which usually requires approximations such as mean-field approaches or numerical methods, like the Monte Carlo Markov Chain. Being a high-dimensional distribution over a set of correlated variables, the posterior distribution can undergo the notorious replica symmetry breaking transition. When it happens, several mean-field methods and virtually every Monte Carlo scheme can not provide a reasonable approximation to the posterior and its marginals. Replica symmetry is believed to be guaranteed whenever the data is generated with known prior and likelihood distributions, namely under the so-called Nishimori conditions. In this paper, we break this belief, by providing a counter-example showing that, under the Nishimori conditions, replica symmetry breaking arises. Introducing a simple, geometrical model that can be thought of as a patient zero retrieval problem in a highly infectious regime of the epidemic Susceptible-Infectious model, we show that under the Nishimori conditions, there is evidence of replica symmetry breaking. We achieve this result by computing the instability of the replica symmetric cavity method toward the one step replica symmetry broken phase. The origin of this phenomenon -- replica symmetry breaking under the Nishimori conditions -- is likely due to the correlated disorder appearing in the epidemic models.

Stochastic Gradient Descent-like relaxation is equivalent to Glauber dynamics in discrete optimization and inference problems

Is Stochastic Gradient Descent (SGD) substantially different from Glauber dynamics? This is a fundamental question at the time of understanding the most used training algorithm in the field of Machine Learning, but it received no answer until now. Here we show that in discrete optimization and inference problems, the dynamics of an SGD-like algorithm resemble very closely that of Metropolis Monte Carlo with a properly chosen temperature, which depends on the mini-batch size. This quantitative matching holds both at equilibrium and in the out-of-equilibrium regime, despite the two algorithms having fundamental differences (e.g.\ SGD does not satisfy detailed balance). Such equivalence allows us to use results about performances and limits of Monte Carlo algorithms to optimize the mini-batch size in the SGD-like algorithm and make it efficient at recovering the signal in hard inference problems.

Parallel Learning by Multitasking Neural Networks

A modern challenge of Artificial Intelligence is learning multiple patterns at once (i.e.parallel learning). While this can not be accomplished by standard Hebbian associative neural networks, in this paper we show how the Multitasking Hebbian Network (a variation on theme of the Hopfield model working on sparse data-sets) is naturally able to perform this complex task. We focus on systems processing in parallel a finite (up to logarithmic growth in the size of the network) amount of patterns, mirroring the low-storage level of standard associative neural networks at work with pattern recognition. For mild dilution in the patterns, the network handles them hierarchically, distributing the amplitudes of their signals as power-laws w.r.t. their information content (hierarchical regime), while, for strong dilution, all the signals pertaining to all the patterns are raised with the same strength (parallel regime). Further, confined to the low-storage setting (i.e., far from the spin glass limit), the presence of a teacher neither alters the multitasking performances nor changes the thresholds for learning: the latter are the same whatever the training protocol is supervised or unsupervised. Results obtained through statistical mechanics, signal-to-noise technique and Monte Carlo simulations are overall in perfect agreement and carry interesting insights on multiple learning at once: for instance, whenever the cost-function of the model is minimized in parallel on several patterns (in its description via Statistical Mechanics), the same happens to the standard sum-squared error Loss function (typically used in Machine Learning).

Phase transitions in the mini-batch size for sparse and dense neural networks

The use of mini-batches of data in training artificial neural networks is nowadays very common. Despite its broad usage, theories explaining quantitatively how large or small the optimal mini-batch size should be are missing. This work presents a systematic attempt at understanding the role of the mini-batch size in training two-layer neural networks. Working in the teacher-student scenario, with a sparse teacher, and focusing on tasks of different complexity, we quantify the effects of changing the mini-batch size $m$. We find that often the generalization performances of the student strongly depend on $m$ and may undergo sharp phase transitions at a critical value $m_c$, such that for $m<m_c$ the training process fails, while for $m>m_c$ the student learns perfectly or generalizes very well the teacher. Phase transitions are induced by collective phenomena firstly discovered in statistical mechanics and later observed in many fields of science. Finding a phase transition varying the mini-batch size raises several important questions on the role of a hyperparameter which have been somehow overlooked until now.

Multi-mode fiber reservoir computing overcomes shallow neural networks classifiers

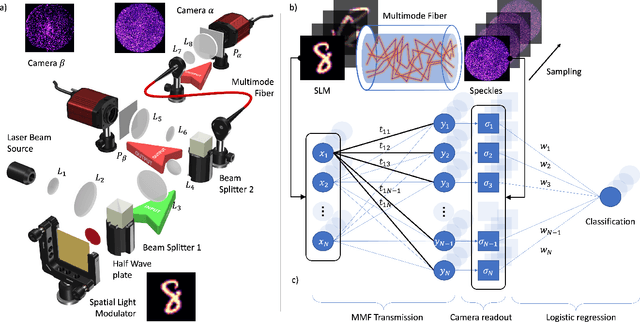
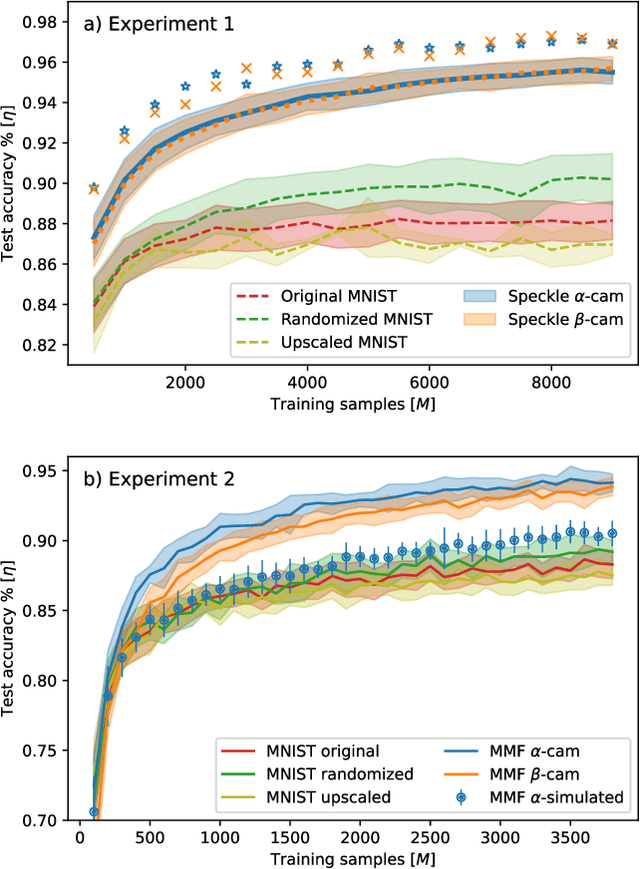
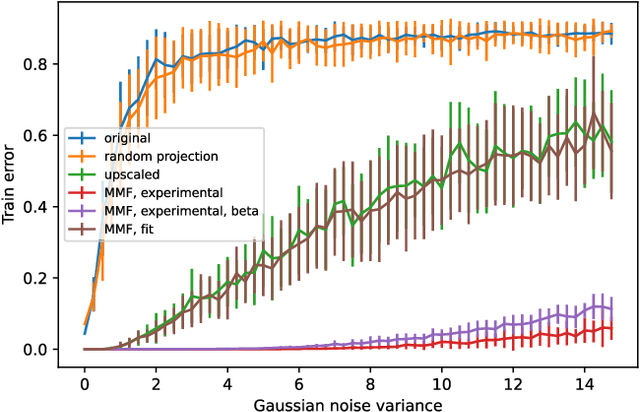
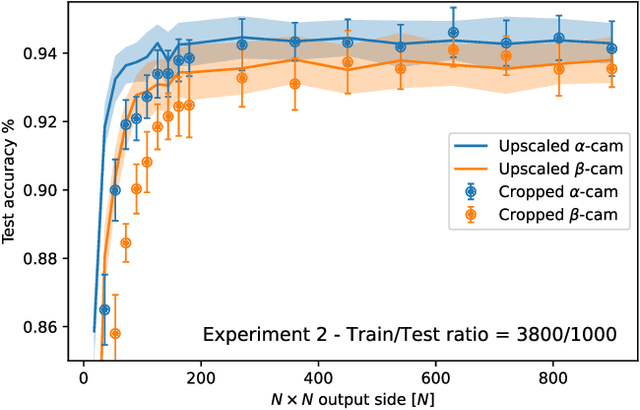
In disordered photonics, one typically tries to characterize the optically opaque material in order to be able to deliver light or perform imaging through it. Among others, multi-mode optical fibers are extensively studied because they are cheap and easy-to-handle complex devices. Here, instead, we use the reservoir computing paradigm to turn these optical tools into random projectors capable of introducing a sufficient amount of interaction to perform non-linear classification. We show that training a single logistic regression layer on the data projected by the fiber improves the accuracy with respect to learning it on the raw images. Surprisingly, the classification accuracy performed with physical measurements is higher than the one obtained using the standard transmission matrix model, a widely accepted tool to describe light transmission through disordered devices. Consistently with the current theory of deep neural networks, we also reveal that the classifier lives in a flatter region of the loss landscape when trained on fiber data. These facts suggest that multi-mode fibers exhibit robust generalization properties, thus making them promising tools for optically-aided machine learning.

Cracking nuts with a sledgehammer: when modern graph neural networks do worse than classical greedy algorithms

The recent work ``Combinatorial Optimization with Physics-Inspired Graph Neural Networks'' [Nat Mach Intell 4 (2022) 367] introduces a physics-inspired unsupervised Graph Neural Network (GNN) to solve combinatorial optimization problems on sparse graphs. To test the performances of these GNNs, the authors of the work show numerical results for two fundamental problems: maximum cut and maximum independent set (MIS). They conclude that "the graph neural network optimizer performs on par or outperforms existing solvers, with the ability to scale beyond the state of the art to problems with millions of variables." In this comment, we show that a simple greedy algorithm, running in almost linear time, can find solutions for the MIS problem of much better quality than the GNN. The greedy algorithm is faster by a factor of $10^4$ with respect to the GNN for problems with a million variables. We do not see any good reason for solving the MIS with these GNN, as well as for using a sledgehammer to crack nuts. In general, many claims of superiority of neural networks in solving combinatorial problems are at risk of being not solid enough, since we lack standard benchmarks based on really hard problems. We propose one of such hard benchmarks, and we hope to see future neural network optimizers tested on these problems before any claim of superiority is made.

Nonequilibrium Monte Carlo for unfreezing variables in hard combinatorial optimization

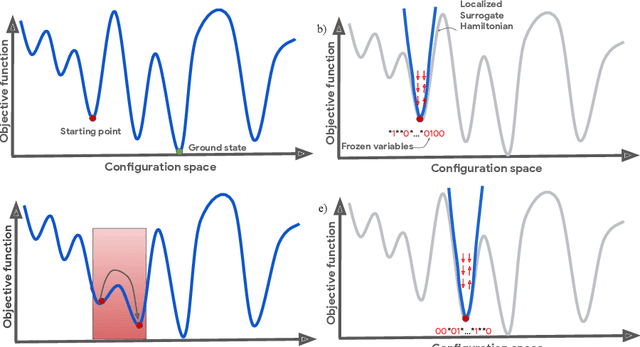
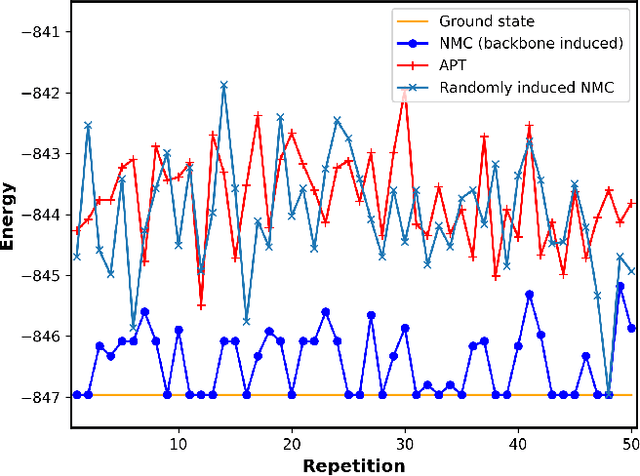
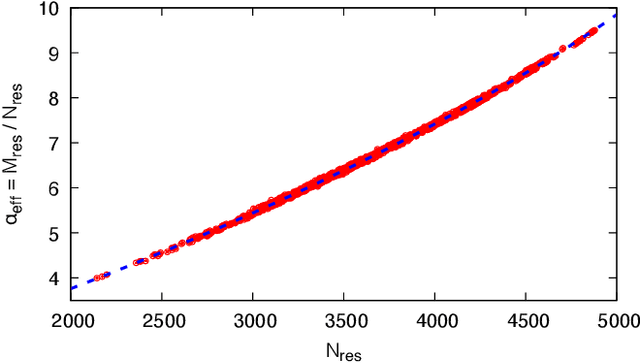
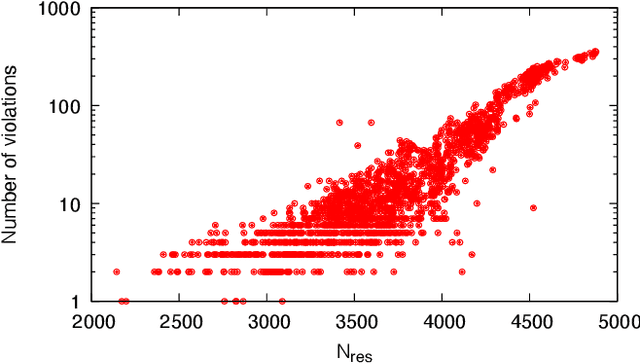
Optimizing highly complex cost/energy functions over discrete variables is at the heart of many open problems across different scientific disciplines and industries. A major obstacle is the emergence of many-body effects among certain subsets of variables in hard instances leading to critical slowing down or collective freezing for known stochastic local search strategies. An exponential computational effort is generally required to unfreeze such variables and explore other unseen regions of the configuration space. Here, we introduce a quantum-inspired family of nonlocal Nonequilibrium Monte Carlo (NMC) algorithms by developing an adaptive gradient-free strategy that can efficiently learn key instance-wise geometrical features of the cost function. That information is employed on-the-fly to construct spatially inhomogeneous thermal fluctuations for collectively unfreezing variables at various length scales, circumventing costly exploration versus exploitation trade-offs. We apply our algorithm to two of the most challenging combinatorial optimization problems: random k-satisfiability (k-SAT) near the computational phase transitions and Quadratic Assignment Problems (QAP). We observe significant speedup and robustness over both specialized deterministic solvers and generic stochastic solvers. In particular, for 90% of random 4-SAT instances we find solutions that are inaccessible for the best specialized deterministic algorithm known as Survey Propagation (SP) with an order of magnitude improvement in the quality of solutions for the hardest 10% instances. We also demonstrate two orders of magnitude improvement in time-to-solution over the state-of-the-art generic stochastic solver known as Adaptive Parallel Tempering (APT).

How to iron out rough landscapes and get optimal performances: Replicated Gradient Descent and its application to tensor PCA

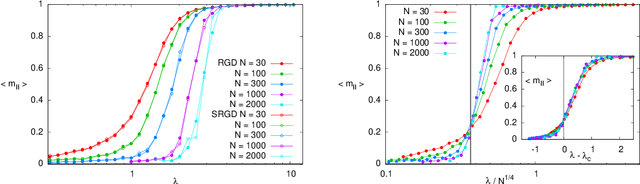
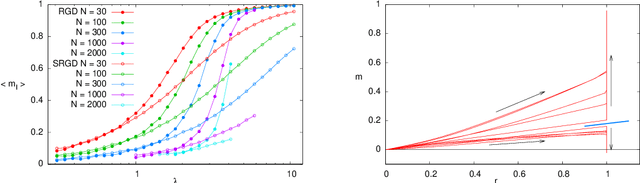
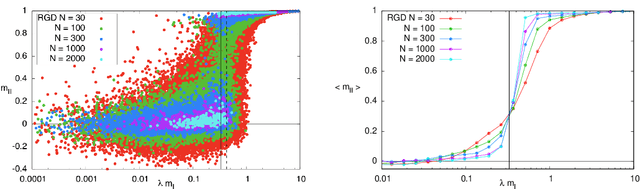
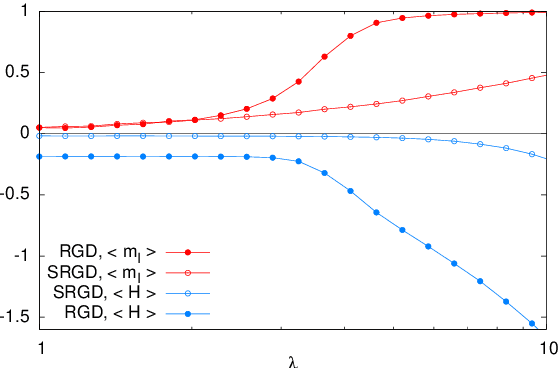
In many high-dimensional estimation problems the main task consists in minimizing a cost function, which is often strongly non-convex when scanned in the space of parameters to be estimated. A standard solution to flatten the corresponding rough landscape consists in summing the losses associated to different data points and obtain a smoother empirical risk. Here we propose a complementary method that works for a single data point. The main idea is that a large amount of the roughness is uncorrelated in different parts of the landscape. One can then substantially reduce the noise by evaluating an empirical average of the gradient obtained as a sum over many random independent positions in the space of parameters to be optimized. We present an algorithm, called Replicated Gradient Descent, based on this idea and we apply it to tensor PCA, which is a very hard estimation problem. We show that Replicated Gradient Descent over-performs physical algorithms such as gradient descent and approximate message passing and matches the best algorithmic thresholds known so far, obtained by tensor unfolding and methods based on sum-of-squares.