Nonequilibrium Monte Carlo for unfreezing variables in hard combinatorial optimization

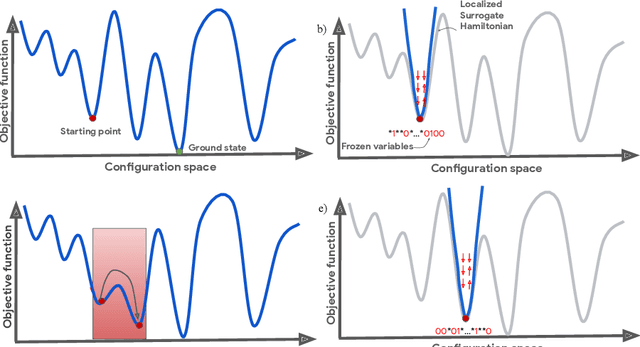
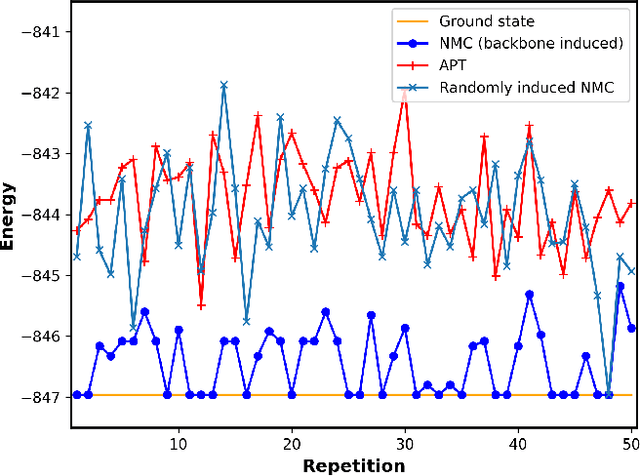
Optimizing highly complex cost/energy functions over discrete variables is at the heart of many open problems across different scientific disciplines and industries. A major obstacle is the emergence of many-body effects among certain subsets of variables in hard instances leading to critical slowing down or collective freezing for known stochastic local search strategies. An exponential computational effort is generally required to unfreeze such variables and explore other unseen regions of the configuration space. Here, we introduce a quantum-inspired family of nonlocal Nonequilibrium Monte Carlo (NMC) algorithms by developing an adaptive gradient-free strategy that can efficiently learn key instance-wise geometrical features of the cost function. That information is employed on-the-fly to construct spatially inhomogeneous thermal fluctuations for collectively unfreezing variables at various length scales, circumventing costly exploration versus exploitation trade-offs. We apply our algorithm to two of the most challenging combinatorial optimization problems: random k-satisfiability (k-SAT) near the computational phase transitions and Quadratic Assignment Problems (QAP). We observe significant speedup and robustness over both specialized deterministic solvers and generic stochastic solvers. In particular, for 90% of random 4-SAT instances we find solutions that are inaccessible for the best specialized deterministic algorithm known as Survey Propagation (SP) with an order of magnitude improvement in the quality of solutions for the hardest 10% instances. We also demonstrate two orders of magnitude improvement in time-to-solution over the state-of-the-art generic stochastic solver known as Adaptive Parallel Tempering (APT).

Construction of non-convex polynomial loss functions for training a binary classifier with quantum annealing

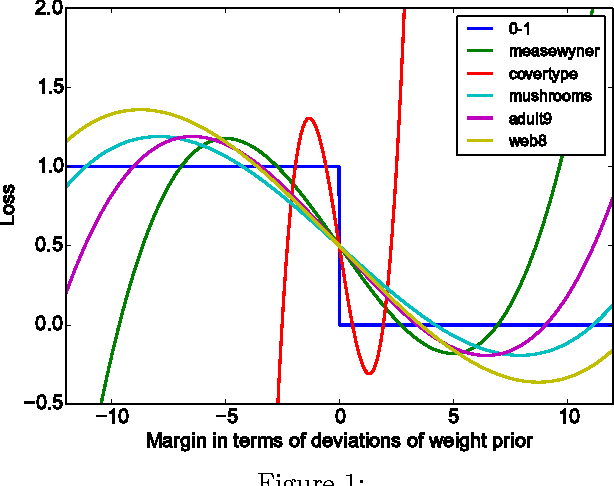
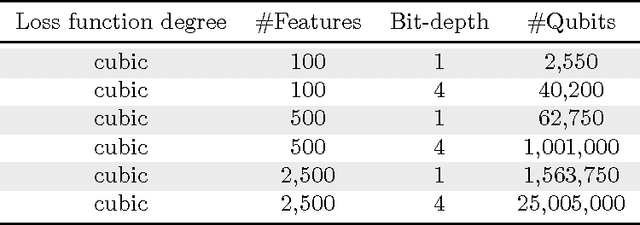
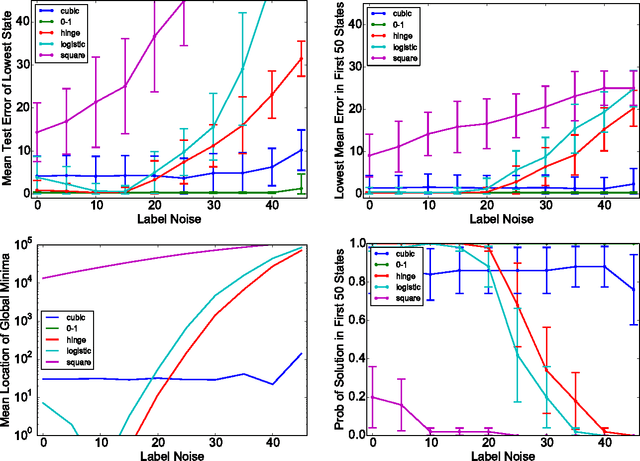
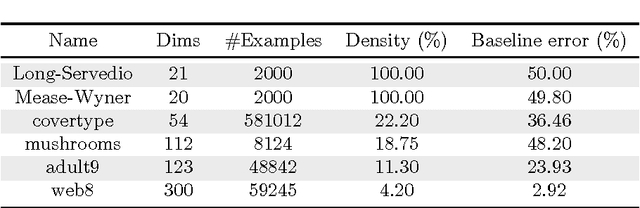
Quantum annealing is a heuristic quantum algorithm which exploits quantum resources to minimize an objective function embedded as the energy levels of a programmable physical system. To take advantage of a potential quantum advantage, one needs to be able to map the problem of interest to the native hardware with reasonably low overhead. Because experimental considerations constrain our objective function to take the form of a low degree PUBO (polynomial unconstrained binary optimization), we employ non-convex loss functions which are polynomial functions of the margin. We show that these loss functions are robust to label noise and provide a clear advantage over convex methods. These loss functions may also be useful for classical approaches as they compile to regularized risk expressions which can be evaluated in constant time with respect to the number of training examples.