Nonequilibrium Monte Carlo for unfreezing variables in hard combinatorial optimization

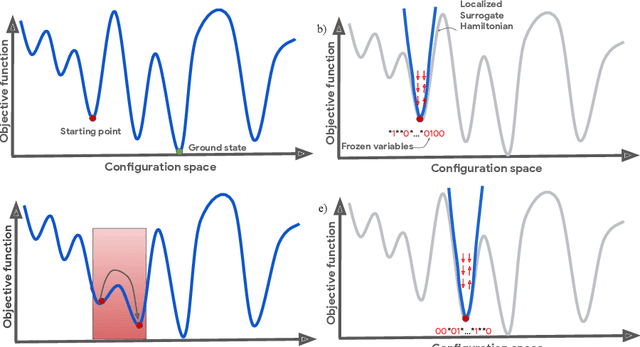
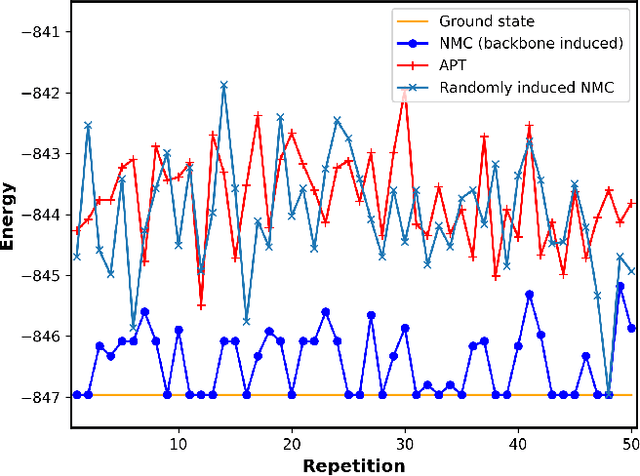
Optimizing highly complex cost/energy functions over discrete variables is at the heart of many open problems across different scientific disciplines and industries. A major obstacle is the emergence of many-body effects among certain subsets of variables in hard instances leading to critical slowing down or collective freezing for known stochastic local search strategies. An exponential computational effort is generally required to unfreeze such variables and explore other unseen regions of the configuration space. Here, we introduce a quantum-inspired family of nonlocal Nonequilibrium Monte Carlo (NMC) algorithms by developing an adaptive gradient-free strategy that can efficiently learn key instance-wise geometrical features of the cost function. That information is employed on-the-fly to construct spatially inhomogeneous thermal fluctuations for collectively unfreezing variables at various length scales, circumventing costly exploration versus exploitation trade-offs. We apply our algorithm to two of the most challenging combinatorial optimization problems: random k-satisfiability (k-SAT) near the computational phase transitions and Quadratic Assignment Problems (QAP). We observe significant speedup and robustness over both specialized deterministic solvers and generic stochastic solvers. In particular, for 90% of random 4-SAT instances we find solutions that are inaccessible for the best specialized deterministic algorithm known as Survey Propagation (SP) with an order of magnitude improvement in the quality of solutions for the hardest 10% instances. We also demonstrate two orders of magnitude improvement in time-to-solution over the state-of-the-art generic stochastic solver known as Adaptive Parallel Tempering (APT).

TensorFlow Quantum: A Software Framework for Quantum Machine Learning

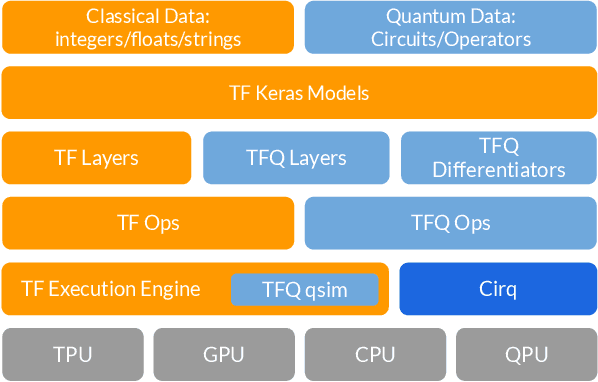
We introduce TensorFlow Quantum (TFQ), an open source library for the rapid prototyping of hybrid quantum-classical models for classical or quantum data. This framework offers high-level abstractions for the design and training of both discriminative and generative quantum models under TensorFlow and supports high-performance quantum circuit simulators. We provide an overview of the software architecture and building blocks through several examples and review the theory of hybrid quantum-classical neural networks. We illustrate TFQ functionalities via several basic applications including supervised learning for quantum classification, quantum control, and quantum approximate optimization. Moreover, we demonstrate how one can apply TFQ to tackle advanced quantum learning tasks including meta-learning, Hamiltonian learning, and sampling thermal states. We hope this framework provides the necessary tools for the quantum computing and machine learning research communities to explore models of both natural and artificial quantum systems, and ultimately discover new quantum algorithms which could potentially yield a quantum advantage.

Quantum-Assisted Genetic Algorithm

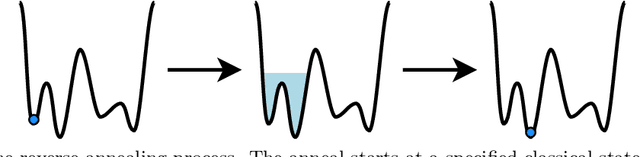
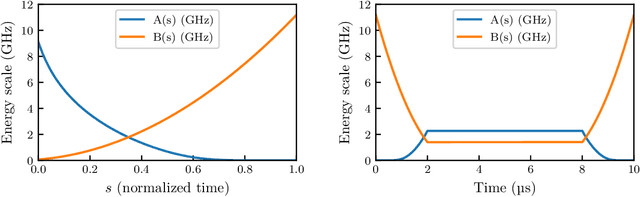
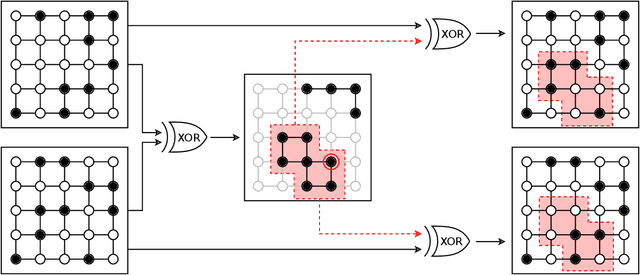
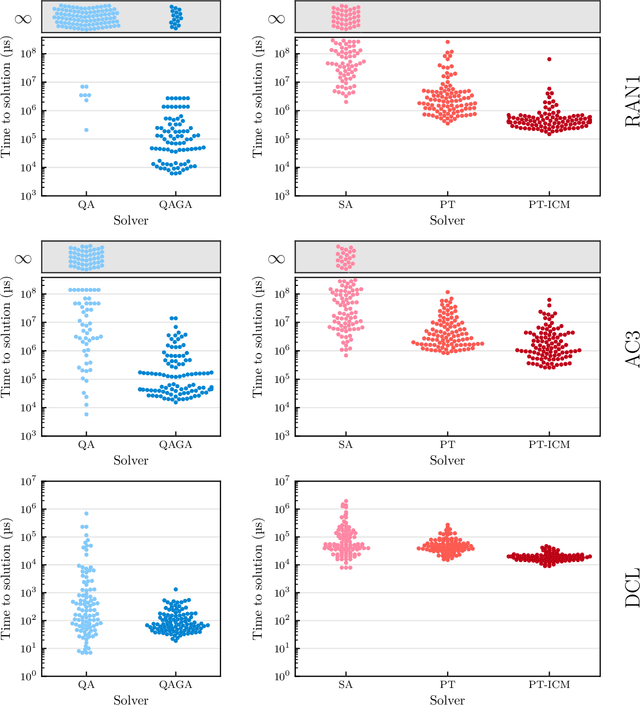
Genetic algorithms, which mimic evolutionary processes to solve optimization problems, can be enhanced by using powerful semi-local search algorithms as mutation operators. Here, we introduce reverse quantum annealing, a class of quantum evolutions that can be used for performing families of quasi-local or quasi-nonlocal search starting from a classical state, as novel sources of mutations. Reverse annealing enables the development of genetic algorithms that use quantum fluctuation for mutations and classical mechanisms for the crossovers -- we refer to these as Quantum-Assisted Genetic Algorithms (QAGAs). We describe a QAGA and present experimental results using a D-Wave 2000Q quantum annealing processor. On a set of spin-glass inputs, standard (forward) quantum annealing finds good solutions very quickly but struggles to find global optima. In contrast, our QAGA proves effective at finding global optima for these inputs. This successful interplay of non-local classical and quantum fluctuations could provide a promising step toward practical applications of Noisy Intermediate-Scale Quantum (NISQ) devices for heuristic discrete optimization.