A Path Towards Quantum Advantage in Training Deep Generative Models with Quantum Annealers

The development of quantum-classical hybrid (QCH) algorithms is critical to achieve state-of-the-art computational models. A QCH variational autoencoder (QVAE) was introduced in Ref. [1] by some of the authors of this paper. QVAE consists of a classical auto-encoding structure realized by traditional deep neural networks to perform inference to, and generation from, a discrete latent space. The latent generative process is formalized as thermal sampling from either a quantum or classical Boltzmann machine (QBM or BM). This setup allows quantum-assisted training of deep generative models by physically simulating the generative process with quantum annealers. In this paper, we have successfully employed D-Wave quantum annealers as Boltzmann samplers to perform quantum-assisted, end-to-end training of QVAE. The hybrid structure of QVAE allows us to deploy current-generation quantum annealers in QCH generative models to achieve competitive performance on datasets such as MNIST. The results presented in this paper suggest that commercially available quantum annealers can be deployed, in conjunction with well-crafted classical deep neutral networks, to achieve competitive results in unsupervised and semisupervised tasks on large-scale datasets. We also provide evidence that our setup is able to exploit large latent-space (Q)BMs, which develop slowly mixing modes. This expressive latent space results in slow and inefficient classical sampling, and paves the way to achieve quantum advantage with quantum annealing in realistic sampling applications.

PixelVAE++: Improved PixelVAE with Discrete Prior

Constructing powerful generative models for natural images is a challenging task. PixelCNN models capture details and local information in images very well but have limited receptive field. Variational autoencoders with a factorial decoder can capture global information easily, but they often fail to reconstruct details faithfully. PixelVAE combines the best features of the two models and constructs a generative model that is able to learn local and global structures. Here we introduce PixelVAE++, a VAE with three types of latent variables and a PixelCNN++ for the decoder. We introduce a novel architecture that reuses a part of the decoder as an encoder. We achieve the state of the art performance on binary data sets such as MNIST and Omniglot and achieve the state of the art performance on CIFAR-10 among latent variable models while keeping the latent variables informative.

Quantum-Assisted Genetic Algorithm

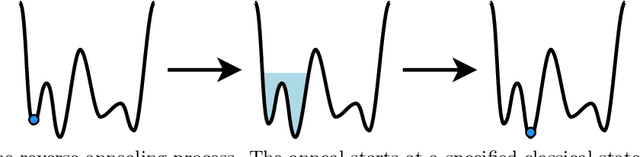
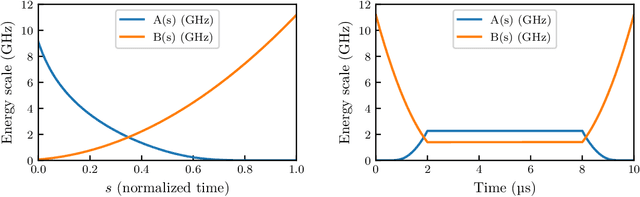
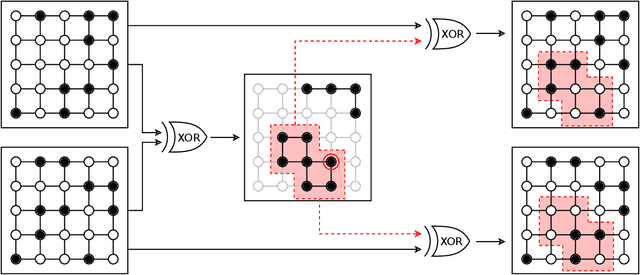
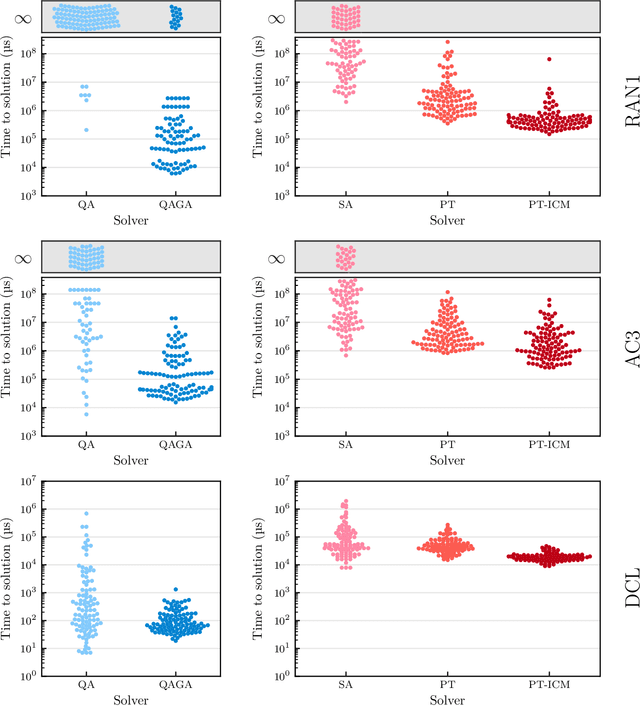
Genetic algorithms, which mimic evolutionary processes to solve optimization problems, can be enhanced by using powerful semi-local search algorithms as mutation operators. Here, we introduce reverse quantum annealing, a class of quantum evolutions that can be used for performing families of quasi-local or quasi-nonlocal search starting from a classical state, as novel sources of mutations. Reverse annealing enables the development of genetic algorithms that use quantum fluctuation for mutations and classical mechanisms for the crossovers -- we refer to these as Quantum-Assisted Genetic Algorithms (QAGAs). We describe a QAGA and present experimental results using a D-Wave 2000Q quantum annealing processor. On a set of spin-glass inputs, standard (forward) quantum annealing finds good solutions very quickly but struggles to find global optima. In contrast, our QAGA proves effective at finding global optima for these inputs. This successful interplay of non-local classical and quantum fluctuations could provide a promising step toward practical applications of Noisy Intermediate-Scale Quantum (NISQ) devices for heuristic discrete optimization.

GumBolt: Extending Gumbel trick to Boltzmann priors

Boltzmann machines (BMs) are appealing candidates for powerful priors in variational autoencoders (VAEs), as they are capable of capturing nontrivial and multi-modal distributions over discrete variables. However, indifferentiability of the discrete units prohibits using the reparameterization trick, essential for low-noise back propagation. The Gumbel trick resolves this problem in a consistent way by relaxing the variables and distributions, but it is incompatible with BM priors. Here, we propose the GumBolt, a model that extends the Gumbel trick to BM priors in VAEs. GumBolt is significantly simpler than the recently proposed methods with BM prior and outperforms them by a considerable margin. It achieves state-of-the-art performance on permutation invariant MNIST and OMNIGLOT datasets in the scope of models with only discrete latent variables. Moreover, the performance can be further improved by allowing multi-sampled (importance-weighted) estimation of log-likelihood in training, which was not possible with previous models.

Quantum Variational Autoencoder

Variational autoencoders (VAEs) are powerful generative models with the salient ability to perform inference. Here, we introduce a \emph{quantum variational autoencoder} (QVAE): a VAE whose latent generative process is implemented as a quantum Boltzmann machine (QBM). We show that our model can be trained end-to-end by maximizing a well-defined loss-function: a "quantum" lower-bound to a variational approximation of the log-likelihood. We use quantum Monte Carlo (QMC) simulations to train and evaluate the performance of QVAEs. To achieve the best performance, we first create a VAE platform with discrete latent space generated by a restricted Boltzmann machine (RBM). Our model achieves state-of-the-art performance on the MNIST dataset when compared against similar approaches that only involve discrete variables in the generative process. We consider QVAEs with a smaller number of latent units to be able to perform QMC simulations, which are computationally expensive. We show that QVAEs can be trained effectively in regimes where quantum effects are relevant despite training via the quantum bound. Our findings open the way to the use of quantum computers to train QVAEs to achieve competitive performance for generative models. Placing a QBM in the latent space of a VAE leverages the full potential of current and next-generation quantum computers as sampling devices.