Quantum-Assisted Genetic Algorithm
Paper and Code
Jun 24, 2019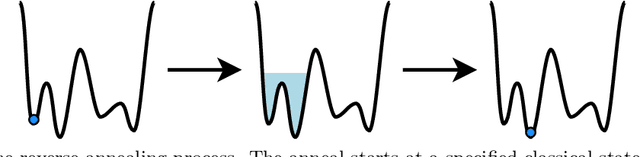
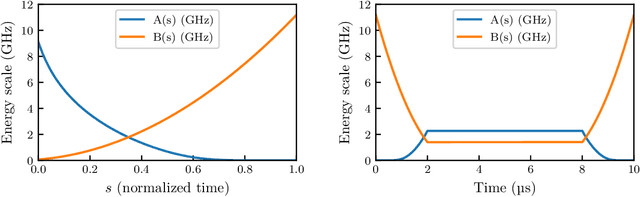
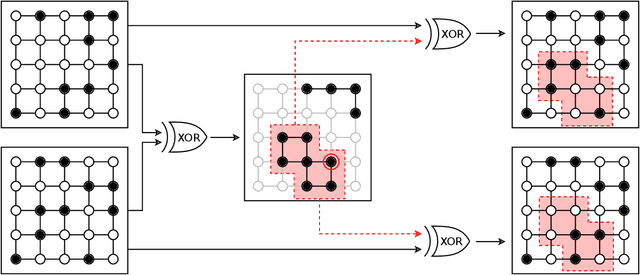
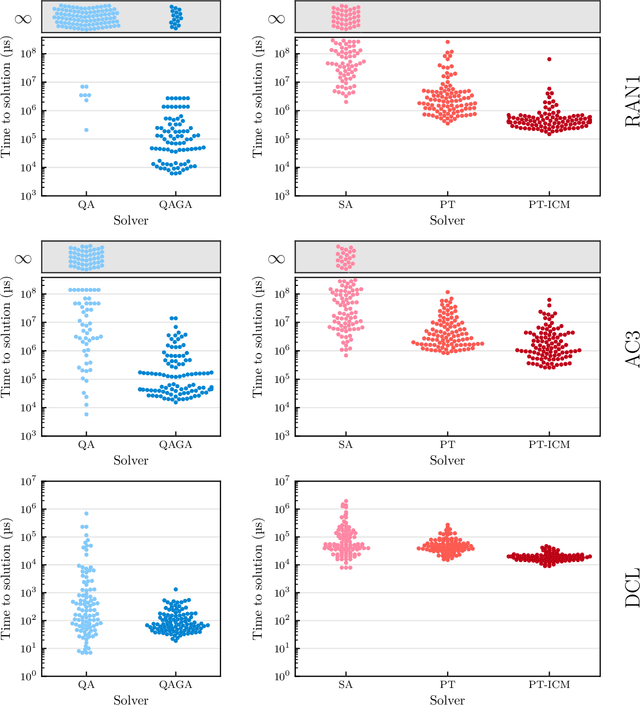
Genetic algorithms, which mimic evolutionary processes to solve optimization problems, can be enhanced by using powerful semi-local search algorithms as mutation operators. Here, we introduce reverse quantum annealing, a class of quantum evolutions that can be used for performing families of quasi-local or quasi-nonlocal search starting from a classical state, as novel sources of mutations. Reverse annealing enables the development of genetic algorithms that use quantum fluctuation for mutations and classical mechanisms for the crossovers -- we refer to these as Quantum-Assisted Genetic Algorithms (QAGAs). We describe a QAGA and present experimental results using a D-Wave 2000Q quantum annealing processor. On a set of spin-glass inputs, standard (forward) quantum annealing finds good solutions very quickly but struggles to find global optima. In contrast, our QAGA proves effective at finding global optima for these inputs. This successful interplay of non-local classical and quantum fluctuations could provide a promising step toward practical applications of Noisy Intermediate-Scale Quantum (NISQ) devices for heuristic discrete optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge