Amir Khoshaman
Nonlocal optimization of binary neural networks
Apr 05, 2022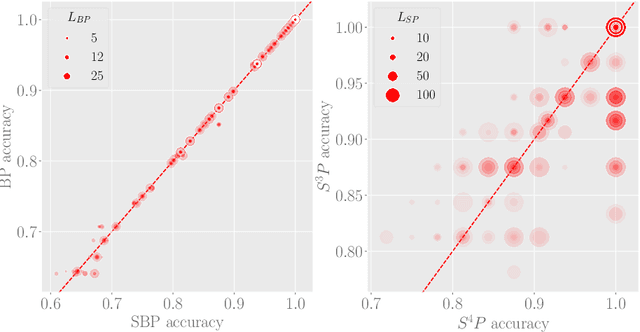
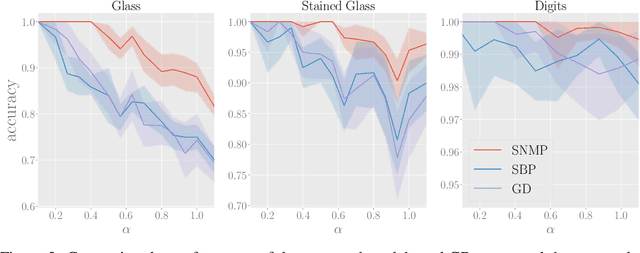
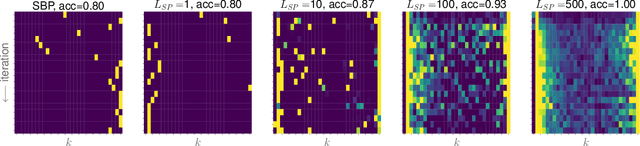
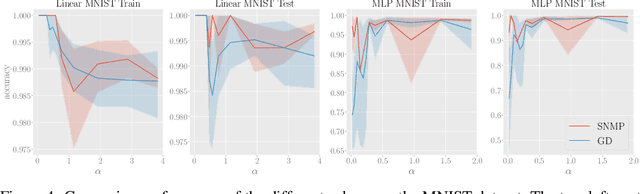
Abstract:We explore training Binary Neural Networks (BNNs) as a discrete variable inference problem over a factor graph. We study the behaviour of this conversion in an under-parameterized BNN setting and propose stochastic versions of Belief Propagation (BP) and Survey Propagation (SP) message passing algorithms to overcome the intractability of their current formulation. Compared to traditional gradient methods for BNNs, our results indicate that both stochastic BP and SP find better configurations of the parameters in the BNN.
A Path Towards Quantum Advantage in Training Deep Generative Models with Quantum Annealers
Dec 04, 2019



Abstract:The development of quantum-classical hybrid (QCH) algorithms is critical to achieve state-of-the-art computational models. A QCH variational autoencoder (QVAE) was introduced in Ref. [1] by some of the authors of this paper. QVAE consists of a classical auto-encoding structure realized by traditional deep neural networks to perform inference to, and generation from, a discrete latent space. The latent generative process is formalized as thermal sampling from either a quantum or classical Boltzmann machine (QBM or BM). This setup allows quantum-assisted training of deep generative models by physically simulating the generative process with quantum annealers. In this paper, we have successfully employed D-Wave quantum annealers as Boltzmann samplers to perform quantum-assisted, end-to-end training of QVAE. The hybrid structure of QVAE allows us to deploy current-generation quantum annealers in QCH generative models to achieve competitive performance on datasets such as MNIST. The results presented in this paper suggest that commercially available quantum annealers can be deployed, in conjunction with well-crafted classical deep neutral networks, to achieve competitive results in unsupervised and semisupervised tasks on large-scale datasets. We also provide evidence that our setup is able to exploit large latent-space (Q)BMs, which develop slowly mixing modes. This expressive latent space results in slow and inefficient classical sampling, and paves the way to achieve quantum advantage with quantum annealing in realistic sampling applications.
DVAE++: Discrete Variational Autoencoders with Overlapping Transformations
May 25, 2018



Abstract:Training of discrete latent variable models remains challenging because passing gradient information through discrete units is difficult. We propose a new class of smoothing transformations based on a mixture of two overlapping distributions, and show that the proposed transformation can be used for training binary latent models with either directed or undirected priors. We derive a new variational bound to efficiently train with Boltzmann machine priors. Using this bound, we develop DVAE++, a generative model with a global discrete prior and a hierarchy of convolutional continuous variables. Experiments on several benchmarks show that overlapping transformations outperform other recent continuous relaxations of discrete latent variables including Gumbel-Softmax (Maddison et al., 2016; Jang et al., 2016), and discrete variational autoencoders (Rolfe 2016).
Quantum Variational Autoencoder
Feb 15, 2018


Abstract:Variational autoencoders (VAEs) are powerful generative models with the salient ability to perform inference. Here, we introduce a \emph{quantum variational autoencoder} (QVAE): a VAE whose latent generative process is implemented as a quantum Boltzmann machine (QBM). We show that our model can be trained end-to-end by maximizing a well-defined loss-function: a "quantum" lower-bound to a variational approximation of the log-likelihood. We use quantum Monte Carlo (QMC) simulations to train and evaluate the performance of QVAEs. To achieve the best performance, we first create a VAE platform with discrete latent space generated by a restricted Boltzmann machine (RBM). Our model achieves state-of-the-art performance on the MNIST dataset when compared against similar approaches that only involve discrete variables in the generative process. We consider QVAEs with a smaller number of latent units to be able to perform QMC simulations, which are computationally expensive. We show that QVAEs can be trained effectively in regimes where quantum effects are relevant despite training via the quantum bound. Our findings open the way to the use of quantum computers to train QVAEs to achieve competitive performance for generative models. Placing a QBM in the latent space of a VAE leverages the full potential of current and next-generation quantum computers as sampling devices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge