DVAE++: Discrete Variational Autoencoders with Overlapping Transformations

Training of discrete latent variable models remains challenging because passing gradient information through discrete units is difficult. We propose a new class of smoothing transformations based on a mixture of two overlapping distributions, and show that the proposed transformation can be used for training binary latent models with either directed or undirected priors. We derive a new variational bound to efficiently train with Boltzmann machine priors. Using this bound, we develop DVAE++, a generative model with a global discrete prior and a hierarchy of convolutional continuous variables. Experiments on several benchmarks show that overlapping transformations outperform other recent continuous relaxations of discrete latent variables including Gumbel-Softmax (Maddison et al., 2016; Jang et al., 2016), and discrete variational autoencoders (Rolfe 2016).

Benchmarking Quantum Hardware for Training of Fully Visible Boltzmann Machines

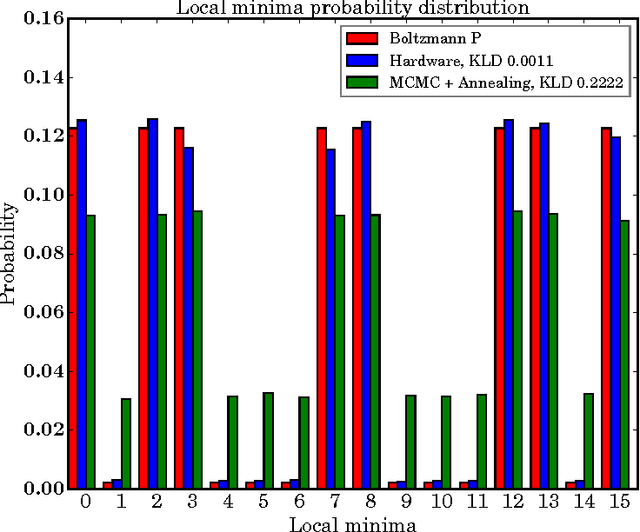
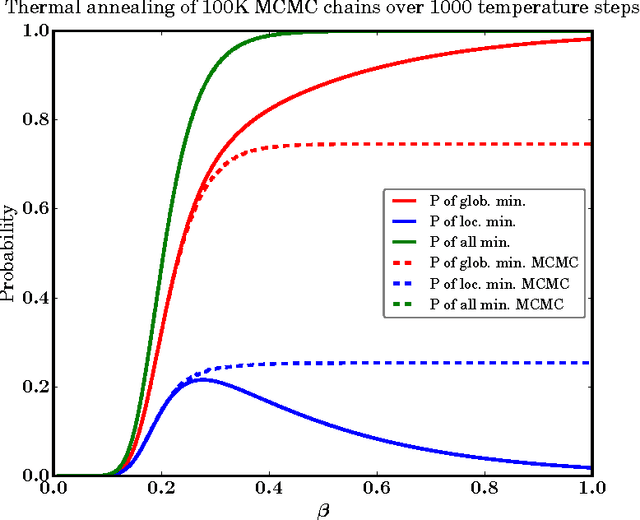
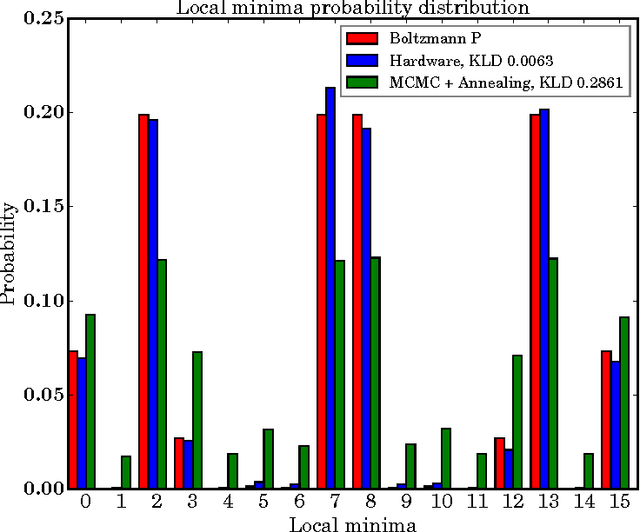
Quantum annealing (QA) is a hardware-based heuristic optimization and sampling method applicable to discrete undirected graphical models. While similar to simulated annealing, QA relies on quantum, rather than thermal, effects to explore complex search spaces. For many classes of problems, QA is known to offer computational advantages over simulated annealing. Here we report on the ability of recent QA hardware to accelerate training of fully visible Boltzmann machines. We characterize the sampling distribution of QA hardware, and show that in many cases, the quantum distributions differ significantly from classical Boltzmann distributions. In spite of this difference, training (which seeks to match data and model statistics) using standard classical gradient updates is still effective. We investigate the use of QA for seeding Markov chains as an alternative to contrastive divergence (CD) and persistent contrastive divergence (PCD). Using $k=50$ Gibbs steps, we show that for problems with high-energy barriers between modes, QA-based seeds can improve upon chains with CD and PCD initializations. For these hard problems, QA gradient estimates are more accurate, and allow for faster learning. Furthermore, and interestingly, even the case of raw QA samples (that is, $k=0$) achieved similar improvements. We argue that this relates to the fact that we are training a quantum rather than classical Boltzmann distribution in this case. The learned parameters give rise to hardware QA distributions closely approximating classical Boltzmann distributions that are hard to train with CD/PCD.