Benchmarking Quantum Hardware for Training of Fully Visible Boltzmann Machines

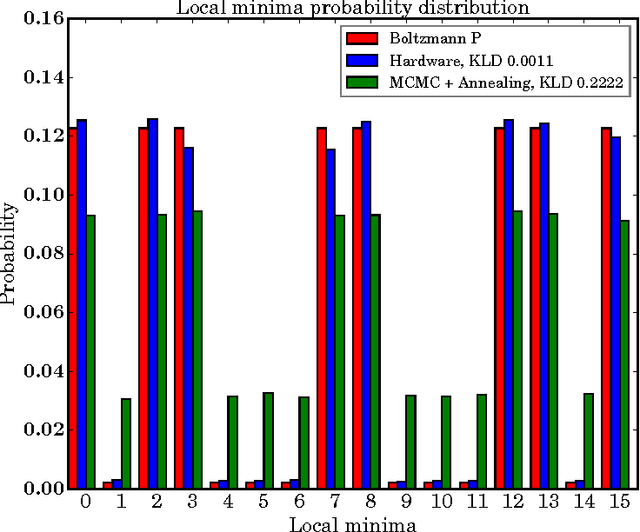
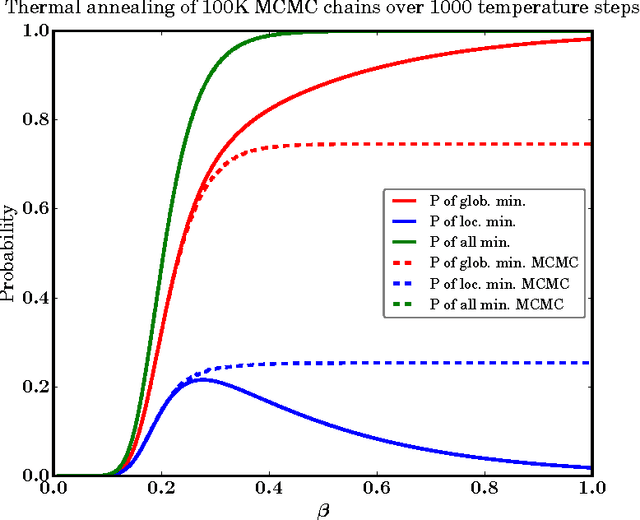
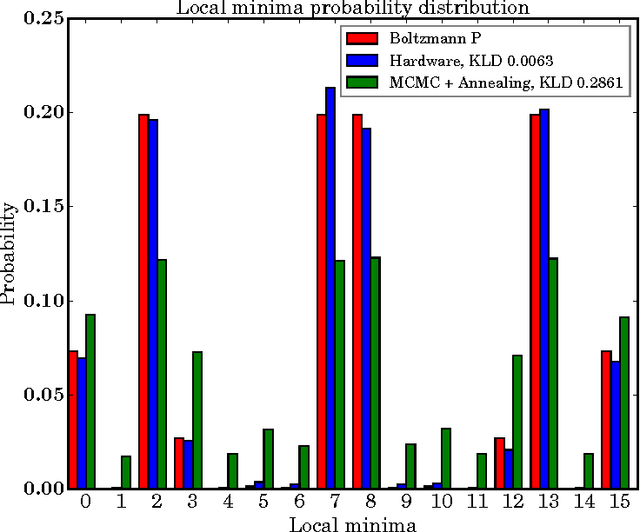
Quantum annealing (QA) is a hardware-based heuristic optimization and sampling method applicable to discrete undirected graphical models. While similar to simulated annealing, QA relies on quantum, rather than thermal, effects to explore complex search spaces. For many classes of problems, QA is known to offer computational advantages over simulated annealing. Here we report on the ability of recent QA hardware to accelerate training of fully visible Boltzmann machines. We characterize the sampling distribution of QA hardware, and show that in many cases, the quantum distributions differ significantly from classical Boltzmann distributions. In spite of this difference, training (which seeks to match data and model statistics) using standard classical gradient updates is still effective. We investigate the use of QA for seeding Markov chains as an alternative to contrastive divergence (CD) and persistent contrastive divergence (PCD). Using $k=50$ Gibbs steps, we show that for problems with high-energy barriers between modes, QA-based seeds can improve upon chains with CD and PCD initializations. For these hard problems, QA gradient estimates are more accurate, and allow for faster learning. Furthermore, and interestingly, even the case of raw QA samples (that is, $k=0$) achieved similar improvements. We argue that this relates to the fact that we are training a quantum rather than classical Boltzmann distribution in this case. The learned parameters give rise to hardware QA distributions closely approximating classical Boltzmann distributions that are hard to train with CD/PCD.

Understanding Deep Architectures using a Recursive Convolutional Network

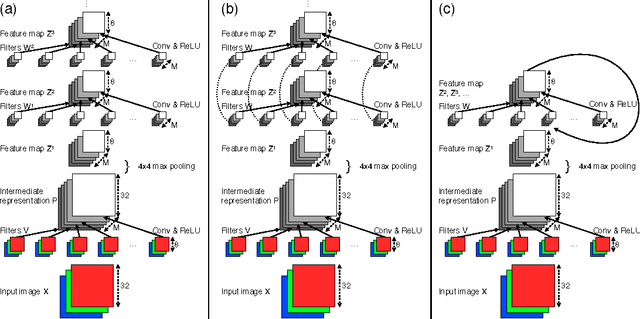
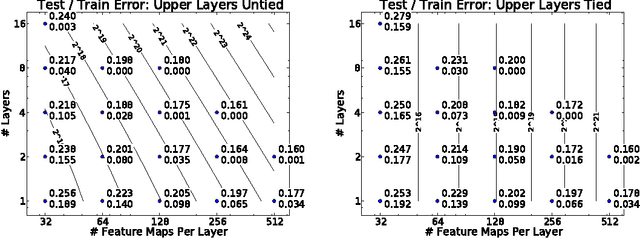
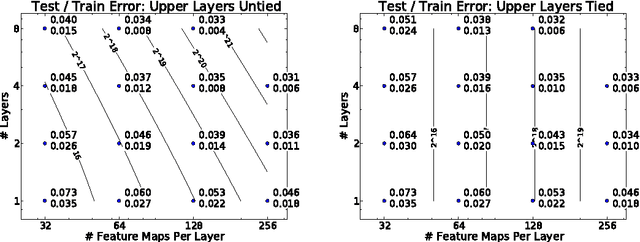
A key challenge in designing convolutional network models is sizing them appropriately. Many factors are involved in these decisions, including number of layers, feature maps, kernel sizes, etc. Complicating this further is the fact that each of these influence not only the numbers and dimensions of the activation units, but also the total number of parameters. In this paper we focus on assessing the independent contributions of three of these linked variables: The numbers of layers, feature maps, and parameters. To accomplish this, we employ a recursive convolutional network whose weights are tied between layers; this allows us to vary each of the three factors in a controlled setting. We find that while increasing the numbers of layers and parameters each have clear benefit, the number of feature maps (and hence dimensionality of the representation) appears ancillary, and finds most of its benefit through the introduction of more weights. Our results (i) empirically confirm the notion that adding layers alone increases computational power, within the context of convolutional layers, and (ii) suggest that precise sizing of convolutional feature map dimensions is itself of little concern; more attention should be paid to the number of parameters in these layers instead.