Neural-Guided RuntimePrediction of Planners for Improved Motion and Task Planning with Graph Neural Networks

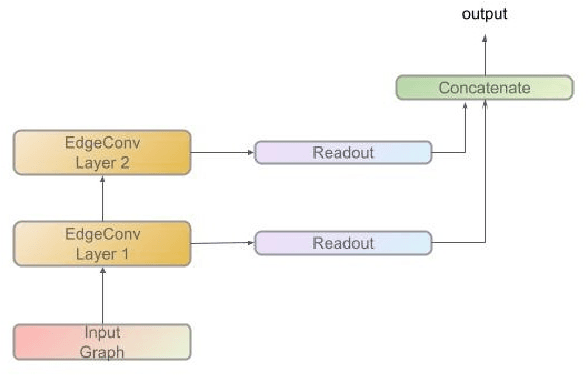
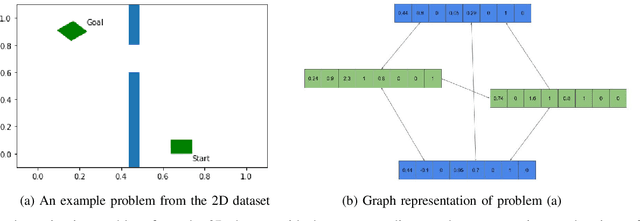
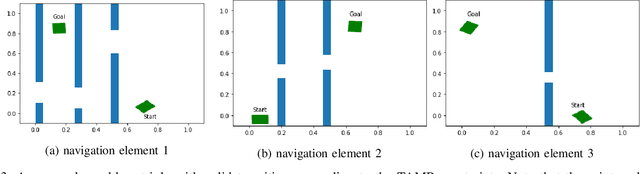
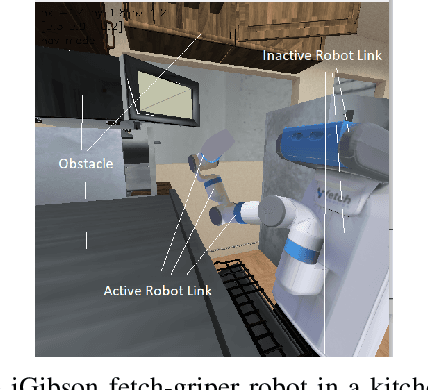
The past decade has amply demonstrated the remarkable functionality that can be realized by learning complex input/output relationships. Algorithmically, one of the most important and opaque relationships is that between a problem's structure and an effective solution method. Here, we quantitatively connect the structure of a planning problem to the performance of a given sampling-based motion planning (SBMP) algorithm. We demonstrate that the geometric relationships of motion planning problems can be well captured by graph neural networks (GNNs) to predict SBMP runtime. By using an algorithm portfolio we show that GNN predictions of runtime on particular problems can be leveraged to accelerate online motion planning in both navigation and manipulation tasks. Moreover, the problem-to-runtime map can be inverted to identify subproblems easier to solve by particular SBMPs. We provide a motivating example of how this knowledge may be used to improve integrated task and motion planning on simulated examples. These successes rely on the relational structure of GNNs to capture scalable generalization from low-dimensional navigation tasks to high degree-of-freedom manipulation tasks in 3d environments.

A Robust Learning Approach to Domain Adaptive Object Detection

Domain shift is unavoidable in real-world applications of object detection. For example, in self-driving cars, the target domain consists of unconstrained road environments which cannot all possibly be observed in training data. Similarly, in surveillance applications sufficiently representative training data may be lacking due to privacy regulations. In this paper, we address the domain adaptation problem from the perspective of robust learning and show that the problem may be formulated as training with noisy labels. We propose a robust object detection framework that is resilient to noise in bounding box class labels, locations and size annotations. To adapt to the domain shift, the model is trained on the target domain using a set of noisy object bounding boxes that are obtained by a detection model trained only in the source domain. We evaluate the accuracy of our approach in various source/target domain pairs and demonstrate that the model significantly improves the state-of-the-art on multiple domain adaptation scenarios on the SIM10K, Cityscapes and KITTI datasets.

Learning Undirected Posteriors by Backpropagation through MCMC Updates

The representation of the posterior is a critical aspect of effective variational autoencoders (VAEs). Poor choices for the posterior have a detrimental impact on the generative performance of VAEs due to the mismatch with the true posterior. We extend the class of posterior models that may be learned by using undirected graphical models. We develop an efficient method to train undirected posteriors by showing that the gradient of the training objective with respect to the parameters of the undirected posterior can be computed by backpropagation through Markov chain Monte Carlo updates. We apply these gradient estimators for training discrete VAEs with Boltzmann machine posteriors and demonstrate that undirected models outperform previous results obtained using directed graphical models as posteriors.

Weakly Supervised Semantic Image Segmentation with Self-correcting Networks

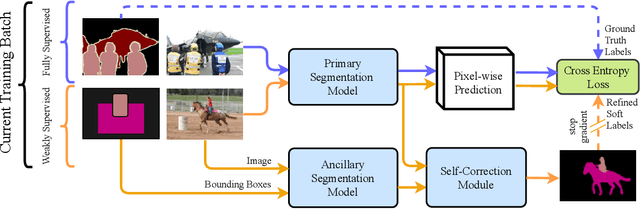
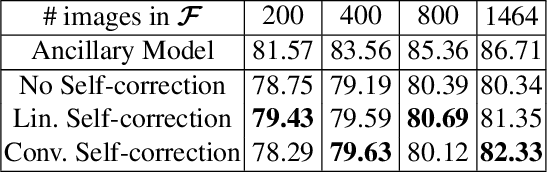
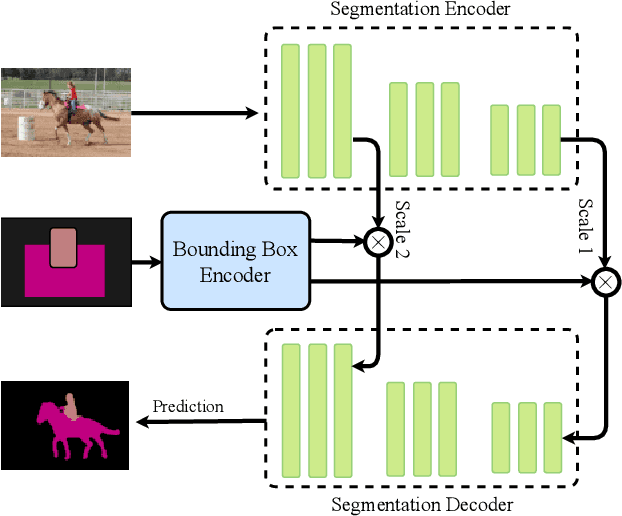
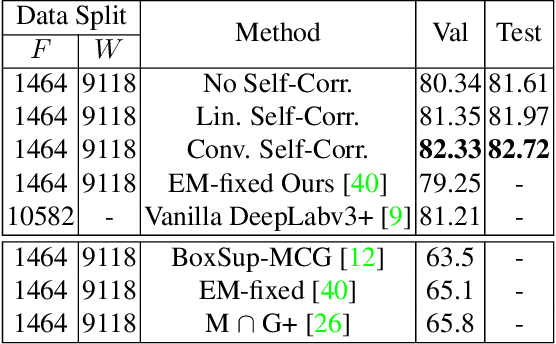
Building a large image dataset with high-quality object masks for semantic segmentation is costly and time consuming. In this paper, we reduce the data preparation cost by leveraging weak supervision in the form of object bounding boxes. To accomplish this, we propose a principled framework that trains a deep convolutional segmentation model that combines a large set of weakly supervised images (having only object bounding box labels) with a small set of fully supervised images (having semantic segmentation labels and box labels). Our framework trains the primary segmentation model with the aid of an ancillary model that generates initial segmentation labels for the weakly supervised instances and a self-correction module that improves the generated labels during training using the increasingly accurate primary model. We introduce two variants of the self-correction module using either linear or convolutional functions. Experiments on the PASCAL VOC 2012 and Cityscape datasets show that our models trained with a small fully supervised set perform similar to, or better than, models trained with a large fully supervised set while requiring ~7x less annotation effort.

DVAE#: Discrete Variational Autoencoders with Relaxed Boltzmann Priors

Boltzmann machines are powerful distributions that have been shown to be an effective prior over binary latent variables in variational autoencoders (VAEs). However, previous methods for training discrete VAEs have used the evidence lower bound and not the tighter importance-weighted bound. We propose two approaches for relaxing Boltzmann machines to continuous distributions that permit training with importance-weighted bounds. These relaxations are based on generalized overlapping transformations and the Gaussian integral trick. Experiments on the MNIST and OMNIGLOT datasets show that these relaxations outperform previous discrete VAEs with Boltzmann priors. An implementation which reproduces these results is available at https://github.com/QuadrantAI/dvae .

DVAE++: Discrete Variational Autoencoders with Overlapping Transformations

Training of discrete latent variable models remains challenging because passing gradient information through discrete units is difficult. We propose a new class of smoothing transformations based on a mixture of two overlapping distributions, and show that the proposed transformation can be used for training binary latent models with either directed or undirected priors. We derive a new variational bound to efficiently train with Boltzmann machine priors. Using this bound, we develop DVAE++, a generative model with a global discrete prior and a hierarchy of convolutional continuous variables. Experiments on several benchmarks show that overlapping transformations outperform other recent continuous relaxations of discrete latent variables including Gumbel-Softmax (Maddison et al., 2016; Jang et al., 2016), and discrete variational autoencoders (Rolfe 2016).

Benchmarking Quantum Hardware for Training of Fully Visible Boltzmann Machines

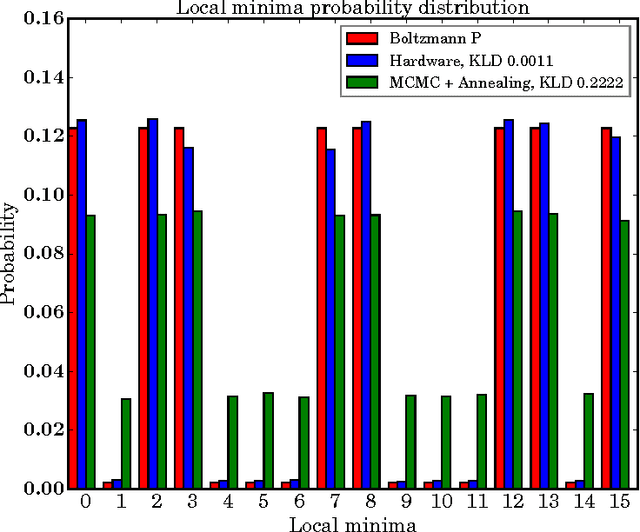
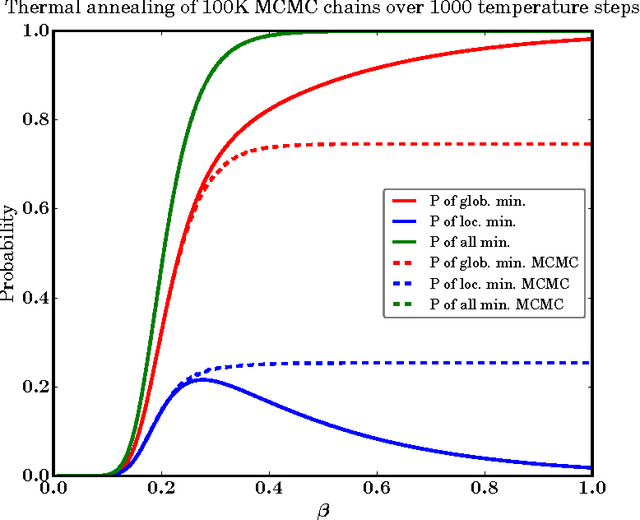
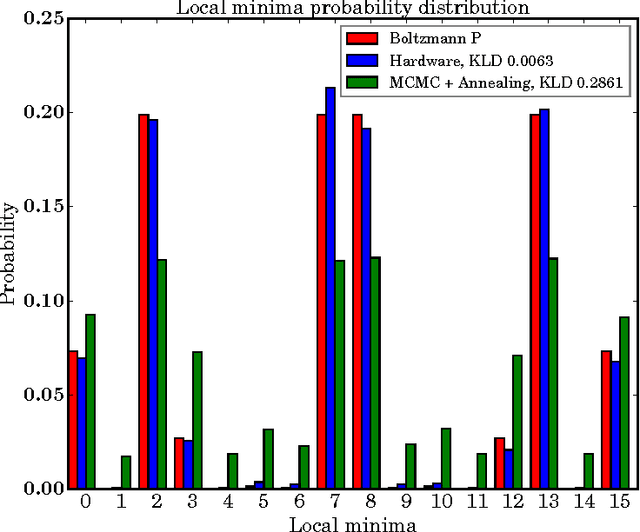
Quantum annealing (QA) is a hardware-based heuristic optimization and sampling method applicable to discrete undirected graphical models. While similar to simulated annealing, QA relies on quantum, rather than thermal, effects to explore complex search spaces. For many classes of problems, QA is known to offer computational advantages over simulated annealing. Here we report on the ability of recent QA hardware to accelerate training of fully visible Boltzmann machines. We characterize the sampling distribution of QA hardware, and show that in many cases, the quantum distributions differ significantly from classical Boltzmann distributions. In spite of this difference, training (which seeks to match data and model statistics) using standard classical gradient updates is still effective. We investigate the use of QA for seeding Markov chains as an alternative to contrastive divergence (CD) and persistent contrastive divergence (PCD). Using $k=50$ Gibbs steps, we show that for problems with high-energy barriers between modes, QA-based seeds can improve upon chains with CD and PCD initializations. For these hard problems, QA gradient estimates are more accurate, and allow for faster learning. Furthermore, and interestingly, even the case of raw QA samples (that is, $k=0$) achieved similar improvements. We argue that this relates to the fact that we are training a quantum rather than classical Boltzmann distribution in this case. The learned parameters give rise to hardware QA distributions closely approximating classical Boltzmann distributions that are hard to train with CD/PCD.

Training a Large Scale Classifier with the Quantum Adiabatic Algorithm

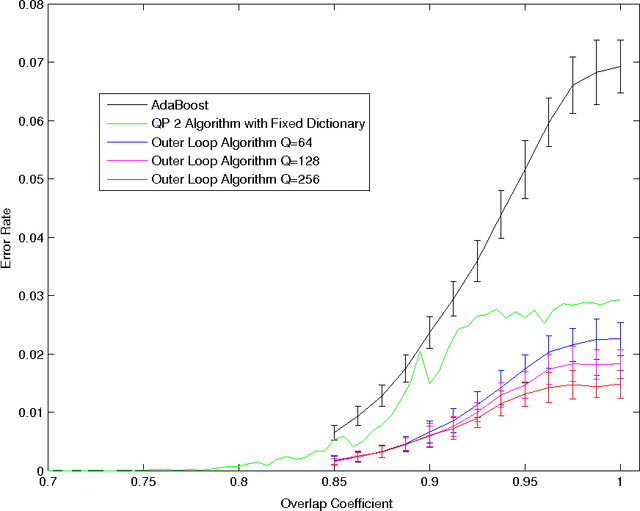
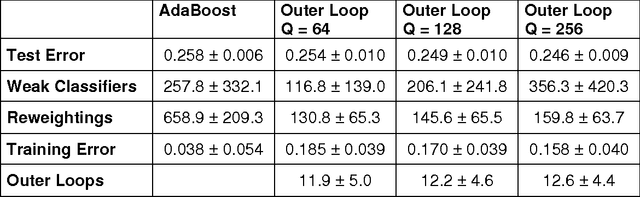
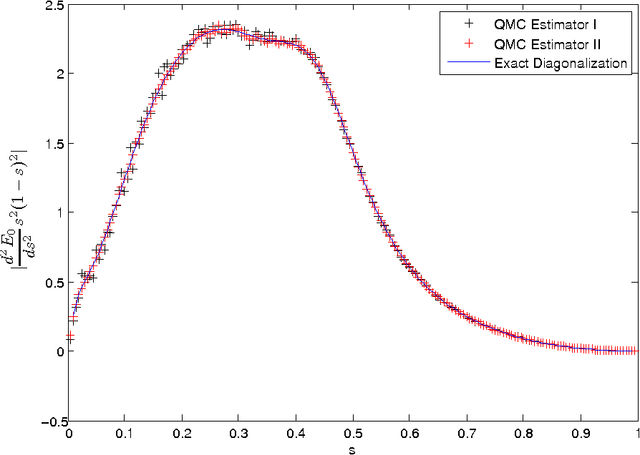
In a previous publication we proposed discrete global optimization as a method to train a strong binary classifier constructed as a thresholded sum over weak classifiers. Our motivation was to cast the training of a classifier into a format amenable to solution by the quantum adiabatic algorithm. Applying adiabatic quantum computing (AQC) promises to yield solutions that are superior to those which can be achieved with classical heuristic solvers. Interestingly we found that by using heuristic solvers to obtain approximate solutions we could already gain an advantage over the standard method AdaBoost. In this communication we generalize the baseline method to large scale classifier training. By large scale we mean that either the cardinality of the dictionary of candidate weak classifiers or the number of weak learners used in the strong classifier exceed the number of variables that can be handled effectively in a single global optimization. For such situations we propose an iterative and piecewise approach in which a subset of weak classifiers is selected in each iteration via global optimization. The strong classifier is then constructed by concatenating the subsets of weak classifiers. We show in numerical studies that the generalized method again successfully competes with AdaBoost. We also provide theoretical arguments as to why the proposed optimization method, which does not only minimize the empirical loss but also adds L0-norm regularization, is superior to versions of boosting that only minimize the empirical loss. By conducting a Quantum Monte Carlo simulation we gather evidence that the quantum adiabatic algorithm is able to handle a generic training problem efficiently.