Neural-Guided RuntimePrediction of Planners for Improved Motion and Task Planning with Graph Neural Networks
Paper and Code
Jul 29, 2022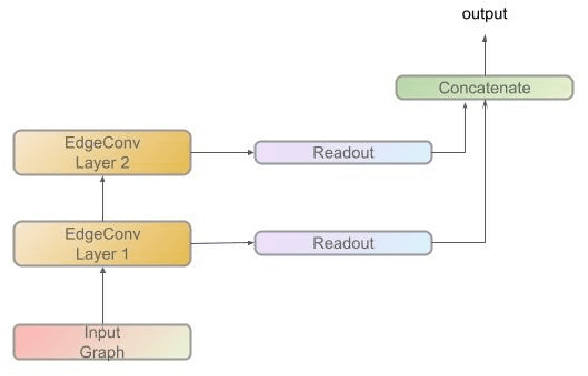
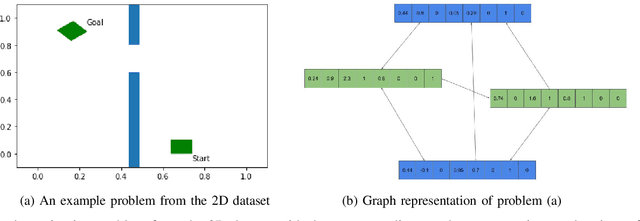
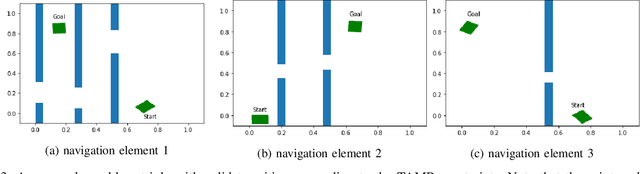
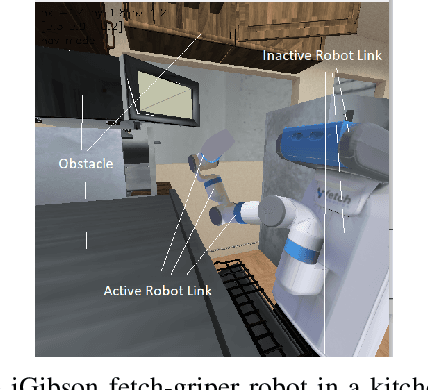
The past decade has amply demonstrated the remarkable functionality that can be realized by learning complex input/output relationships. Algorithmically, one of the most important and opaque relationships is that between a problem's structure and an effective solution method. Here, we quantitatively connect the structure of a planning problem to the performance of a given sampling-based motion planning (SBMP) algorithm. We demonstrate that the geometric relationships of motion planning problems can be well captured by graph neural networks (GNNs) to predict SBMP runtime. By using an algorithm portfolio we show that GNN predictions of runtime on particular problems can be leveraged to accelerate online motion planning in both navigation and manipulation tasks. Moreover, the problem-to-runtime map can be inverted to identify subproblems easier to solve by particular SBMPs. We provide a motivating example of how this knowledge may be used to improve integrated task and motion planning on simulated examples. These successes rely on the relational structure of GNNs to capture scalable generalization from low-dimensional navigation tasks to high degree-of-freedom manipulation tasks in 3d environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge