A Semantic Framework for Neural-Symbolic Computing

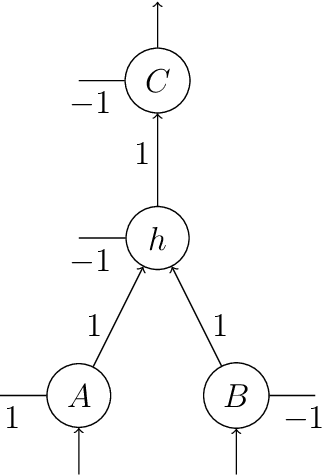
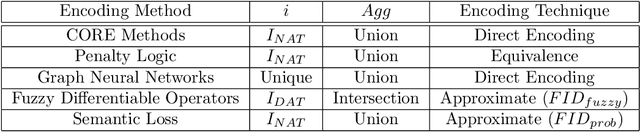
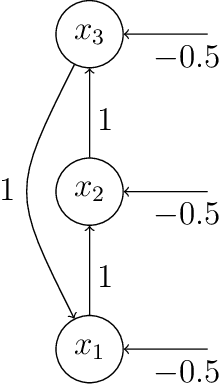
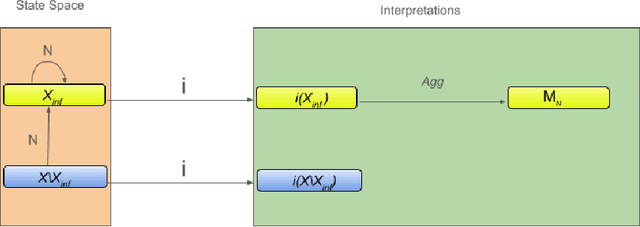
Two approaches to AI, neural networks and symbolic systems, have been proven very successful for an array of AI problems. However, neither has been able to achieve the general reasoning ability required for human-like intelligence. It has been argued that this is due to inherent weaknesses in each approach. Luckily, these weaknesses appear to be complementary, with symbolic systems being adept at the kinds of things neural networks have trouble with and vice-versa. The field of neural-symbolic AI attempts to exploit this asymmetry by combining neural networks and symbolic AI into integrated systems. Often this has been done by encoding symbolic knowledge into neural networks. Unfortunately, although many different methods for this have been proposed, there is no common definition of an encoding to compare them. We seek to rectify this problem by introducing a semantic framework for neural-symbolic AI, which is then shown to be general enough to account for a large family of neural-symbolic systems. We provide a number of examples and proofs of the application of the framework to the neural encoding of various forms of knowledge representation and neural network. These, at first sight disparate approaches, are all shown to fall within the framework's formal definition of what we call semantic encoding for neural-symbolic AI.

Neural-Guided RuntimePrediction of Planners for Improved Motion and Task Planning with Graph Neural Networks

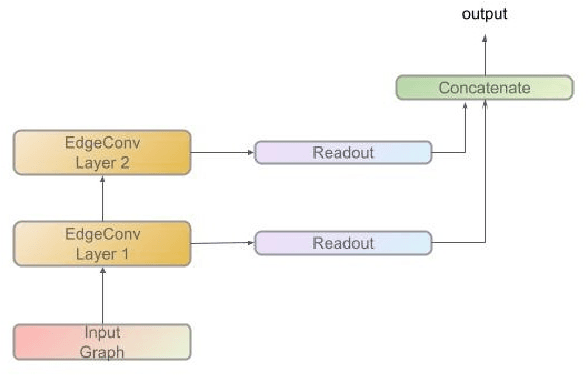
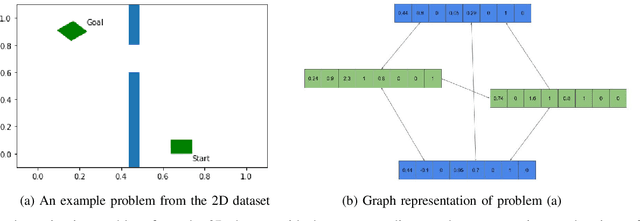
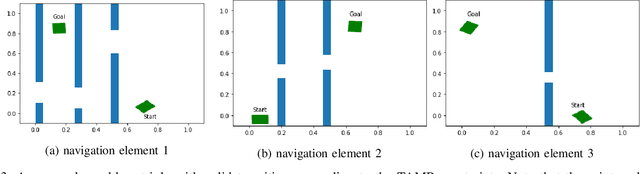
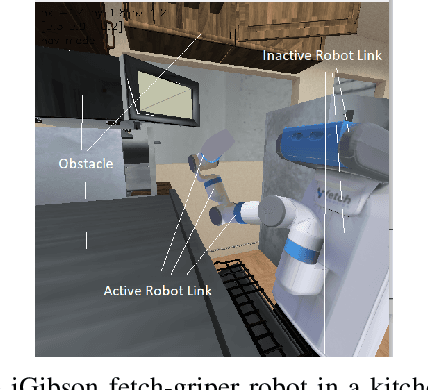
The past decade has amply demonstrated the remarkable functionality that can be realized by learning complex input/output relationships. Algorithmically, one of the most important and opaque relationships is that between a problem's structure and an effective solution method. Here, we quantitatively connect the structure of a planning problem to the performance of a given sampling-based motion planning (SBMP) algorithm. We demonstrate that the geometric relationships of motion planning problems can be well captured by graph neural networks (GNNs) to predict SBMP runtime. By using an algorithm portfolio we show that GNN predictions of runtime on particular problems can be leveraged to accelerate online motion planning in both navigation and manipulation tasks. Moreover, the problem-to-runtime map can be inverted to identify subproblems easier to solve by particular SBMPs. We provide a motivating example of how this knowledge may be used to improve integrated task and motion planning on simulated examples. These successes rely on the relational structure of GNNs to capture scalable generalization from low-dimensional navigation tasks to high degree-of-freedom manipulation tasks in 3d environments.

Layerwise Knowledge Extraction from Deep Convolutional Networks

Knowledge extraction is used to convert neural networks into symbolic descriptions with the objective of producing more comprehensible learning models. The central challenge is to find an explanation which is more comprehensible than the original model while still representing that model faithfully. The distributed nature of deep networks has led many to believe that the hidden features of a neural network cannot be explained by logical descriptions simple enough to be comprehensible. In this paper, we propose a novel layerwise knowledge extraction method using M-of-N rules which seeks to obtain the best trade-off between the complexity and accuracy of rules describing the hidden features of a deep network. We show empirically that this approach produces rules close to an optimal complexity-error tradeoff. We apply this method to a variety of deep networks and find that in the internal layers we often cannot find rules with a satisfactory complexity and accuracy, suggesting that rule extraction as a general purpose method for explaining the internal logic of a neural network may be impossible. However, we also find that the softmax layer in Convolutional Neural Networks and Autoencoders using either tanh or relu activation functions is highly explainable by rule extraction, with compact rules consisting of as little as 3 units out of 128 often reaching over 99% accuracy. This shows that rule extraction can be a useful component for explaining parts (or modules) of a deep neural network.