Totally Corrective Boosting with Cardinality Penalization

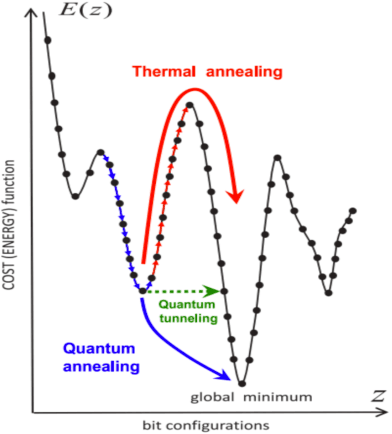
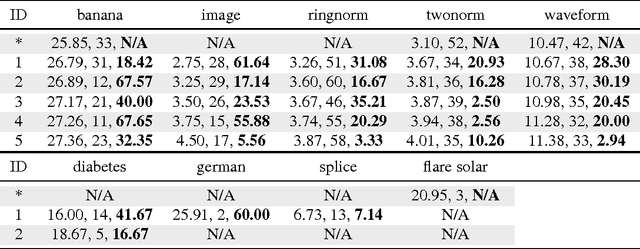
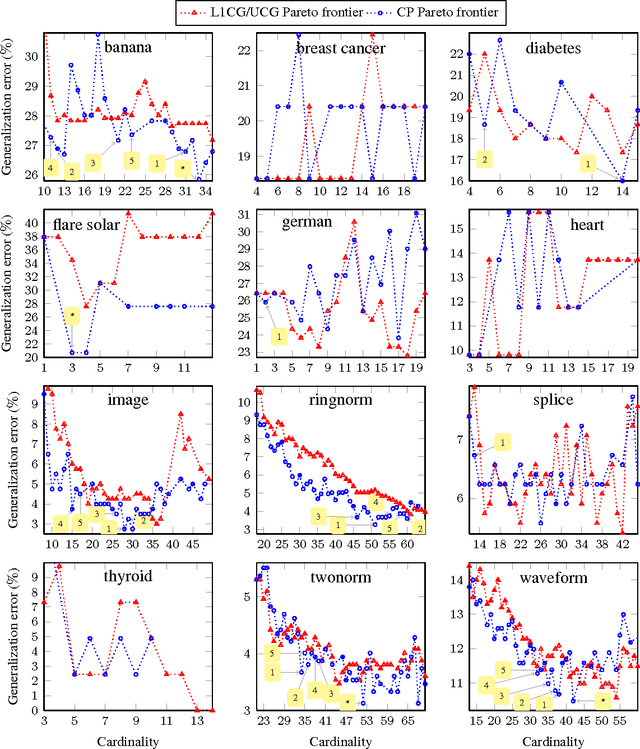
We propose a totally corrective boosting algorithm with explicit cardinality regularization. The resulting combinatorial optimization problems are not known to be efficiently solvable with existing classical methods, but emerging quantum optimization technology gives hope for achieving sparser models in practice. In order to demonstrate the utility of our algorithm, we use a distributed classical heuristic optimizer as a stand-in for quantum hardware. Even though this evaluation methodology incurs large time and resource costs on classical computing machinery, it allows us to gauge the potential gains in generalization performance and sparsity of the resulting boosted ensembles. Our experimental results on public data sets commonly used for benchmarking of boosting algorithms decidedly demonstrate the existence of such advantages. If actual quantum optimization were to be used with this algorithm in the future, we would expect equivalent or superior results at much smaller time and energy costs during training. Moreover, studying cardinality-penalized boosting also sheds light on why unregularized boosting algorithms with early stopping often yield better results than their counterparts with explicit convex regularization: Early stopping performs suboptimal cardinality regularization. The results that we present here indicate it is beneficial to explicitly solve the combinatorial problem still left open at early termination.

Training a Large Scale Classifier with the Quantum Adiabatic Algorithm

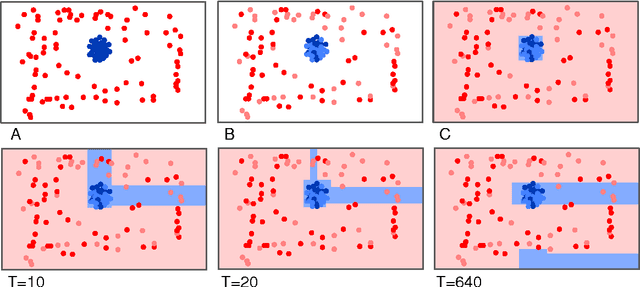
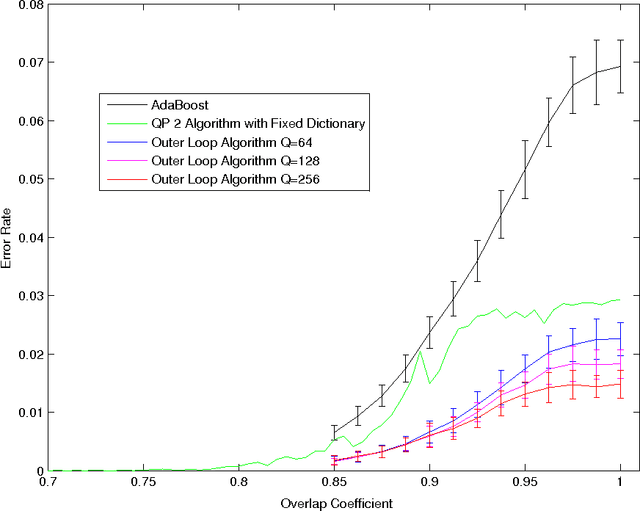
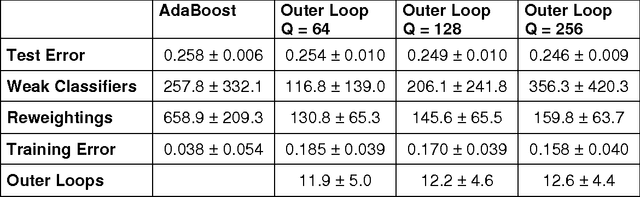
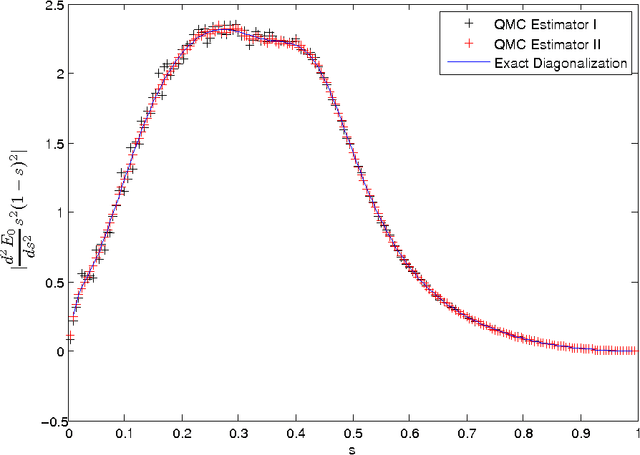
In a previous publication we proposed discrete global optimization as a method to train a strong binary classifier constructed as a thresholded sum over weak classifiers. Our motivation was to cast the training of a classifier into a format amenable to solution by the quantum adiabatic algorithm. Applying adiabatic quantum computing (AQC) promises to yield solutions that are superior to those which can be achieved with classical heuristic solvers. Interestingly we found that by using heuristic solvers to obtain approximate solutions we could already gain an advantage over the standard method AdaBoost. In this communication we generalize the baseline method to large scale classifier training. By large scale we mean that either the cardinality of the dictionary of candidate weak classifiers or the number of weak learners used in the strong classifier exceed the number of variables that can be handled effectively in a single global optimization. For such situations we propose an iterative and piecewise approach in which a subset of weak classifiers is selected in each iteration via global optimization. The strong classifier is then constructed by concatenating the subsets of weak classifiers. We show in numerical studies that the generalized method again successfully competes with AdaBoost. We also provide theoretical arguments as to why the proposed optimization method, which does not only minimize the empirical loss but also adds L0-norm regularization, is superior to versions of boosting that only minimize the empirical loss. By conducting a Quantum Monte Carlo simulation we gather evidence that the quantum adiabatic algorithm is able to handle a generic training problem efficiently.