Totally Corrective Boosting with Cardinality Penalization
Paper and Code
Apr 07, 2015
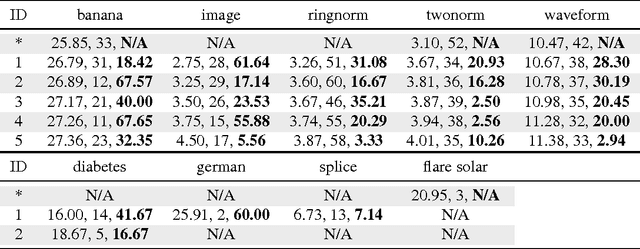

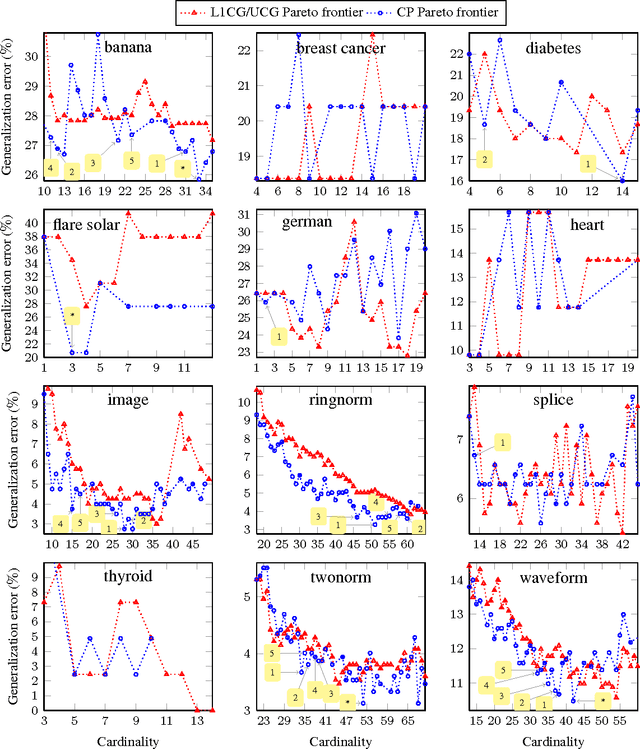
We propose a totally corrective boosting algorithm with explicit cardinality regularization. The resulting combinatorial optimization problems are not known to be efficiently solvable with existing classical methods, but emerging quantum optimization technology gives hope for achieving sparser models in practice. In order to demonstrate the utility of our algorithm, we use a distributed classical heuristic optimizer as a stand-in for quantum hardware. Even though this evaluation methodology incurs large time and resource costs on classical computing machinery, it allows us to gauge the potential gains in generalization performance and sparsity of the resulting boosted ensembles. Our experimental results on public data sets commonly used for benchmarking of boosting algorithms decidedly demonstrate the existence of such advantages. If actual quantum optimization were to be used with this algorithm in the future, we would expect equivalent or superior results at much smaller time and energy costs during training. Moreover, studying cardinality-penalized boosting also sheds light on why unregularized boosting algorithms with early stopping often yield better results than their counterparts with explicit convex regularization: Early stopping performs suboptimal cardinality regularization. The results that we present here indicate it is beneficial to explicitly solve the combinatorial problem still left open at early termination.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge