Detection of Unobserved Common Causes based on NML Code in Discrete, Mixed, and Continuous Variables

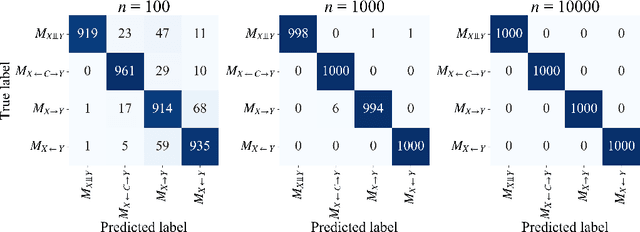
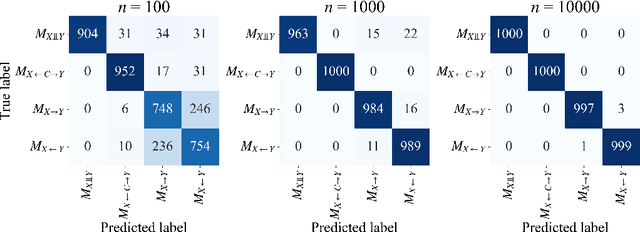
Causal discovery in the presence of unobserved common causes from observational data only is a crucial but challenging problem. We categorize all possible causal relationships between two random variables into the following four categories and aim to identify one from observed data: two cases in which either of the direct causality exists, a case that variables are independent, and a case that variables are confounded by latent confounders. Although existing methods have been proposed to tackle this problem, they require unobserved variables to satisfy assumptions on the form of their equation models. In our previous study (Kobayashi et al., 2022), the first causal discovery method without such assumptions is proposed for discrete data and named CLOUD. Using Normalized Maximum Likelihood (NML) Code, CLOUD selects a model that yields the minimum codelength of the observed data from a set of model candidates. This paper extends CLOUD to apply for various data types across discrete, mixed, and continuous. We not only performed theoretical analysis to show the consistency of CLOUD in terms of the model selection, but also demonstrated that CLOUD is more effective than existing methods in inferring causal relationships by extensive experiments on both synthetic and real-world data.

mdx: A Cloud Platform for Supporting Data Science and Cross-Disciplinary Research Collaborations

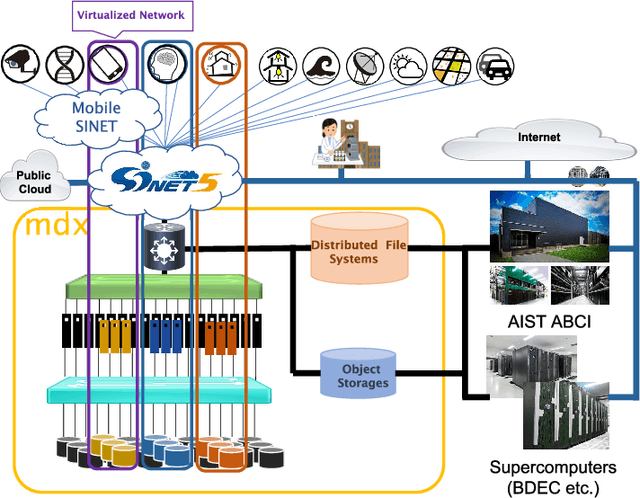
The growing amount of data and advances in data science have created a need for a new kind of cloud platform that provides users with flexibility, strong security, and the ability to couple with supercomputers and edge devices through high-performance networks. We have built such a nation-wide cloud platform, called "mdx" to meet this need. The mdx platform's virtualization service, jointly operated by 9 national universities and 2 national research institutes in Japan, launched in 2021, and more features are in development. Currently mdx is used by researchers in a wide variety of domains, including materials informatics, geo-spatial information science, life science, astronomical science, economics, social science, and computer science. This paper provides an the overview of the mdx platform, details the motivation for its development, reports its current status, and outlines its future plans.

DS-MLR: Exploiting Double Separability for Scaling up Distributed Multinomial Logistic Regression

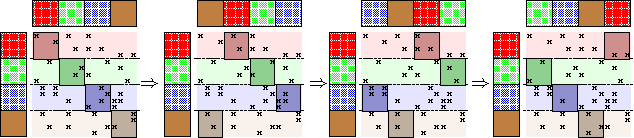
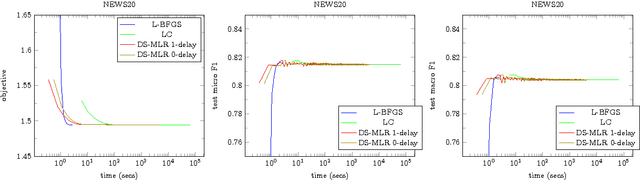
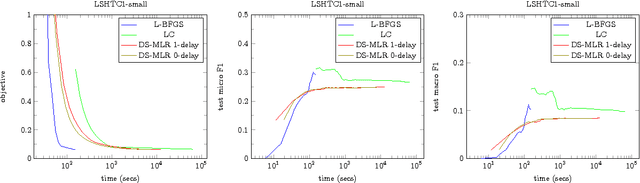
Scaling multinomial logistic regression to datasets with very large number of data points and classes is challenging. This is primarily because one needs to compute the log-partition function on every data point. This makes distributing the computation hard. In this paper, we present a distributed stochastic gradient descent based optimization method (DS-MLR) for scaling up multinomial logistic regression problems to massive scale datasets without hitting any storage constraints on the data and model parameters. Our algorithm exploits double-separability, an attractive property that allows us to achieve both data as well as model parallelism simultaneously. In addition, we introduce a non-blocking and asynchronous variant of our algorithm that avoids bulk-synchronization. We demonstrate the versatility of DS-MLR to various scenarios in data and model parallelism, through an extensive empirical study using several real-world datasets. In particular, we demonstrate the scalability of DS-MLR by solving an extreme multi-class classification problem on the Reddit dataset (159 GB data, 358 GB parameters) where, to the best of our knowledge, no other existing methods apply.

Statistical Learnability of Generalized Additive Models based on Total Variation Regularization

A generalized additive model (GAM, Hastie and Tibshirani (1987)) is a nonparametric model by the sum of univariate functions with respect to each explanatory variable, i.e., $f({\mathbf x}) = \sum f_j(x_j)$, where $x_j\in\mathbb{R}$ is $j$-th component of a sample ${\mathbf x}\in \mathbb{R}^p$. In this paper, we introduce the total variation (TV) of a function as a measure of the complexity of functions in $L^1_{\rm c}(\mathbb{R})$-space. Our analysis shows that a GAM based on TV-regularization exhibits a Rademacher complexity of $O(\sqrt{\frac{\log p}{m}})$, which is tight in terms of both $m$ and $p$ in the agnostic case of the classification problem. In result, we obtain generalization error bounds for finite samples according to work by Bartlett and Mandelson (2002).

Grafting for Combinatorial Boolean Model using Frequent Itemset Mining

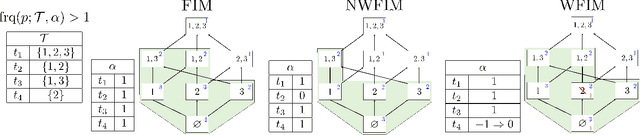
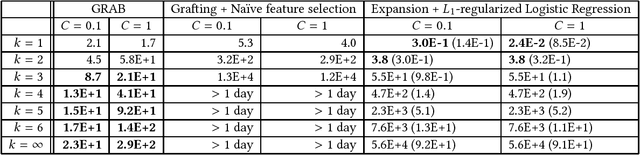
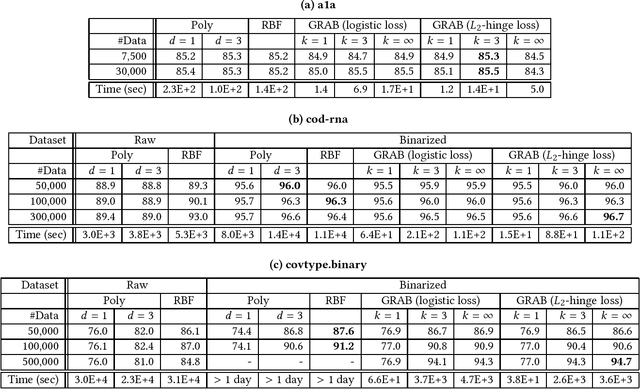
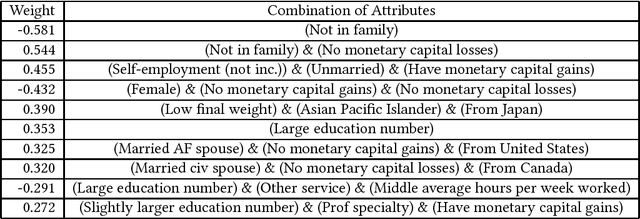
This paper introduces the combinatorial Boolean model (CBM), which is defined as the class of linear combinations of conjunctions of Boolean attributes. This paper addresses the issue of learning CBM from labeled data. CBM is of high knowledge interpretability but na\"{i}ve learning of it requires exponentially large computation time with respect to data dimension and sample size. To overcome this computational difficulty, we propose an algorithm GRAB (GRAfting for Boolean datasets), which efficiently learns CBM within the $L_1$-regularized loss minimization framework. The key idea of GRAB is to reduce the loss minimization problem to the weighted frequent itemset mining, in which frequent patterns are efficiently computable. We employ benchmark datasets to empirically demonstrate that GRAB is effective in terms of computational efficiency, prediction accuracy and knowledge discovery.

WordRank: Learning Word Embeddings via Robust Ranking

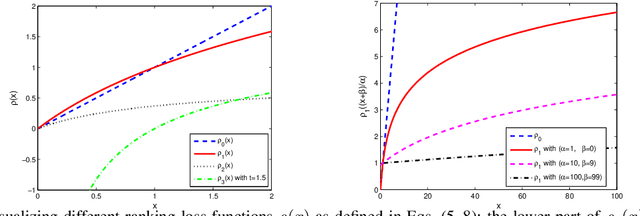
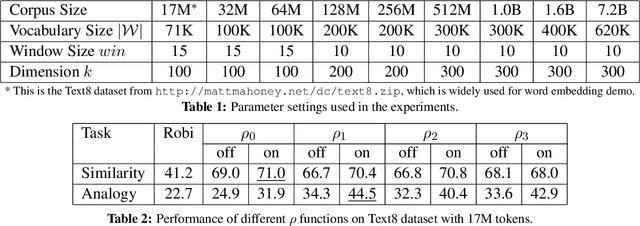
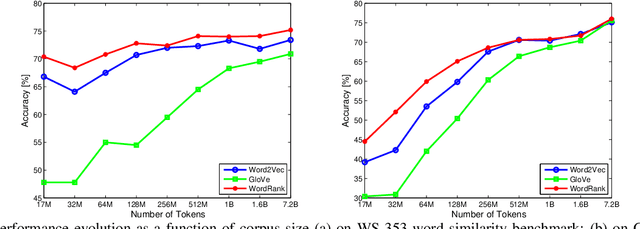
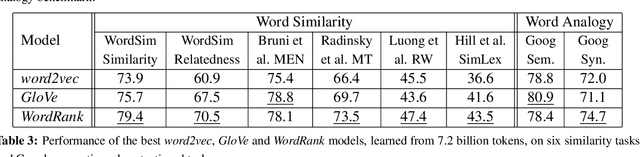
Embedding words in a vector space has gained a lot of attention in recent years. While state-of-the-art methods provide efficient computation of word similarities via a low-dimensional matrix embedding, their motivation is often left unclear. In this paper, we argue that word embedding can be naturally viewed as a ranking problem due to the ranking nature of the evaluation metrics. Then, based on this insight, we propose a novel framework WordRank that efficiently estimates word representations via robust ranking, in which the attention mechanism and robustness to noise are readily achieved via the DCG-like ranking losses. The performance of WordRank is measured in word similarity and word analogy benchmarks, and the results are compared to the state-of-the-art word embedding techniques. Our algorithm is very competitive to the state-of-the- arts on large corpora, while outperforms them by a significant margin when the training set is limited (i.e., sparse and noisy). With 17 million tokens, WordRank performs almost as well as existing methods using 7.2 billion tokens on a popular word similarity benchmark. Our multi-node distributed implementation of WordRank is publicly available for general usage.

Distributed Stochastic Optimization of the Regularized Risk

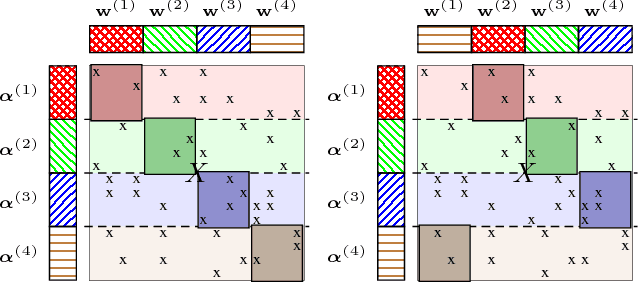
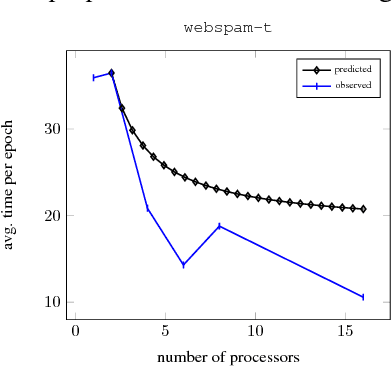
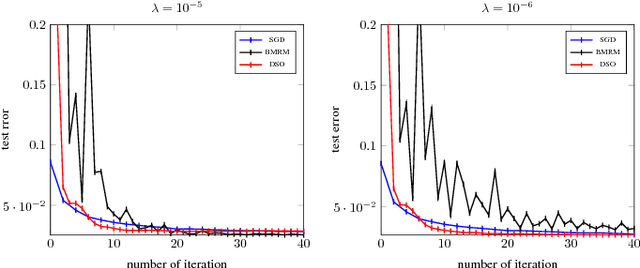
Many machine learning algorithms minimize a regularized risk, and stochastic optimization is widely used for this task. When working with massive data, it is desirable to perform stochastic optimization in parallel. Unfortunately, many existing stochastic optimization algorithms cannot be parallelized efficiently. In this paper we show that one can rewrite the regularized risk minimization problem as an equivalent saddle-point problem, and propose an efficient distributed stochastic optimization (DSO) algorithm. We prove the algorithm's rate of convergence; remarkably, our analysis shows that the algorithm scales almost linearly with the number of processors. We also verify with empirical evaluations that the proposed algorithm is competitive with other parallel, general purpose stochastic and batch optimization algorithms for regularized risk minimization.

Totally Corrective Boosting with Cardinality Penalization

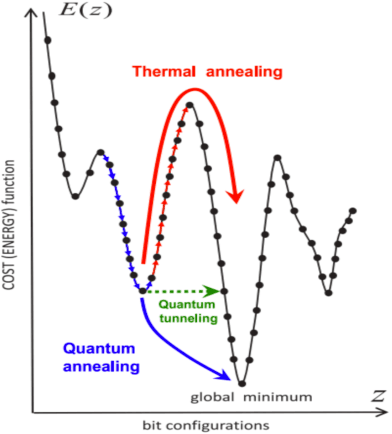
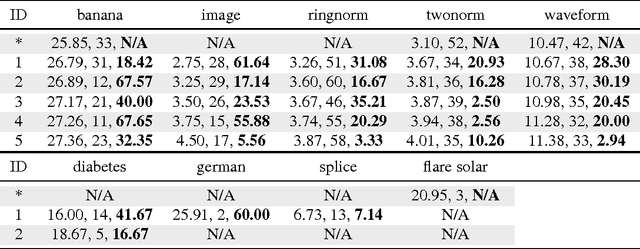
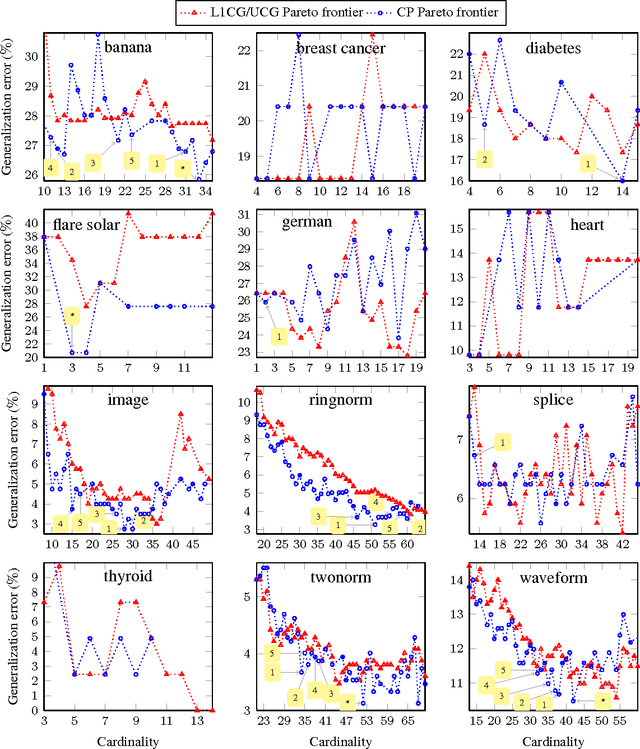
We propose a totally corrective boosting algorithm with explicit cardinality regularization. The resulting combinatorial optimization problems are not known to be efficiently solvable with existing classical methods, but emerging quantum optimization technology gives hope for achieving sparser models in practice. In order to demonstrate the utility of our algorithm, we use a distributed classical heuristic optimizer as a stand-in for quantum hardware. Even though this evaluation methodology incurs large time and resource costs on classical computing machinery, it allows us to gauge the potential gains in generalization performance and sparsity of the resulting boosted ensembles. Our experimental results on public data sets commonly used for benchmarking of boosting algorithms decidedly demonstrate the existence of such advantages. If actual quantum optimization were to be used with this algorithm in the future, we would expect equivalent or superior results at much smaller time and energy costs during training. Moreover, studying cardinality-penalized boosting also sheds light on why unregularized boosting algorithms with early stopping often yield better results than their counterparts with explicit convex regularization: Early stopping performs suboptimal cardinality regularization. The results that we present here indicate it is beneficial to explicitly solve the combinatorial problem still left open at early termination.