Kohei Miyagichi
Detection of Unobserved Common Causes based on NML Code in Discrete, Mixed, and Continuous Variables
Mar 11, 2024
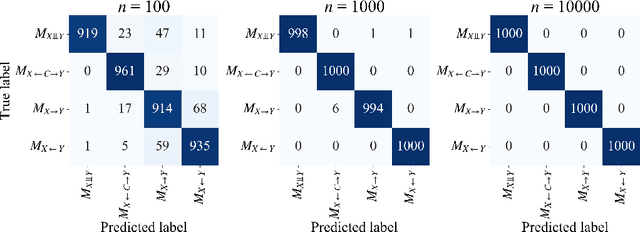

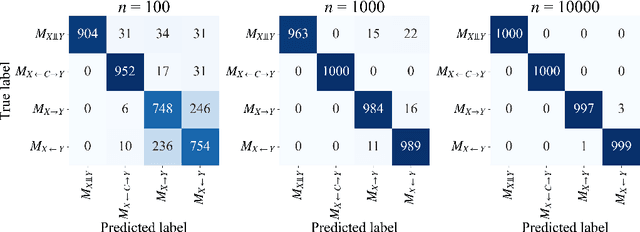
Abstract:Causal discovery in the presence of unobserved common causes from observational data only is a crucial but challenging problem. We categorize all possible causal relationships between two random variables into the following four categories and aim to identify one from observed data: two cases in which either of the direct causality exists, a case that variables are independent, and a case that variables are confounded by latent confounders. Although existing methods have been proposed to tackle this problem, they require unobserved variables to satisfy assumptions on the form of their equation models. In our previous study (Kobayashi et al., 2022), the first causal discovery method without such assumptions is proposed for discrete data and named CLOUD. Using Normalized Maximum Likelihood (NML) Code, CLOUD selects a model that yields the minimum codelength of the observed data from a set of model candidates. This paper extends CLOUD to apply for various data types across discrete, mixed, and continuous. We not only performed theoretical analysis to show the consistency of CLOUD in terms of the model selection, but also demonstrated that CLOUD is more effective than existing methods in inferring causal relationships by extensive experiments on both synthetic and real-world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge