Optimal Low-Depth Quantum Signal-Processing Phase Estimation

Quantum effects like entanglement and coherent amplification can be used to drastically enhance the accuracy of quantum parameter estimation beyond classical limits. However, challenges such as decoherence and time-dependent errors hinder Heisenberg-limited amplification. We introduce Quantum Signal-Processing Phase Estimation algorithms that are robust against these challenges and achieve optimal performance as dictated by the Cram\'{e}r-Rao bound. These algorithms use quantum signal transformation to decouple interdependent phase parameters into largely orthogonal ones, ensuring that time-dependent errors in one do not compromise the accuracy of learning the other. Combining provably optimal classical estimation with near-optimal quantum circuit design, our approach achieves an unprecedented standard deviation accuracy of $10^{-4}$ radians for estimating unwanted swap angles in superconducting two-qubit experiments, using low-depth ($<10$) circuits. This represents up to two orders of magnitude improvement over existing methods. Theoretically and numerically, we demonstrate the optimality of our algorithm against time-dependent phase errors, observing that the variance of the time-sensitive parameter $\varphi$ scales faster than the asymptotic Heisenberg scaling in the small-depth regime. Our results are rigorously validated against the quantum Fisher information, confirming our protocol's ability to achieve unmatched precision for two-qubit gate learning.

Learning to Decode the Surface Code with a Recurrent, Transformer-Based Neural Network

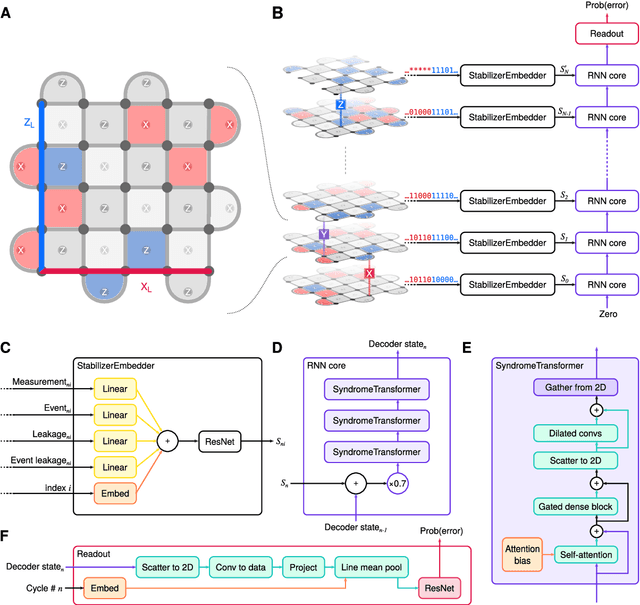
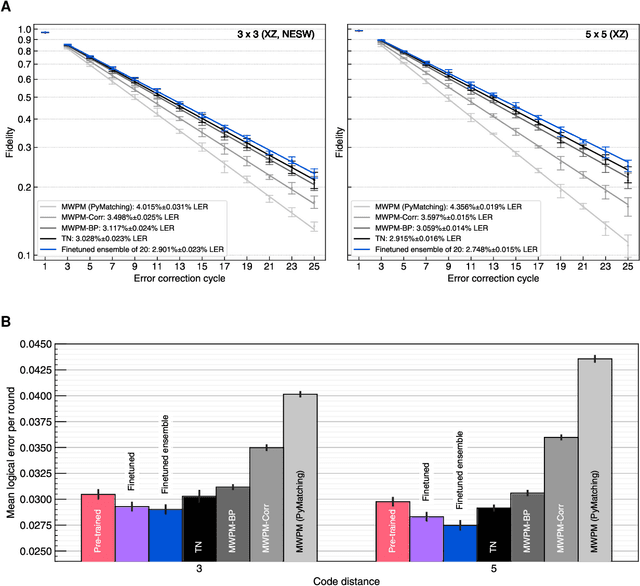
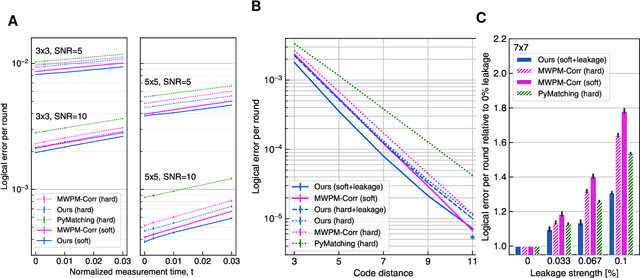
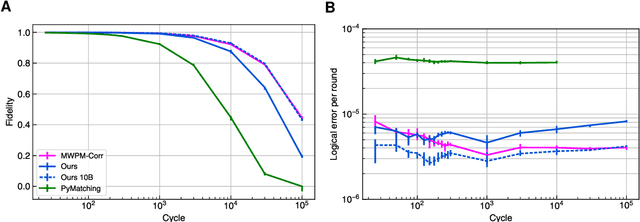
Quantum error-correction is a prerequisite for reliable quantum computation. Towards this goal, we present a recurrent, transformer-based neural network which learns to decode the surface code, the leading quantum error-correction code. Our decoder outperforms state-of-the-art algorithmic decoders on real-world data from Google's Sycamore quantum processor for distance 3 and 5 surface codes. On distances up to 11, the decoder maintains its advantage on simulated data with realistic noise including cross-talk, leakage, and analog readout signals, and sustains its accuracy far beyond the 25 cycles it was trained on. Our work illustrates the ability of machine learning to go beyond human-designed algorithms by learning from data directly, highlighting machine learning as a strong contender for decoding in quantum computers.

Beyond Heisenberg Limit Quantum Metrology through Quantum Signal Processing

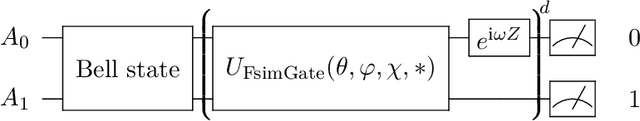
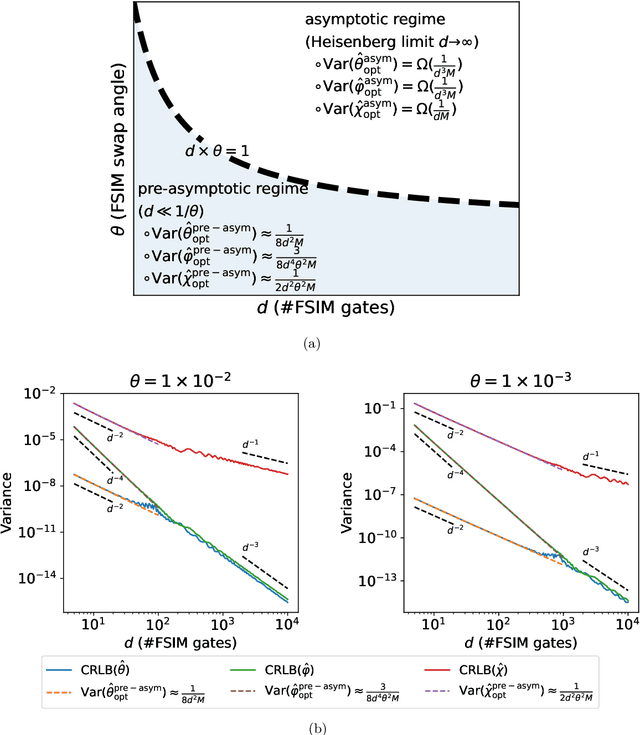
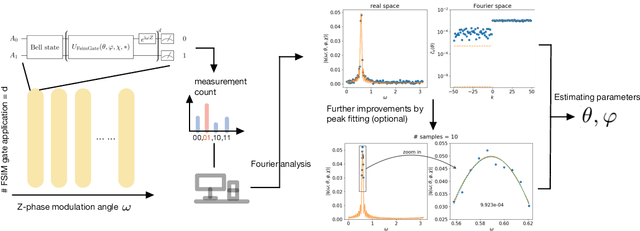
Leveraging quantum effects in metrology such as entanglement and coherence allows one to measure parameters with enhanced sensitivity. However, time-dependent noise can disrupt such Heisenberg-limited amplification. We propose a quantum-metrology method based on the quantum-signal-processing framework to overcome these realistic noise-induced limitations in practical quantum metrology. Our algorithm separates the gate parameter $\varphi$~(single-qubit Z phase) that is susceptible to time-dependent error from the target gate parameter $\theta$~(swap-angle between |10> and |01> states) that is largely free of time-dependent error. Our method achieves an accuracy of $10^{-4}$ radians in standard deviation for learning $\theta$ in superconducting-qubit experiments, outperforming existing alternative schemes by two orders of magnitude. We also demonstrate the increased robustness in learning time-dependent gate parameters through fast Fourier transformation and sequential phase difference. We show both theoretically and numerically that there is an interesting transition of the optimal metrology variance scaling as a function of circuit depth $d$ from the pre-asymptotic regime $d \ll 1/\theta$ to Heisenberg limit $d \to \infty$. Remarkably, in the pre-asymptotic regime our method's estimation variance on time-sensitive parameter $\varphi$ scales faster than the asymptotic Heisenberg limit as a function of depth, $\text{Var}(\hat{\varphi})\approx 1/d^4$. Our work is the first quantum-signal-processing algorithm that demonstrates practical application in laboratory quantum computers.

Learnability and Complexity of Quantum Samples

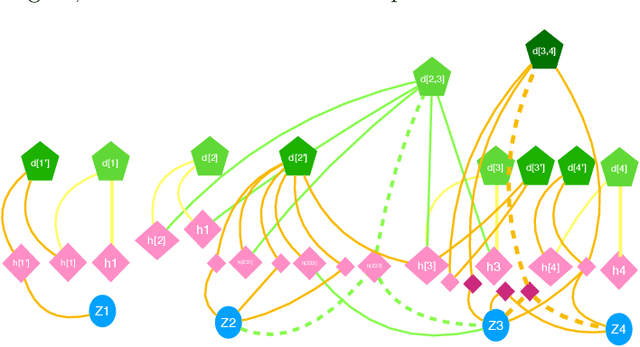
Given a quantum circuit, a quantum computer can sample the output distribution exponentially faster in the number of bits than classical computers. A similar exponential separation has yet to be established in generative models through quantum sample learning: given samples from an n-qubit computation, can we learn the underlying quantum distribution using models with training parameters that scale polynomial in n under a fixed training time? We study four kinds of generative models: Deep Boltzmann machine (DBM), Generative Adversarial Networks (GANs), Long Short-Term Memory (LSTM) and Autoregressive GAN, on learning quantum data set generated by deep random circuits. We demonstrate the leading performance of LSTM in learning quantum samples, and thus the autoregressive structure present in the underlying quantum distribution from random quantum circuits. Both numerical experiments and a theoretical proof in the case of the DBM show exponentially growing complexity of learning-agent parameters required for achieving a fixed accuracy as n increases. Finally, we establish a connection between learnability and the complexity of generative models by benchmarking learnability against different sets of samples drawn from probability distributions of variable degrees of complexities in their quantum and classical representations.

TensorFlow Quantum: A Software Framework for Quantum Machine Learning

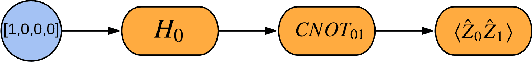
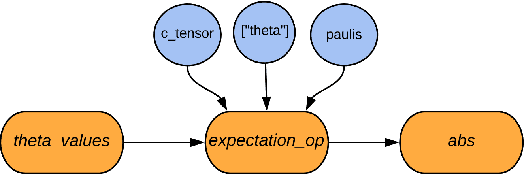
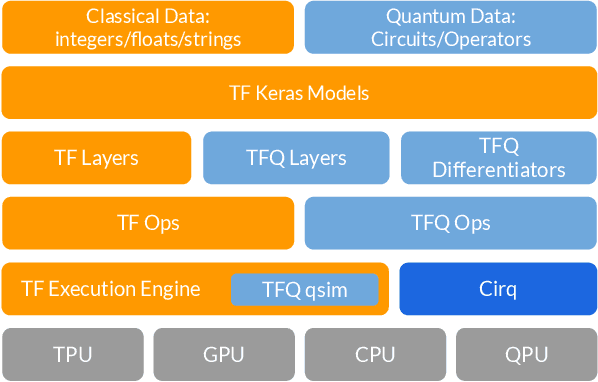
We introduce TensorFlow Quantum (TFQ), an open source library for the rapid prototyping of hybrid quantum-classical models for classical or quantum data. This framework offers high-level abstractions for the design and training of both discriminative and generative quantum models under TensorFlow and supports high-performance quantum circuit simulators. We provide an overview of the software architecture and building blocks through several examples and review the theory of hybrid quantum-classical neural networks. We illustrate TFQ functionalities via several basic applications including supervised learning for quantum classification, quantum control, and quantum approximate optimization. Moreover, we demonstrate how one can apply TFQ to tackle advanced quantum learning tasks including meta-learning, Hamiltonian learning, and sampling thermal states. We hope this framework provides the necessary tools for the quantum computing and machine learning research communities to explore models of both natural and artificial quantum systems, and ultimately discover new quantum algorithms which could potentially yield a quantum advantage.

Learning Non-Markovian Quantum Noise from Moiré-Enhanced Swap Spectroscopy with Deep Evolutionary Algorithm

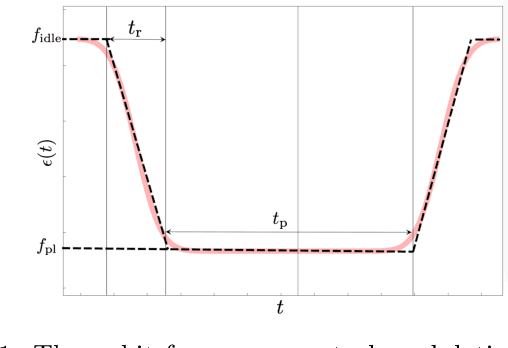
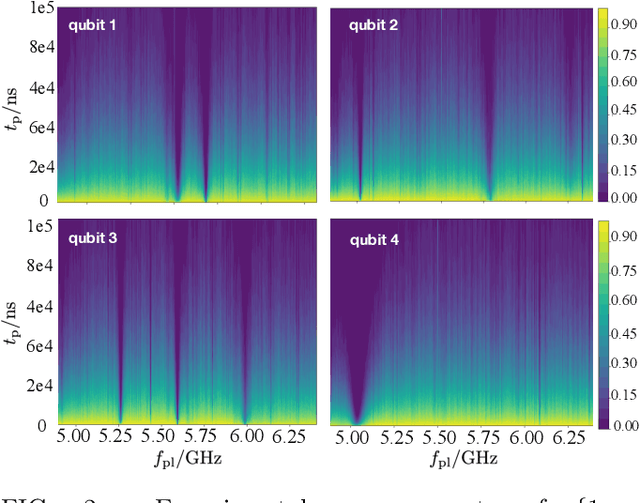
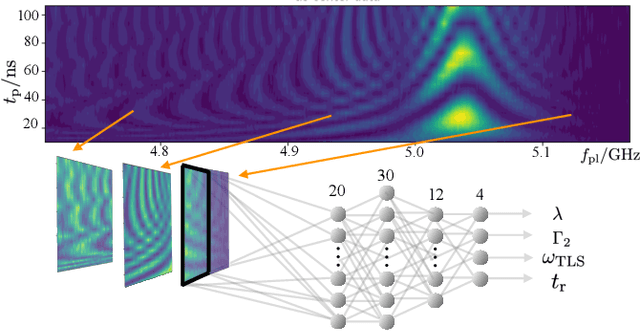
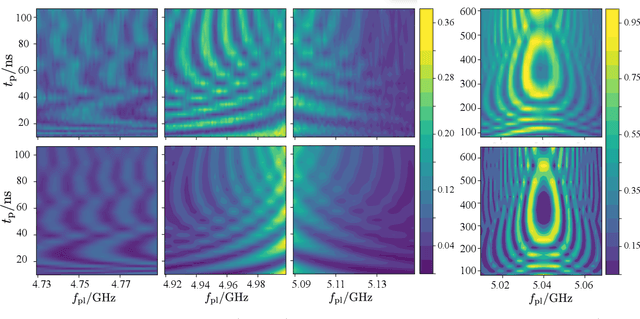
Two-level-system (TLS) defects in amorphous dielectrics are a major source of noise and decoherence in solid-state qubits. Gate-dependent non-Markovian errors caused by TLS-qubit coupling are detrimental to fault-tolerant quantum computation and have not been rigorously treated in the existing literature. In this work, we derive the non-Markovian dynamics between TLS and qubits during a SWAP-like two-qubit gate and the associated average gate fidelity for frequency-tunable Transmon qubits. This gate dependent error model facilitates using qubits as sensors to simultaneously learn practical imperfections in both the qubit's environment and control waveforms. We combine the-state-of-art machine learning algorithm with Moir\'{e}-enhanced swap spectroscopy to achieve robust learning using noisy experimental data. Deep neural networks are used to represent the functional map from experimental data to TLS parameters and are trained through an evolutionary algorithm. Our method achieves the highest learning efficiency and robustness against experimental imperfections to-date, representing an important step towards in-situ quantum control optimization over environmental and control defects.

Recurrent Neural Networks in the Eye of Differential Equations

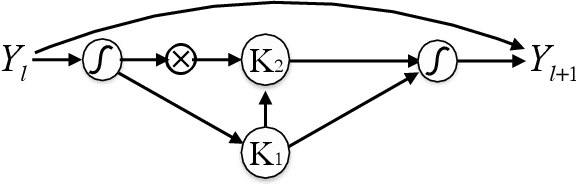
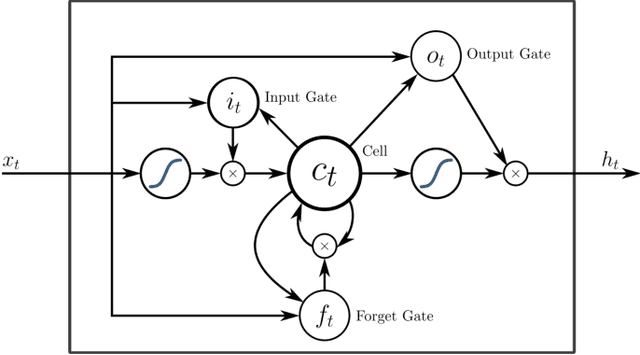
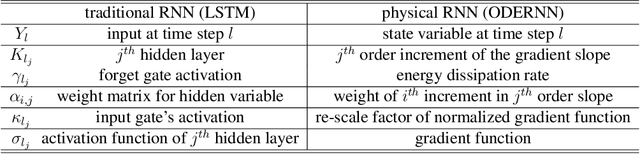
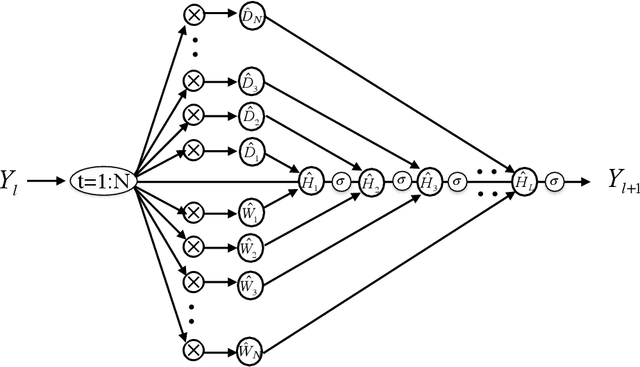
To understand the fundamental trade-offs between training stability, temporal dynamics and architectural complexity of recurrent neural networks~(RNNs), we directly analyze RNN architectures using numerical methods of ordinary differential equations~(ODEs). We define a general family of RNNs--the ODERNNs--by relating the composition rules of RNNs to integration methods of ODEs at discrete time steps. We show that the degree of RNN's functional nonlinearity $n$ and the range of its temporal memory $t$ can be mapped to the corresponding stage of Runge-Kutta recursion and the order of time-derivative of the ODEs. We prove that popular RNN architectures, such as LSTM and URNN, fit into different orders of $n$-$t$-ODERNNs. This exact correspondence between RNN and ODE helps us to establish the sufficient conditions for RNN training stability and facilitates more flexible top-down designs of new RNN architectures using large varieties of toolboxes from numerical integration of ODEs. We provide such an example: Quantum-inspired Universal computing Neural Network~(QUNN), which reduces the required number of training parameters from polynomial in both data length and temporal memory length to only linear in temporal memory length.