Recurrent Neural Networks in the Eye of Differential Equations
Paper and Code
Apr 29, 2019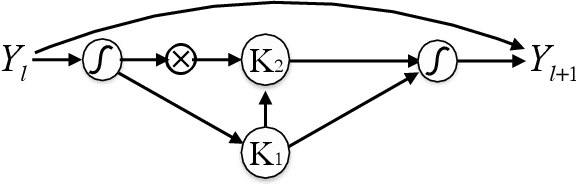
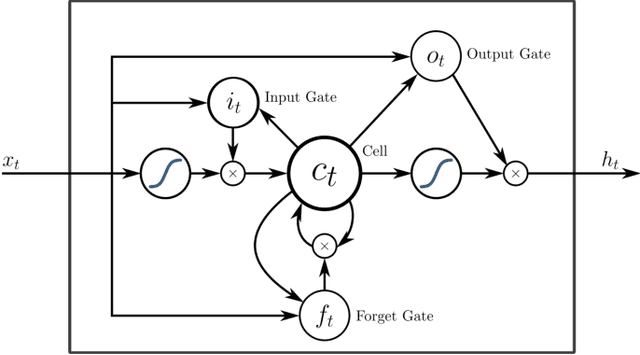
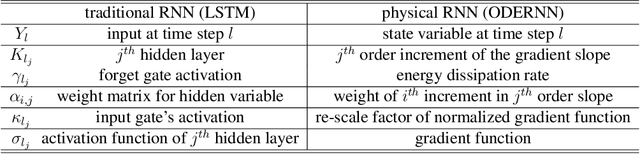
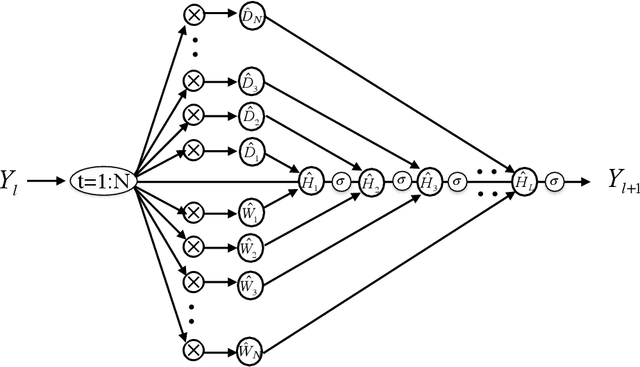
To understand the fundamental trade-offs between training stability, temporal dynamics and architectural complexity of recurrent neural networks~(RNNs), we directly analyze RNN architectures using numerical methods of ordinary differential equations~(ODEs). We define a general family of RNNs--the ODERNNs--by relating the composition rules of RNNs to integration methods of ODEs at discrete time steps. We show that the degree of RNN's functional nonlinearity $n$ and the range of its temporal memory $t$ can be mapped to the corresponding stage of Runge-Kutta recursion and the order of time-derivative of the ODEs. We prove that popular RNN architectures, such as LSTM and URNN, fit into different orders of $n$-$t$-ODERNNs. This exact correspondence between RNN and ODE helps us to establish the sufficient conditions for RNN training stability and facilitates more flexible top-down designs of new RNN architectures using large varieties of toolboxes from numerical integration of ODEs. We provide such an example: Quantum-inspired Universal computing Neural Network~(QUNN), which reduces the required number of training parameters from polynomial in both data length and temporal memory length to only linear in temporal memory length.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge