Neural Thermodynamics I: Entropic Forces in Deep and Universal Representation Learning

With the rapid discovery of emergent phenomena in deep learning and large language models, explaining and understanding their cause has become an urgent need. Here, we propose a rigorous entropic-force theory for understanding the learning dynamics of neural networks trained with stochastic gradient descent (SGD) and its variants. Building on the theory of parameter symmetries and an entropic loss landscape, we show that representation learning is crucially governed by emergent entropic forces arising from stochasticity and discrete-time updates. These forces systematically break continuous parameter symmetries and preserve discrete ones, leading to a series of gradient balance phenomena that resemble the equipartition property of thermal systems. These phenomena, in turn, (a) explain the universal alignment of neural representations between AI models and lead to a proof of the Platonic Representation Hypothesis, and (b) reconcile the seemingly contradictory observations of sharpness- and flatness-seeking behavior of deep learning optimization. Our theory and experiments demonstrate that a combination of entropic forces and symmetry breaking is key to understanding emergent phenomena in deep learning.

Heterosynaptic Circuits Are Universal Gradient Machines

We propose a design principle for the learning circuits of the biological brain. The principle states that almost any dendritic weights updated via heterosynaptic plasticity can implement a generalized and efficient class of gradient-based meta-learning. The theory suggests that a broad class of biologically plausible learning algorithms, together with the standard machine learning optimizers, can be grounded in heterosynaptic circuit motifs. This principle suggests that the phenomenology of (anti-) Hebbian (HBP) and heterosynaptic plasticity (HSP) may emerge from the same underlying dynamics, thus providing a unifying explanation. It also suggests an alternative perspective of neuroplasticity, where HSP is promoted to the primary learning and memory mechanism, and HBP is an emergent byproduct. We present simulations that show that (a) HSP can explain the metaplasticity of neurons, (b) HSP can explain the flexibility of the biology circuits, and (c) gradient learning can arise quickly from simple evolutionary dynamics that do not compute any explicit gradient. While our primary focus is on biology, the principle also implies a new approach to designing AI training algorithms and physically learnable AI hardware. Conceptually, our result demonstrates that contrary to the common belief, gradient computation may be extremely easy and common in nature.

Parameter Symmetry Breaking and Restoration Determines the Hierarchical Learning in AI Systems

The dynamics of learning in modern large AI systems is hierarchical, often characterized by abrupt, qualitative shifts akin to phase transitions observed in physical systems. While these phenomena hold promise for uncovering the mechanisms behind neural networks and language models, existing theories remain fragmented, addressing specific cases. In this paper, we posit that parameter symmetry breaking and restoration serve as a unifying mechanism underlying these behaviors. We synthesize prior observations and show how this mechanism explains three distinct hierarchies in neural networks: learning dynamics, model complexity, and representation formation. By connecting these hierarchies, we highlight symmetry -- a cornerstone of theoretical physics -- as a potential fundamental principle in modern AI.

Formation of Representations in Neural Networks

Understanding neural representations will help open the black box of neural networks and advance our scientific understanding of modern AI systems. However, how complex, structured, and transferable representations emerge in modern neural networks has remained a mystery. Building on previous results, we propose the Canonical Representation Hypothesis (CRH), which posits a set of six alignment relations to universally govern the formation of representations in most hidden layers of a neural network. Under the CRH, the latent representations (R), weights (W), and neuron gradients (G) become mutually aligned during training. This alignment implies that neural networks naturally learn compact representations, where neurons and weights are invariant to task-irrelevant transformations. We then show that the breaking of CRH leads to the emergence of reciprocal power-law relations between R, W, and G, which we refer to as the Polynomial Alignment Hypothesis (PAH). We present a minimal-assumption theory demonstrating that the balance between gradient noise and regularization is crucial for the emergence the canonical representation. The CRH and PAH lead to an exciting possibility of unifying major key deep learning phenomena, including neural collapse and the neural feature ansatz, in a single framework.

Remove Symmetries to Control Model Expressivity

When symmetry is present in the loss function, the model is likely to be trapped in a low-capacity state that is sometimes known as a "collapse." Being trapped in these low-capacity states can be a major obstacle to training across many scenarios where deep learning technology is applied. We first prove two concrete mechanisms through which symmetries lead to reduced capacities and ignored features during training. We then propose a simple and theoretically justified algorithm, syre, to remove almost all symmetry-induced low-capacity states in neural networks. The proposed method is shown to improve the training of neural networks in scenarios when this type of entrapment is especially a concern. A remarkable merit of the proposed method is that it is model-agnostic and does not require any knowledge of the symmetry.

Recurrent Neural Networks in the Eye of Differential Equations

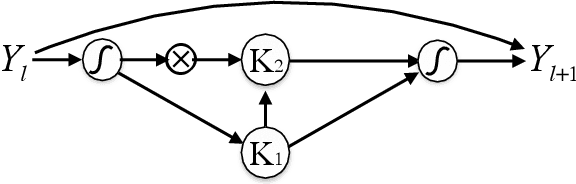
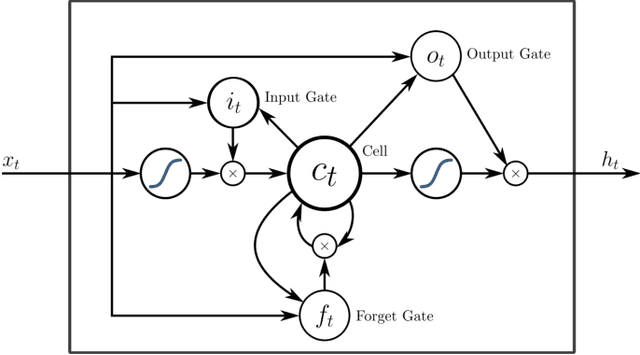
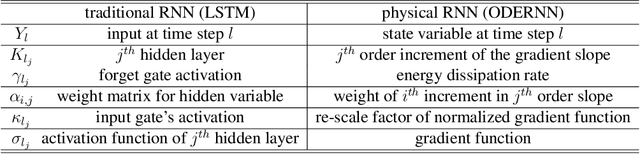
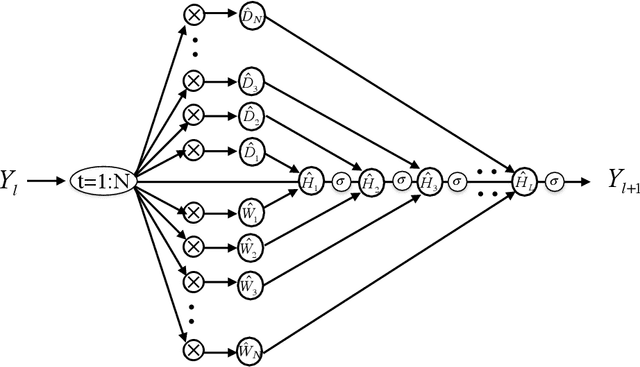
To understand the fundamental trade-offs between training stability, temporal dynamics and architectural complexity of recurrent neural networks~(RNNs), we directly analyze RNN architectures using numerical methods of ordinary differential equations~(ODEs). We define a general family of RNNs--the ODERNNs--by relating the composition rules of RNNs to integration methods of ODEs at discrete time steps. We show that the degree of RNN's functional nonlinearity $n$ and the range of its temporal memory $t$ can be mapped to the corresponding stage of Runge-Kutta recursion and the order of time-derivative of the ODEs. We prove that popular RNN architectures, such as LSTM and URNN, fit into different orders of $n$-$t$-ODERNNs. This exact correspondence between RNN and ODE helps us to establish the sufficient conditions for RNN training stability and facilitates more flexible top-down designs of new RNN architectures using large varieties of toolboxes from numerical integration of ODEs. We provide such an example: Quantum-inspired Universal computing Neural Network~(QUNN), which reduces the required number of training parameters from polynomial in both data length and temporal memory length to only linear in temporal memory length.