An Equivariance Toolbox for Learning Dynamics

Many theoretical results in deep learning can be traced to symmetry or equivariance of neural networks under parameter transformations. However, existing analyses are typically problem-specific and focus on first-order consequences such as conservation laws, while the implications for second-order structure remain less understood. We develop a general equivariance toolbox that yields coupled first- and second-order constraints on learning dynamics. The framework extends classical Noether-type analyses in three directions: from gradient constraints to Hessian constraints, from symmetry to general equivariance, and from continuous to discrete transformations. At the first order, our framework unifies conservation laws and implicit-bias relations as special cases of a single identity. At the second order, it provides structural predictions about curvature: which directions are flat or sharp, how the gradient aligns with Hessian eigenspaces, and how the loss landscape geometry reflects the underlying transformation structure. We illustrate the framework through several applications, recovering known results while also deriving new characterizations that connect transformation structure to modern empirical observations about optimization geometry.

When Reasoning Meets Its Laws

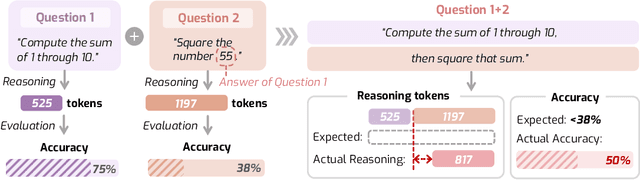
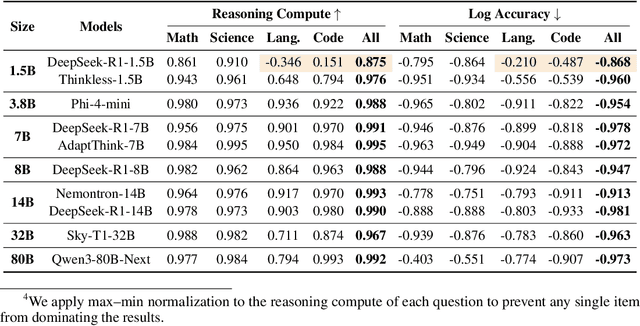
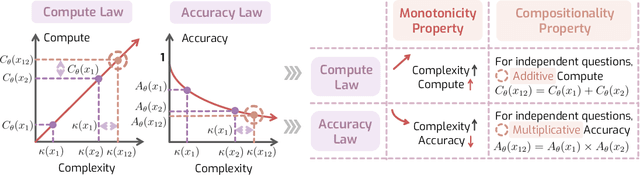
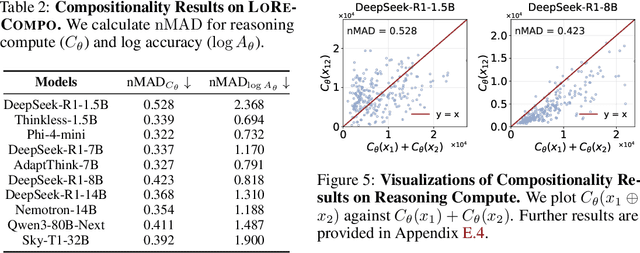
Despite the superior performance of Large Reasoning Models (LRMs), their reasoning behaviors are often counterintuitive, leading to suboptimal reasoning capabilities. To theoretically formalize the desired reasoning behaviors, this paper presents the Laws of Reasoning (LoRe), a unified framework that characterizes intrinsic reasoning patterns in LRMs. We first propose compute law with the hypothesis that the reasoning compute should scale linearly with question complexity. Beyond compute, we extend LoRe with a supplementary accuracy law. Since the question complexity is difficult to quantify in practice, we examine these hypotheses by two properties of the laws, monotonicity and compositionality. We therefore introduce LoRe-Bench, a benchmark that systematically measures these two tractable properties for large reasoning models. Evaluation shows that most reasoning models exhibit reasonable monotonicity but lack compositionality. In response, we develop an effective finetuning approach that enforces compute-law compositionality. Extensive empirical studies demonstrate that better compliance with compute laws yields consistently improved reasoning performance on multiple benchmarks, and uncovers synergistic effects across properties and laws. Project page: https://lore-project.github.io/

On Biologically Plausible Learning in Continuous Time

Biological learning unfolds continuously in time, yet most algorithmic models rely on discrete updates and separate inference and learning phases. We study a continuous-time neural model that unifies several biologically plausible learning algorithms and removes the need for phase separation. Rules including stochastic gradient descent (SGD), feedback alignment (FA), direct feedback alignment (DFA), and Kolen-Pollack (KP) emerge naturally as limiting cases of the dynamics. Simulations show that these continuous-time networks stably learn at biological timescales, even under temporal mismatches and integration noise. Through analysis and simulation, we show that learning depends on temporal overlap: a synapse updates correctly only when its input and the corresponding error signal coincide in time. When inputs are held constant, learning strength declines linearly as the delay between input and error approaches the stimulus duration, explaining observed robustness and failure across network depths. Critically, robust learning requires the synaptic plasticity timescale to exceed the stimulus duration by one to two orders of magnitude. For typical cortical stimuli (tens of milliseconds), this places the functional plasticity window in the few-second range, a testable prediction that identifies seconds-scale eligibility traces as necessary for error-driven learning in biological circuits.

A universal compression theory: Lottery ticket hypothesis and superpolynomial scaling laws

When training large-scale models, the performance typically scales with the number of parameters and the dataset size according to a slow power law. A fundamental theoretical and practical question is whether comparable performance can be achieved with significantly smaller models and substantially less data. In this work, we provide a positive and constructive answer. We prove that a generic permutation-invariant function of $d$ objects can be asymptotically compressed into a function of $\operatorname{polylog} d$ objects with vanishing error. This theorem yields two key implications: (Ia) a large neural network can be compressed to polylogarithmic width while preserving its learning dynamics; (Ib) a large dataset can be compressed to polylogarithmic size while leaving the loss landscape of the corresponding model unchanged. (Ia) directly establishes a proof of the \textit{dynamical} lottery ticket hypothesis, which states that any ordinary network can be strongly compressed such that the learning dynamics and result remain unchanged. (Ib) shows that a neural scaling law of the form $L\sim d^{-\alpha}$ can be boosted to an arbitrarily fast power law decay, and ultimately to $\exp(-\alpha' \sqrt[m]{d})$.

Proof of a perfect platonic representation hypothesis

In this note, we elaborate on and explain in detail the proof given by Ziyin et al. (2025) of the "perfect" Platonic Representation Hypothesis (PRH) for the embedded deep linear network model (EDLN). We show that if trained with SGD, two EDLNs with different widths and depths and trained on different data will become Perfectly Platonic, meaning that every possible pair of layers will learn the same representation up to a rotation. Because most of the global minima of the loss function are not Platonic, that SGD only finds the perfectly Platonic solution is rather extraordinary. The proof also suggests at least six ways the PRH can be broken. We also show that in the EDLN model, the emergence of the Platonic representations is due to the same reason as the emergence of progressive sharpening. This implies that these two seemingly unrelated phenomena in deep learning can, surprisingly, have a common cause. Overall, the theory and proof highlight the importance of understanding emergent "entropic forces" due to the irreversibility of SGD training and their role in representation learning. The goal of this note is to be instructive and avoid lengthy technical details.

Emergence of Hebbian Dynamics in Regularized Non-Local Learners

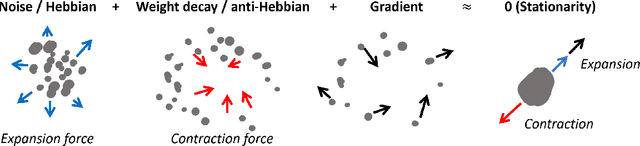
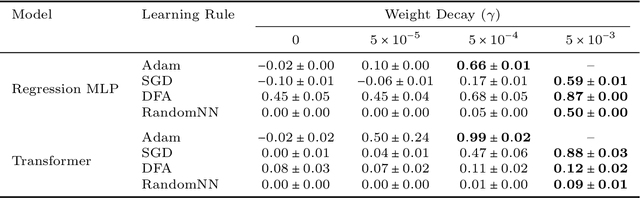
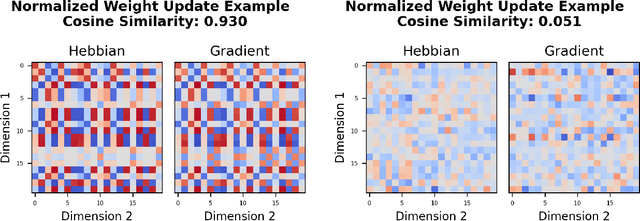
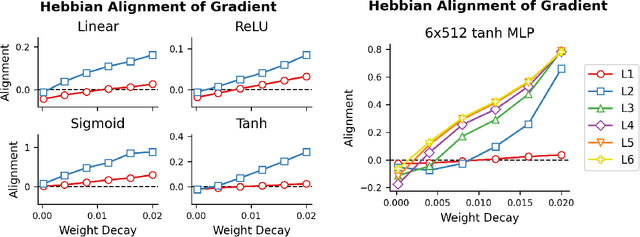
Stochastic Gradient Descent (SGD) has emerged as a remarkably effective learning algorithm, underpinning nearly all state-of-the-art machine learning models, from large language models to autonomous vehicles. Despite its practical success, SGD appears fundamentally distinct from biological learning mechanisms. It is widely believed that the biological brain can not implement gradient descent because it is nonlocal, and we have found little (if any) experimental evidence for it. In contrast, the brain is widely thought to learn via local Hebbian learning principles, which have been seen as incompatible with gradient descent. In this paper, we establish a theoretical and empirical connection between the learning signals of neural networks trained using SGD with weight decay and those trained with Hebbian learning near convergence. We show that SGD with regularization can appear to learn according to a Hebbian rule, and SGD with injected noise according to an anti-Hebbian rule. We also provide empirical evidence that Hebbian learning properties can emerge in a network with weight decay from virtually any learning rule--even random ones. These results may bridge a long-standing gap between artificial and biological learning, revealing Hebbian properties as an epiphenomenon of deeper optimization principles and cautioning against interpreting their presence in neural data as evidence against more complex hetero-synaptic mechanisms.

Neural Thermodynamics I: Entropic Forces in Deep and Universal Representation Learning

With the rapid discovery of emergent phenomena in deep learning and large language models, explaining and understanding their cause has become an urgent need. Here, we propose a rigorous entropic-force theory for understanding the learning dynamics of neural networks trained with stochastic gradient descent (SGD) and its variants. Building on the theory of parameter symmetries and an entropic loss landscape, we show that representation learning is crucially governed by emergent entropic forces arising from stochasticity and discrete-time updates. These forces systematically break continuous parameter symmetries and preserve discrete ones, leading to a series of gradient balance phenomena that resemble the equipartition property of thermal systems. These phenomena, in turn, (a) explain the universal alignment of neural representations between AI models and lead to a proof of the Platonic Representation Hypothesis, and (b) reconcile the seemingly contradictory observations of sharpness- and flatness-seeking behavior of deep learning optimization. Our theory and experiments demonstrate that a combination of entropic forces and symmetry breaking is key to understanding emergent phenomena in deep learning.

Heterosynaptic Circuits Are Universal Gradient Machines

We propose a design principle for the learning circuits of the biological brain. The principle states that almost any dendritic weights updated via heterosynaptic plasticity can implement a generalized and efficient class of gradient-based meta-learning. The theory suggests that a broad class of biologically plausible learning algorithms, together with the standard machine learning optimizers, can be grounded in heterosynaptic circuit motifs. This principle suggests that the phenomenology of (anti-) Hebbian (HBP) and heterosynaptic plasticity (HSP) may emerge from the same underlying dynamics, thus providing a unifying explanation. It also suggests an alternative perspective of neuroplasticity, where HSP is promoted to the primary learning and memory mechanism, and HBP is an emergent byproduct. We present simulations that show that (a) HSP can explain the metaplasticity of neurons, (b) HSP can explain the flexibility of the biology circuits, and (c) gradient learning can arise quickly from simple evolutionary dynamics that do not compute any explicit gradient. While our primary focus is on biology, the principle also implies a new approach to designing AI training algorithms and physically learnable AI hardware. Conceptually, our result demonstrates that contrary to the common belief, gradient computation may be extremely easy and common in nature.

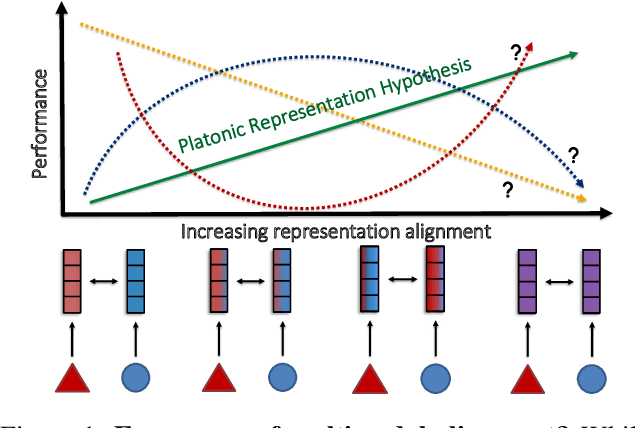
Understanding the Emergence of Multimodal Representation Alignment

Multimodal representation learning is fundamentally about transforming incomparable modalities into comparable representations. While prior research primarily focused on explicitly aligning these representations through targeted learning objectives and model architectures, a recent line of work has found that independently trained unimodal models of increasing scale and performance can become implicitly aligned with each other. These findings raise fundamental questions regarding the emergence of aligned representations in multimodal learning. Specifically: (1) when and why does alignment emerge implicitly? and (2) is alignment a reliable indicator of performance? Through a comprehensive empirical investigation, we demonstrate that both the emergence of alignment and its relationship with task performance depend on several critical data characteristics. These include, but are not necessarily limited to, the degree of similarity between the modalities and the balance between redundant and unique information they provide for the task. Our findings suggest that alignment may not be universally beneficial; rather, its impact on performance varies depending on the dataset and task. These insights can help practitioners determine whether increasing alignment between modalities is advantageous or, in some cases, detrimental to achieving optimal performance. Code is released at https://github.com/MeganTj/multimodal_alignment.

Parameter Symmetry Breaking and Restoration Determines the Hierarchical Learning in AI Systems

The dynamics of learning in modern large AI systems is hierarchical, often characterized by abrupt, qualitative shifts akin to phase transitions observed in physical systems. While these phenomena hold promise for uncovering the mechanisms behind neural networks and language models, existing theories remain fragmented, addressing specific cases. In this paper, we posit that parameter symmetry breaking and restoration serve as a unifying mechanism underlying these behaviors. We synthesize prior observations and show how this mechanism explains three distinct hierarchies in neural networks: learning dynamics, model complexity, and representation formation. By connecting these hierarchies, we highlight symmetry -- a cornerstone of theoretical physics -- as a potential fundamental principle in modern AI.