Compositional Generalization Requires More Than Disentangled Representations

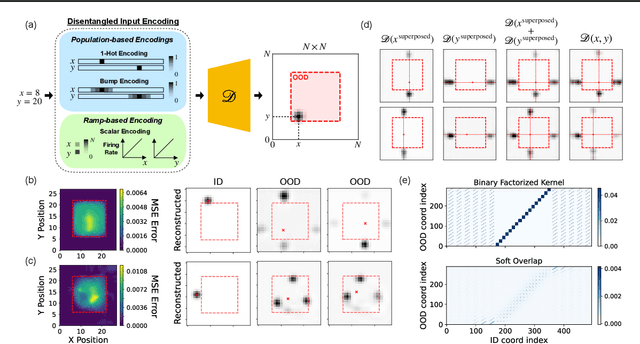
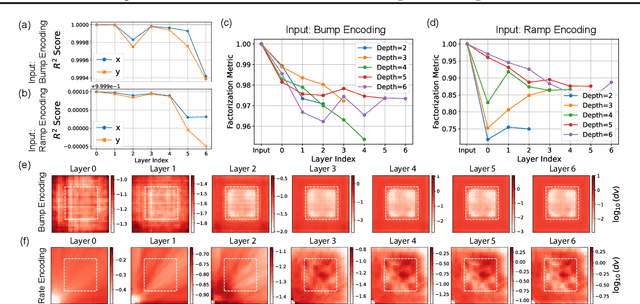
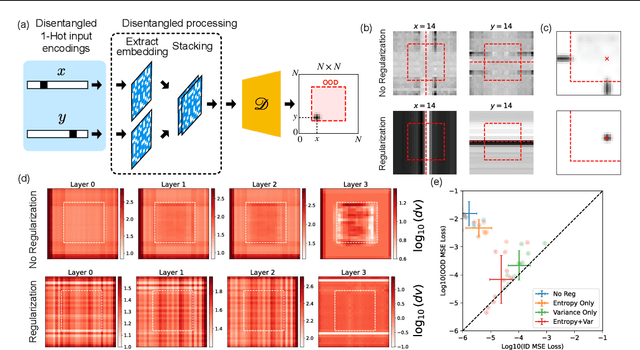
Composition-the ability to generate myriad variations from finite means-is believed to underlie powerful generalization. However, compositional generalization remains a key challenge for deep learning. A widely held assumption is that learning disentangled (factorized) representations naturally supports this kind of extrapolation. Yet, empirical results are mixed, with many generative models failing to recognize and compose factors to generate out-of-distribution (OOD) samples. In this work, we investigate a controlled 2D Gaussian "bump" generation task, demonstrating that standard generative architectures fail in OOD regions when training with partial data, even when supplied with fully disentangled $(x, y)$ coordinates, re-entangling them through subsequent layers. By examining the model's learned kernels and manifold geometry, we show that this failure reflects a "memorization" strategy for generation through the superposition of training data rather than by combining the true factorized features. We show that models forced-through architectural modifications with regularization or curated training data-to create disentangled representations in the full-dimensional representational (pixel) space can be highly data-efficient and effective at learning to compose in OOD regions. These findings underscore that bottlenecks with factorized/disentangled representations in an abstract representation are insufficient: the model must actively maintain or induce factorization directly in the representational space in order to achieve robust compositional generalization.

How Diffusion Models Learn to Factorize and Compose

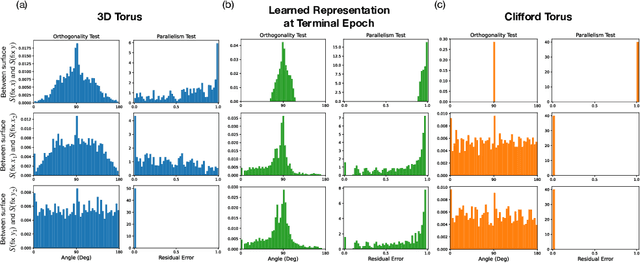
Diffusion models are capable of generating photo-realistic images that combine elements which likely do not appear together in the training set, demonstrating the ability to compositionally generalize. Nonetheless, the precise mechanism of compositionality and how it is acquired through training remains elusive. Inspired by cognitive neuroscientific approaches, we consider a highly reduced setting to examine whether and when diffusion models learn semantically meaningful and factorized representations of composable features. We performed extensive controlled experiments on conditional Denoising Diffusion Probabilistic Models (DDPMs) trained to generate various forms of 2D Gaussian data. We found that the models learn factorized but not fully continuous manifold representations for encoding continuous features of variation underlying the data. With such representations, models demonstrate superior feature compositionality but limited ability to interpolate over unseen values of a given feature. Our experimental results further demonstrate that diffusion models can attain compositionality with few compositional examples, suggesting a more efficient way to train DDPMs. Finally, we connect manifold formation in diffusion models to percolation theory in physics, offering insight into the sudden onset of factorized representation learning. Our thorough toy experiments thus contribute a deeper understanding of how diffusion models capture compositional structure in data.

Do Diffusion Models Learn Semantically Meaningful and Efficient Representations?

Diffusion models are capable of impressive feats of image generation with uncommon juxtapositions such as astronauts riding horses on the moon with properly placed shadows. These outputs indicate the ability to perform compositional generalization, but how do the models do so? We perform controlled experiments on conditional DDPMs learning to generate 2D spherical Gaussian bumps centered at specified $x$- and $y$-positions. Our results show that the emergence of semantically meaningful latent representations is key to achieving high performance. En route to successful performance over learning, the model traverses three distinct phases of latent representations: (phase A) no latent structure, (phase B) a 2D manifold of disordered states, and (phase C) a 2D ordered manifold. Corresponding to each of these phases, we identify qualitatively different generation behaviors: 1) multiple bumps are generated, 2) one bump is generated but at inaccurate $x$ and $y$ locations, 3) a bump is generated at the correct $x$ and y location. Furthermore, we show that even under imbalanced datasets where features ($x$- versus $y$-positions) are represented with skewed frequencies, the learning process for $x$ and $y$ is coupled rather than factorized, demonstrating that simple vanilla-flavored diffusion models cannot learn efficient representations in which localization in $x$ and $y$ are factorized into separate 1D tasks. These findings suggest the need for future work to find inductive biases that will push generative models to discover and exploit factorizable independent structures in their inputs, which will be required to vault these models into more data-efficient regimes.