The Blessing of Dimensionality in LLM Fine-tuning: A Variance-Curvature Perspective

Weight-perturbation evolution strategies (ES) can fine-tune billion-parameter language models with surprisingly small populations (e.g., $N\!\approx\!30$), contradicting classical zeroth-order curse-of-dimensionality intuition. We also observe a second seemingly separate phenomenon: under fixed hyperparameters, the stochastic fine-tuning reward often rises, peaks, and then degrades in both ES and GRPO. We argue that both effects reflect a shared geometric property of fine-tuning landscapes: they are low-dimensional in curvature. A small set of high-curvature dimensions dominates improvement, producing (i) heterogeneous time scales that yield rise-then-decay under fixed stochasticity, as captured by a minimal quadratic stochastic-ascent model, and (ii) degenerate improving updates, where many random perturbations share similar components along these directions. Using ES as a geometric probe on fine-tuning reward landscapes of GSM8K, ARC-C, and WinoGrande across Qwen2.5-Instruct models (0.5B--7B), we show that reward-improving perturbations remain empirically accessible with small populations across scales. Together, these results reconcile ES scalability with non-monotonic training dynamics and suggest that high-dimensional fine-tuning may admit a broader class of viable optimization methods than worst-case theory implies.

InputDSA: Demixing then Comparing Recurrent and Externally Driven Dynamics

In control problems and basic scientific modeling, it is important to compare observations with dynamical simulations. For example, comparing two neural systems can shed light on the nature of emergent computations in the brain and deep neural networks. Recently, Ostrow et al. (2023) introduced Dynamical Similarity Analysis (DSA), a method to measure the similarity of two systems based on their recurrent dynamics rather than geometry or topology. However, DSA does not consider how inputs affect the dynamics, meaning that two similar systems, if driven differently, may be classified as different. Because real-world dynamical systems are rarely autonomous, it is important to account for the effects of input drive. To this end, we introduce a novel metric for comparing both intrinsic (recurrent) and input-driven dynamics, called InputDSA (iDSA). InputDSA extends the DSA framework by estimating and comparing both input and intrinsic dynamic operators using a variant of Dynamic Mode Decomposition with control (DMDc) based on subspace identification. We demonstrate that InputDSA can successfully compare partially observed, input-driven systems from noisy data. We show that when the true inputs are unknown, surrogate inputs can be substituted without a major deterioration in similarity estimates. We apply InputDSA on Recurrent Neural Networks (RNNs) trained with Deep Reinforcement Learning, identifying that high-performing networks are dynamically similar to one another, while low-performing networks are more diverse. Lastly, we apply InputDSA to neural data recorded from rats performing a cognitive task, demonstrating that it identifies a transition from input-driven evidence accumulation to intrinsically-driven decision-making. Our work demonstrates that InputDSA is a robust and efficient method for comparing intrinsic dynamics and the effect of external input on dynamical systems.

Compositional Generalization Requires More Than Disentangled Representations

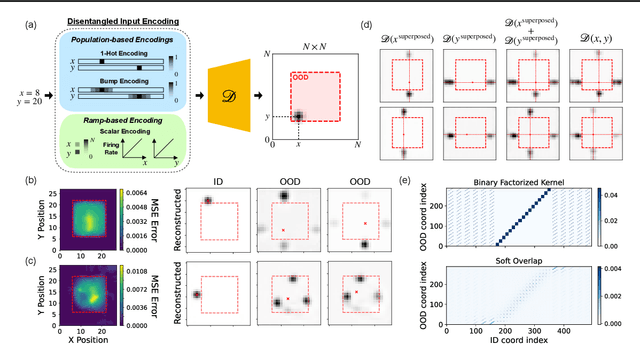
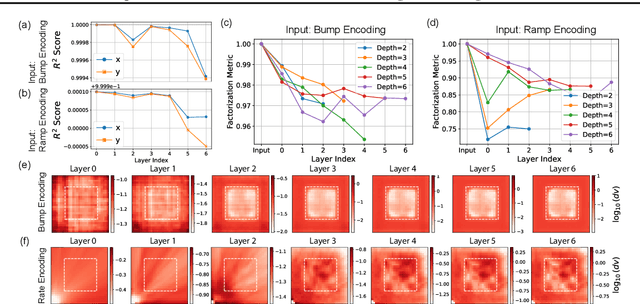
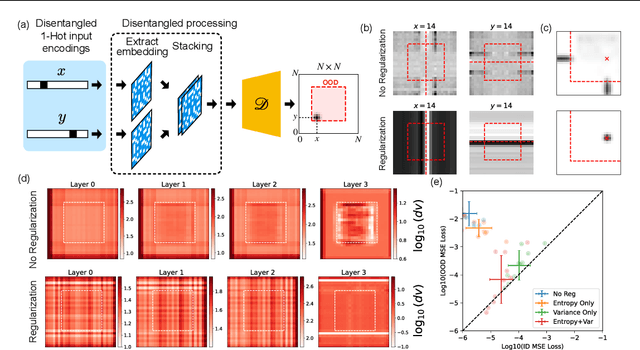
Composition-the ability to generate myriad variations from finite means-is believed to underlie powerful generalization. However, compositional generalization remains a key challenge for deep learning. A widely held assumption is that learning disentangled (factorized) representations naturally supports this kind of extrapolation. Yet, empirical results are mixed, with many generative models failing to recognize and compose factors to generate out-of-distribution (OOD) samples. In this work, we investigate a controlled 2D Gaussian "bump" generation task, demonstrating that standard generative architectures fail in OOD regions when training with partial data, even when supplied with fully disentangled $(x, y)$ coordinates, re-entangling them through subsequent layers. By examining the model's learned kernels and manifold geometry, we show that this failure reflects a "memorization" strategy for generation through the superposition of training data rather than by combining the true factorized features. We show that models forced-through architectural modifications with regularization or curated training data-to create disentangled representations in the full-dimensional representational (pixel) space can be highly data-efficient and effective at learning to compose in OOD regions. These findings underscore that bottlenecks with factorized/disentangled representations in an abstract representation are insufficient: the model must actively maintain or induce factorization directly in the representational space in order to achieve robust compositional generalization.

Key-value memory in the brain

Classical models of memory in psychology and neuroscience rely on similarity-based retrieval of stored patterns, where similarity is a function of retrieval cues and the stored patterns. While parsimonious, these models do not allow distinct representations for storage and retrieval, despite their distinct computational demands. Key-value memory systems, in contrast, distinguish representations used for storage (values) and those used for retrieval (keys). This allows key-value memory systems to optimize simultaneously for fidelity in storage and discriminability in retrieval. We review the computational foundations of key-value memory, its role in modern machine learning systems, related ideas from psychology and neuroscience, applications to a number of empirical puzzles, and possible biological implementations.

Permutation Invariant Learning with High-Dimensional Particle Filters

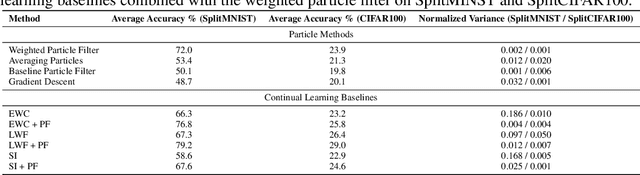
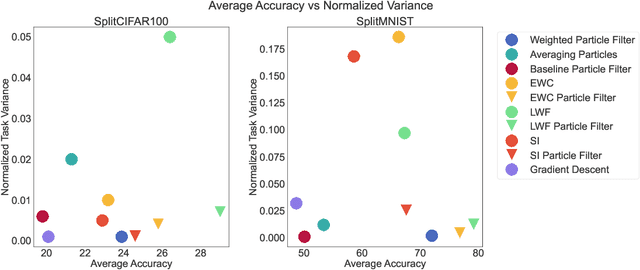
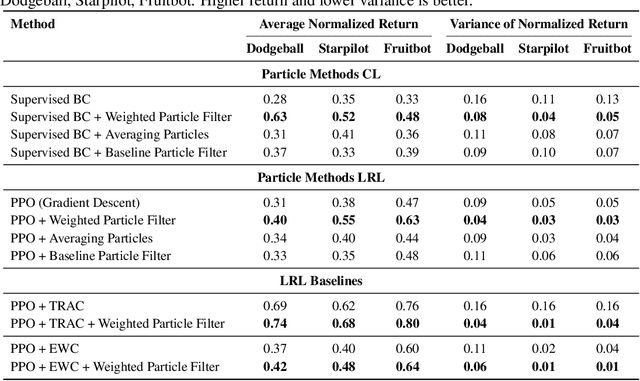
Sequential learning in deep models often suffers from challenges such as catastrophic forgetting and loss of plasticity, largely due to the permutation dependence of gradient-based algorithms, where the order of training data impacts the learning outcome. In this work, we introduce a novel permutation-invariant learning framework based on high-dimensional particle filters. We theoretically demonstrate that particle filters are invariant to the sequential ordering of training minibatches or tasks, offering a principled solution to mitigate catastrophic forgetting and loss-of-plasticity. We develop an efficient particle filter for optimizing high-dimensional models, combining the strengths of Bayesian methods with gradient-based optimization. Through extensive experiments on continual supervised and reinforcement learning benchmarks, including SplitMNIST, SplitCIFAR100, and ProcGen, we empirically show that our method consistently improves performance, while reducing variance compared to standard baselines.

ImageNet-RIB Benchmark: Large Pre-Training Datasets Don't Guarantee Robustness after Fine-Tuning

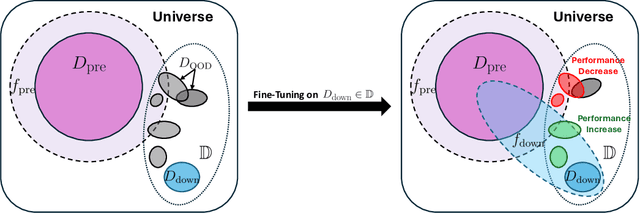
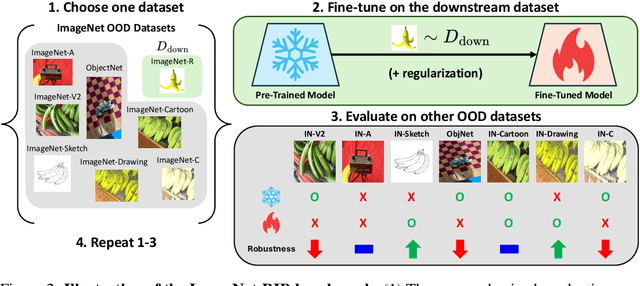
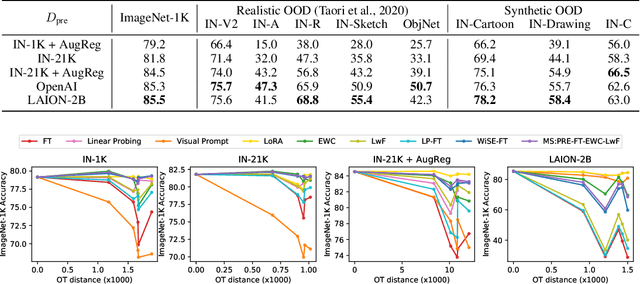
Highly performant large-scale pre-trained models promise to also provide a valuable foundation for learning specialized tasks, by fine-tuning the model to the desired task. By starting from a good general-purpose model, the goal is to achieve both specialization in the target task and maintain robustness. To assess the robustness of models to out-of-distribution samples after fine-tuning on downstream datasets, we introduce a new robust fine-tuning benchmark, ImageNet-RIB (Robustness Inheritance Benchmark). The benchmark consists of a set of related but distinct specialized (downstream) tasks; pre-trained models are fine-tuned on one task in the set and their robustness is assessed on the rest, iterating across all tasks for fine-tuning and assessment. We find that the continual learning methods, EWC and LwF maintain robustness after fine-tuning though fine-tuning generally does reduce performance on generalization to related downstream tasks across models. Not surprisingly, models pre-trained on large and rich datasets exhibit higher initial robustness across datasets and suffer more pronounced degradation during fine-tuning. The distance between the pre-training and downstream datasets, measured by optimal transport, predicts this performance degradation on the pre-training dataset. However, counterintuitively, model robustness after fine-tuning on related downstream tasks is the worst when the pre-training dataset is the richest and the most diverse. This suggests that starting with the strongest foundation model is not necessarily the best approach for performance on specialist tasks. The benchmark thus offers key insights for developing more resilient fine-tuning strategies and building robust machine learning models. https://jd730.github.io/projects/ImageNet-RIB

Breaking Neural Network Scaling Laws with Modularity

Modular neural networks outperform nonmodular neural networks on tasks ranging from visual question answering to robotics. These performance improvements are thought to be due to modular networks' superior ability to model the compositional and combinatorial structure of real-world problems. However, a theoretical explanation of how modularity improves generalizability, and how to leverage task modularity while training networks remains elusive. Using recent theoretical progress in explaining neural network generalization, we investigate how the amount of training data required to generalize on a task varies with the intrinsic dimensionality of a task's input. We show theoretically that when applied to modularly structured tasks, while nonmodular networks require an exponential number of samples with task dimensionality, modular networks' sample complexity is independent of task dimensionality: modular networks can generalize in high dimensions. We then develop a novel learning rule for modular networks to exploit this advantage and empirically show the improved generalization of the rule, both in- and out-of-distribution, on high-dimensional, modular tasks.

Unified Neural Network Scaling Laws and Scale-time Equivalence

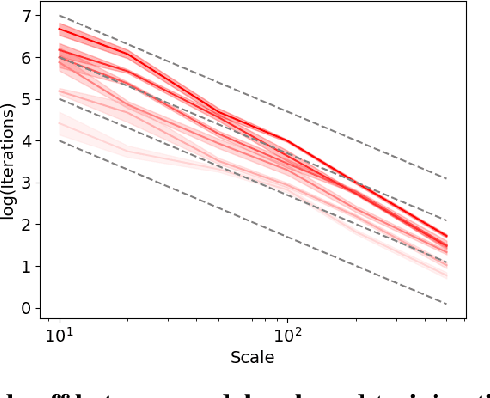
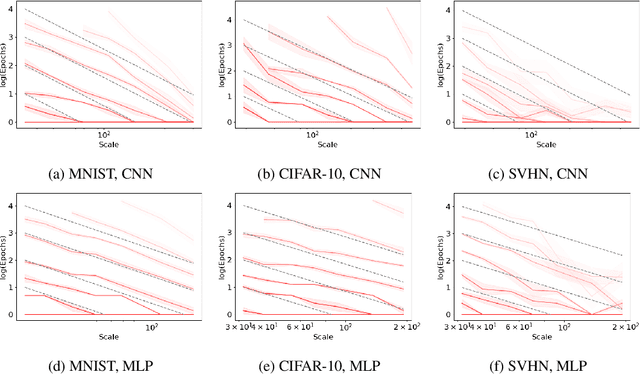
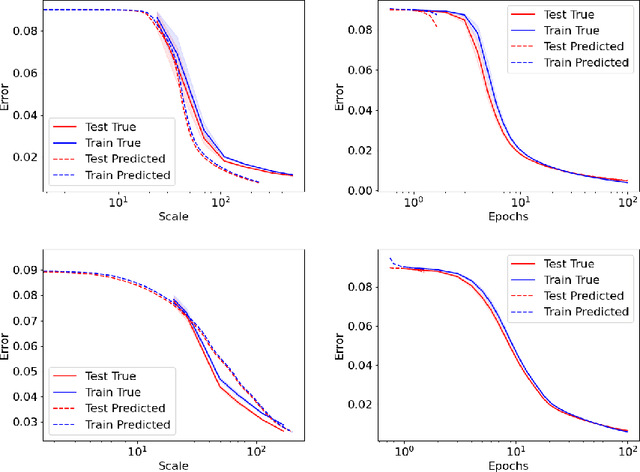
As neural networks continue to grow in size but datasets might not, it is vital to understand how much performance improvement can be expected: is it more important to scale network size or data volume? Thus, neural network scaling laws, which characterize how test error varies with network size and data volume, have become increasingly important. However, existing scaling laws are often applicable only in limited regimes and often do not incorporate or predict well-known phenomena such as double descent. Here, we present a novel theoretical characterization of how three factors -- model size, training time, and data volume -- interact to determine the performance of deep neural networks. We first establish a theoretical and empirical equivalence between scaling the size of a neural network and increasing its training time proportionally. Scale-time equivalence challenges the current practice, wherein large models are trained for small durations, and suggests that smaller models trained over extended periods could match their efficacy. It also leads to a novel method for predicting the performance of large-scale networks from small-scale networks trained for extended epochs, and vice versa. We next combine scale-time equivalence with a linear model analysis of double descent to obtain a unified theoretical scaling law, which we confirm with experiments across vision benchmarks and network architectures. These laws explain several previously unexplained phenomena: reduced data requirements for generalization in larger models, heightened sensitivity to label noise in overparameterized models, and instances where increasing model scale does not necessarily enhance performance. Our findings hold significant implications for the practical deployment of neural networks, offering a more accessible and efficient path to training and fine-tuning large models.

How Diffusion Models Learn to Factorize and Compose

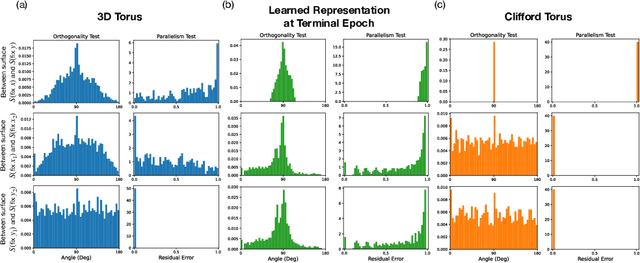
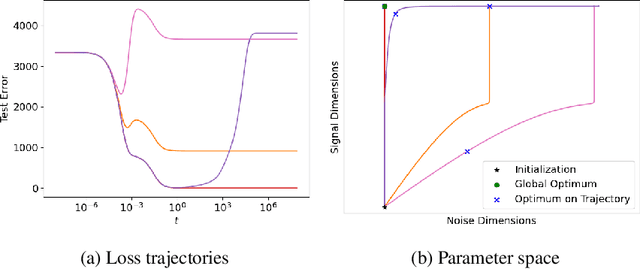
Diffusion models are capable of generating photo-realistic images that combine elements which likely do not appear together in the training set, demonstrating the ability to compositionally generalize. Nonetheless, the precise mechanism of compositionality and how it is acquired through training remains elusive. Inspired by cognitive neuroscientific approaches, we consider a highly reduced setting to examine whether and when diffusion models learn semantically meaningful and factorized representations of composable features. We performed extensive controlled experiments on conditional Denoising Diffusion Probabilistic Models (DDPMs) trained to generate various forms of 2D Gaussian data. We found that the models learn factorized but not fully continuous manifold representations for encoding continuous features of variation underlying the data. With such representations, models demonstrate superior feature compositionality but limited ability to interpolate over unseen values of a given feature. Our experimental results further demonstrate that diffusion models can attain compositionality with few compositional examples, suggesting a more efficient way to train DDPMs. Finally, we connect manifold formation in diffusion models to percolation theory in physics, offering insight into the sudden onset of factorized representation learning. Our thorough toy experiments thus contribute a deeper understanding of how diffusion models capture compositional structure in data.

Towards Exact Computation of Inductive Bias

Much research in machine learning involves finding appropriate inductive biases (e.g. convolutional neural networks, momentum-based optimizers, transformers) to promote generalization on tasks. However, quantification of the amount of inductive bias associated with these architectures and hyperparameters has been limited. We propose a novel method for efficiently computing the inductive bias required for generalization on a task with a fixed training data budget; formally, this corresponds to the amount of information required to specify well-generalizing models within a specific hypothesis space of models. Our approach involves modeling the loss distribution of random hypotheses drawn from a hypothesis space to estimate the required inductive bias for a task relative to these hypotheses. Unlike prior work, our method provides a direct estimate of inductive bias without using bounds and is applicable to diverse hypothesis spaces. Moreover, we derive approximation error bounds for our estimation approach in terms of the number of sampled hypotheses. Consistent with prior results, our empirical results demonstrate that higher dimensional tasks require greater inductive bias. We show that relative to other expressive model classes, neural networks as a model class encode large amounts of inductive bias. Furthermore, our measure quantifies the relative difference in inductive bias between different neural network architectures. Our proposed inductive bias metric provides an information-theoretic interpretation of the benefits of specific model architectures for certain tasks and provides a quantitative guide to developing tasks requiring greater inductive bias, thereby encouraging the development of more powerful inductive biases.