Unified Neural Network Scaling Laws and Scale-time Equivalence
Paper and Code
Sep 09, 2024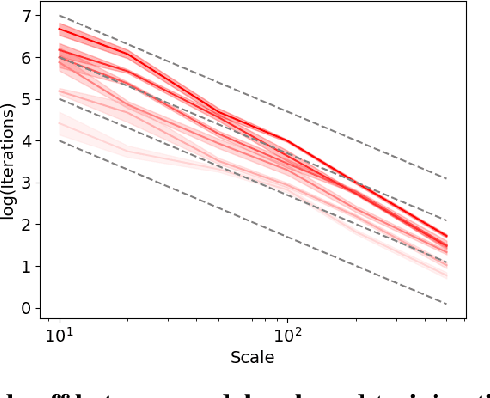
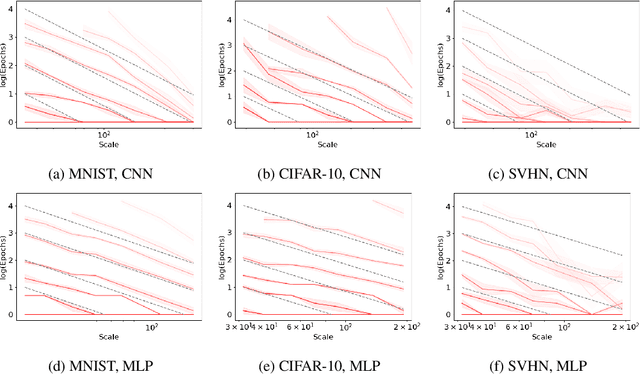
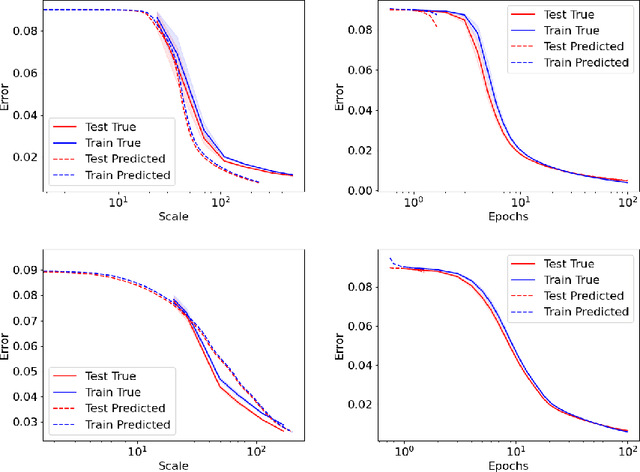
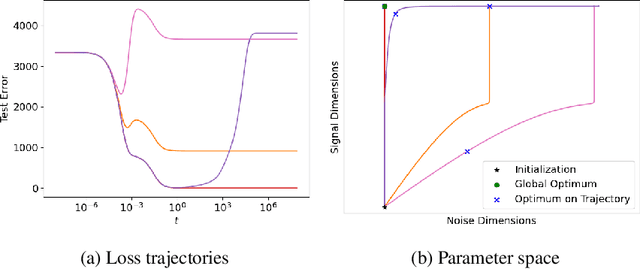
As neural networks continue to grow in size but datasets might not, it is vital to understand how much performance improvement can be expected: is it more important to scale network size or data volume? Thus, neural network scaling laws, which characterize how test error varies with network size and data volume, have become increasingly important. However, existing scaling laws are often applicable only in limited regimes and often do not incorporate or predict well-known phenomena such as double descent. Here, we present a novel theoretical characterization of how three factors -- model size, training time, and data volume -- interact to determine the performance of deep neural networks. We first establish a theoretical and empirical equivalence between scaling the size of a neural network and increasing its training time proportionally. Scale-time equivalence challenges the current practice, wherein large models are trained for small durations, and suggests that smaller models trained over extended periods could match their efficacy. It also leads to a novel method for predicting the performance of large-scale networks from small-scale networks trained for extended epochs, and vice versa. We next combine scale-time equivalence with a linear model analysis of double descent to obtain a unified theoretical scaling law, which we confirm with experiments across vision benchmarks and network architectures. These laws explain several previously unexplained phenomena: reduced data requirements for generalization in larger models, heightened sensitivity to label noise in overparameterized models, and instances where increasing model scale does not necessarily enhance performance. Our findings hold significant implications for the practical deployment of neural networks, offering a more accessible and efficient path to training and fine-tuning large models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge