Permutation Invariant Learning with High-Dimensional Particle Filters

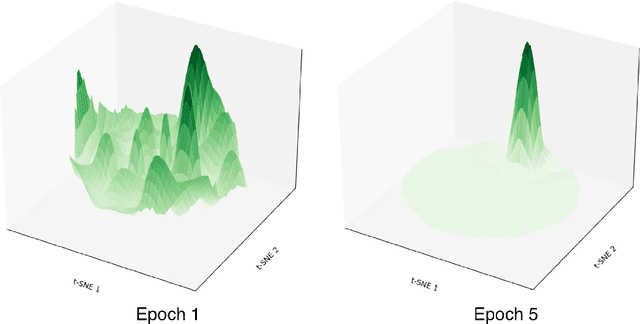
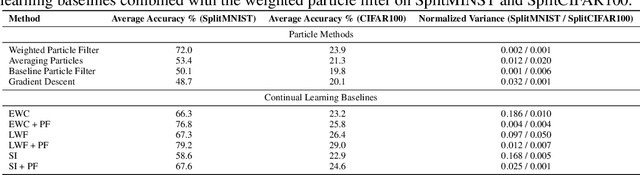
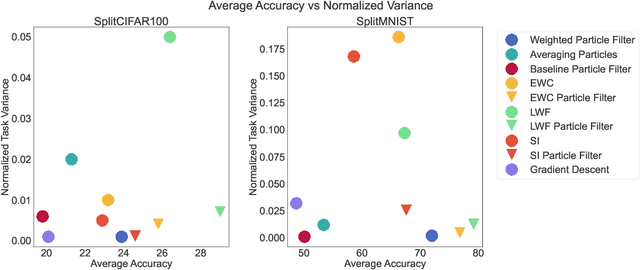
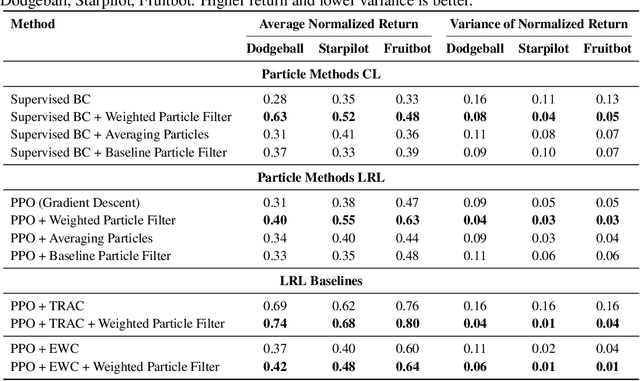
Sequential learning in deep models often suffers from challenges such as catastrophic forgetting and loss of plasticity, largely due to the permutation dependence of gradient-based algorithms, where the order of training data impacts the learning outcome. In this work, we introduce a novel permutation-invariant learning framework based on high-dimensional particle filters. We theoretically demonstrate that particle filters are invariant to the sequential ordering of training minibatches or tasks, offering a principled solution to mitigate catastrophic forgetting and loss-of-plasticity. We develop an efficient particle filter for optimizing high-dimensional models, combining the strengths of Bayesian methods with gradient-based optimization. Through extensive experiments on continual supervised and reinforcement learning benchmarks, including SplitMNIST, SplitCIFAR100, and ProcGen, we empirically show that our method consistently improves performance, while reducing variance compared to standard baselines.

ImageNet-RIB Benchmark: Large Pre-Training Datasets Don't Guarantee Robustness after Fine-Tuning

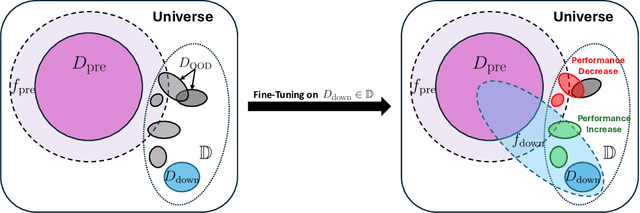
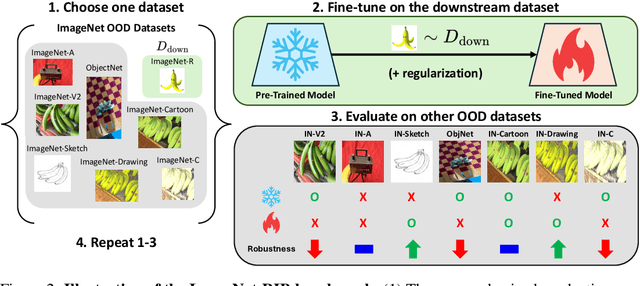
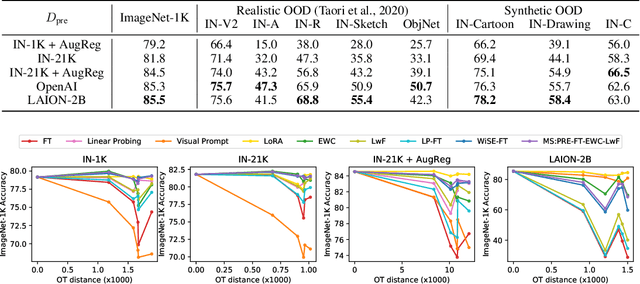
Highly performant large-scale pre-trained models promise to also provide a valuable foundation for learning specialized tasks, by fine-tuning the model to the desired task. By starting from a good general-purpose model, the goal is to achieve both specialization in the target task and maintain robustness. To assess the robustness of models to out-of-distribution samples after fine-tuning on downstream datasets, we introduce a new robust fine-tuning benchmark, ImageNet-RIB (Robustness Inheritance Benchmark). The benchmark consists of a set of related but distinct specialized (downstream) tasks; pre-trained models are fine-tuned on one task in the set and their robustness is assessed on the rest, iterating across all tasks for fine-tuning and assessment. We find that the continual learning methods, EWC and LwF maintain robustness after fine-tuning though fine-tuning generally does reduce performance on generalization to related downstream tasks across models. Not surprisingly, models pre-trained on large and rich datasets exhibit higher initial robustness across datasets and suffer more pronounced degradation during fine-tuning. The distance between the pre-training and downstream datasets, measured by optimal transport, predicts this performance degradation on the pre-training dataset. However, counterintuitively, model robustness after fine-tuning on related downstream tasks is the worst when the pre-training dataset is the richest and the most diverse. This suggests that starting with the strongest foundation model is not necessarily the best approach for performance on specialist tasks. The benchmark thus offers key insights for developing more resilient fine-tuning strategies and building robust machine learning models. https://jd730.github.io/projects/ImageNet-RIB

Breaking Neural Network Scaling Laws with Modularity

Modular neural networks outperform nonmodular neural networks on tasks ranging from visual question answering to robotics. These performance improvements are thought to be due to modular networks' superior ability to model the compositional and combinatorial structure of real-world problems. However, a theoretical explanation of how modularity improves generalizability, and how to leverage task modularity while training networks remains elusive. Using recent theoretical progress in explaining neural network generalization, we investigate how the amount of training data required to generalize on a task varies with the intrinsic dimensionality of a task's input. We show theoretically that when applied to modularly structured tasks, while nonmodular networks require an exponential number of samples with task dimensionality, modular networks' sample complexity is independent of task dimensionality: modular networks can generalize in high dimensions. We then develop a novel learning rule for modular networks to exploit this advantage and empirically show the improved generalization of the rule, both in- and out-of-distribution, on high-dimensional, modular tasks.

Unified Neural Network Scaling Laws and Scale-time Equivalence

As neural networks continue to grow in size but datasets might not, it is vital to understand how much performance improvement can be expected: is it more important to scale network size or data volume? Thus, neural network scaling laws, which characterize how test error varies with network size and data volume, have become increasingly important. However, existing scaling laws are often applicable only in limited regimes and often do not incorporate or predict well-known phenomena such as double descent. Here, we present a novel theoretical characterization of how three factors -- model size, training time, and data volume -- interact to determine the performance of deep neural networks. We first establish a theoretical and empirical equivalence between scaling the size of a neural network and increasing its training time proportionally. Scale-time equivalence challenges the current practice, wherein large models are trained for small durations, and suggests that smaller models trained over extended periods could match their efficacy. It also leads to a novel method for predicting the performance of large-scale networks from small-scale networks trained for extended epochs, and vice versa. We next combine scale-time equivalence with a linear model analysis of double descent to obtain a unified theoretical scaling law, which we confirm with experiments across vision benchmarks and network architectures. These laws explain several previously unexplained phenomena: reduced data requirements for generalization in larger models, heightened sensitivity to label noise in overparameterized models, and instances where increasing model scale does not necessarily enhance performance. Our findings hold significant implications for the practical deployment of neural networks, offering a more accessible and efficient path to training and fine-tuning large models.

Towards Exact Computation of Inductive Bias

Much research in machine learning involves finding appropriate inductive biases (e.g. convolutional neural networks, momentum-based optimizers, transformers) to promote generalization on tasks. However, quantification of the amount of inductive bias associated with these architectures and hyperparameters has been limited. We propose a novel method for efficiently computing the inductive bias required for generalization on a task with a fixed training data budget; formally, this corresponds to the amount of information required to specify well-generalizing models within a specific hypothesis space of models. Our approach involves modeling the loss distribution of random hypotheses drawn from a hypothesis space to estimate the required inductive bias for a task relative to these hypotheses. Unlike prior work, our method provides a direct estimate of inductive bias without using bounds and is applicable to diverse hypothesis spaces. Moreover, we derive approximation error bounds for our estimation approach in terms of the number of sampled hypotheses. Consistent with prior results, our empirical results demonstrate that higher dimensional tasks require greater inductive bias. We show that relative to other expressive model classes, neural networks as a model class encode large amounts of inductive bias. Furthermore, our measure quantifies the relative difference in inductive bias between different neural network architectures. Our proposed inductive bias metric provides an information-theoretic interpretation of the benefits of specific model architectures for certain tasks and provides a quantitative guide to developing tasks requiring greater inductive bias, thereby encouraging the development of more powerful inductive biases.

Resampling-free Particle Filters in High-dimensions

State estimation is crucial for the performance and safety of numerous robotic applications. Among the suite of estimation techniques, particle filters have been identified as a powerful solution due to their non-parametric nature. Yet, in high-dimensional state spaces, these filters face challenges such as 'particle deprivation' which hinders accurate representation of the true posterior distribution. This paper introduces a novel resampling-free particle filter designed to mitigate particle deprivation by forgoing the traditional resampling step. This ensures a broader and more diverse particle set, especially vital in high-dimensional scenarios. Theoretically, our proposed filter is shown to offer a near-accurate representation of the desired posterior distribution in high-dimensional contexts. Empirically, the effectiveness of our approach is underscored through a high-dimensional synthetic state estimation task and a 6D pose estimation derived from videos. We posit that as robotic systems evolve with greater degrees of freedom, particle filters tailored for high-dimensional state spaces will be indispensable.

Neuro-Inspired Fragmentation and Recall to Overcome Catastrophic Forgetting in Curiosity

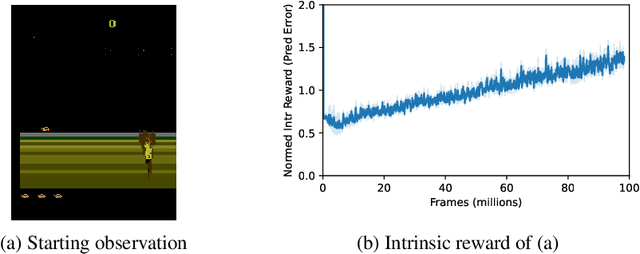
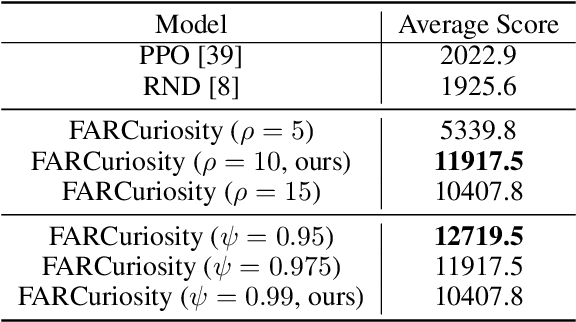
Deep reinforcement learning methods exhibit impressive performance on a range of tasks but still struggle on hard exploration tasks in large environments with sparse rewards. To address this, intrinsic rewards can be generated using forward model prediction errors that decrease as the environment becomes known, and incentivize an agent to explore novel states. While prediction-based intrinsic rewards can help agents solve hard exploration tasks, they can suffer from catastrophic forgetting and actually increase at visited states. We first examine the conditions and causes of catastrophic forgetting in grid world environments. We then propose a new method FARCuriosity, inspired by how humans and animals learn. The method depends on fragmentation and recall: an agent fragments an environment based on surprisal, and uses different local curiosity modules (prediction-based intrinsic reward functions) for each fragment so that modules are not trained on the entire environment. At each fragmentation event, the agent stores the current module in long-term memory (LTM) and either initializes a new module or recalls a previously stored module based on its match with the current state. With fragmentation and recall, FARCuriosity achieves less forgetting and better overall performance in games with varied and heterogeneous environments in the Atari benchmark suite of tasks. Thus, this work highlights the problem of catastrophic forgetting in prediction-based curiosity methods and proposes a solution.

Neuro-Inspired Efficient Map Building via Fragmentation and Recall

Animals and robots navigate through environments by building and refining maps of the space. These maps enable functions including navigating back to home, planning, search, and foraging. In large environments, exploration of the space is a hard problem: agents can become stuck in local regions. Here, we use insights from neuroscience to propose and apply the concept of Fragmentation-and-Recall (FarMap), with agents solving the mapping problem by building local maps via a surprisal-based clustering of space, which they use to set subgoals for spatial exploration. Agents build and use a local map to predict their observations; high surprisal leads to a ``fragmentation event'' that truncates the local map. At these events, the recent local map is placed into long-term memory (LTM), and a different local map is initialized. If observations at a fracture point match observations in one of the stored local maps, that map is recalled (and thus reused) from LTM. The fragmentation points induce a natural online clustering of the larger space, forming a set of intrinsic potential subgoals that are stored in LTM as a topological graph. Agents choose their next subgoal from the set of near and far potential subgoals from within the current local map or LTM, respectively. Thus, local maps guide exploration locally, while LTM promotes global exploration. We evaluate FarMap on complex procedurally-generated spatial environments to demonstrate that this mapping strategy much more rapidly covers the environment (number of agent steps and wall clock time) and is more efficient in active memory usage, without loss of performance.

Model-agnostic Measure of Generalization Difficulty

The measure of a machine learning algorithm is the difficulty of the tasks it can perform, and sufficiently difficult tasks are critical drivers of strong machine learning models. However, quantifying the generalization difficulty of machine learning benchmarks has remained challenging. We propose what is to our knowledge the first model-agnostic measure of the inherent generalization difficulty of tasks. Our inductive bias complexity measure quantifies the total information required to generalize well on a task minus the information provided by the data. It does so by measuring the fractional volume occupied by hypotheses that generalize on a task given that they fit the training data. It scales exponentially with the intrinsic dimensionality of the space over which the model must generalize but only polynomially in resolution per dimension, showing that tasks which require generalizing over many dimensions are drastically more difficult than tasks involving more detail in fewer dimensions. Our measure can be applied to compute and compare supervised learning, reinforcement learning and meta-learning generalization difficulties against each other. We show that applied empirically, it formally quantifies intuitively expected trends, e.g. that in terms of required inductive bias, MNIST < CIFAR10 < Imagenet and fully observable Markov decision processes (MDPs) < partially observable MDPs. Further, we show that classification of complex images $<$ few-shot meta-learning with simple images. Our measure provides a quantitative metric to guide the construction of more complex tasks requiring greater inductive bias, and thereby encourages the development of more sophisticated architectures and learning algorithms with more powerful generalization capabilities.

Double Descent Demystified: Identifying, Interpreting & Ablating the Sources of a Deep Learning Puzzle

Double descent is a surprising phenomenon in machine learning, in which as the number of model parameters grows relative to the number of data, test error drops as models grow ever larger into the highly overparameterized (data undersampled) regime. This drop in test error flies against classical learning theory on overfitting and has arguably underpinned the success of large models in machine learning. This non-monotonic behavior of test loss depends on the number of data, the dimensionality of the data and the number of model parameters. Here, we briefly describe double descent, then provide an explanation of why double descent occurs in an informal and approachable manner, requiring only familiarity with linear algebra and introductory probability. We provide visual intuition using polynomial regression, then mathematically analyze double descent with ordinary linear regression and identify three interpretable factors that, when simultaneously all present, together create double descent. We demonstrate that double descent occurs on real data when using ordinary linear regression, then demonstrate that double descent does not occur when any of the three factors are ablated. We use this understanding to shed light on recent observations in nonlinear models concerning superposition and double descent. Code is publicly available.