Double Descent Demystified: Identifying, Interpreting & Ablating the Sources of a Deep Learning Puzzle

Double descent is a surprising phenomenon in machine learning, in which as the number of model parameters grows relative to the number of data, test error drops as models grow ever larger into the highly overparameterized (data undersampled) regime. This drop in test error flies against classical learning theory on overfitting and has arguably underpinned the success of large models in machine learning. This non-monotonic behavior of test loss depends on the number of data, the dimensionality of the data and the number of model parameters. Here, we briefly describe double descent, then provide an explanation of why double descent occurs in an informal and approachable manner, requiring only familiarity with linear algebra and introductory probability. We provide visual intuition using polynomial regression, then mathematically analyze double descent with ordinary linear regression and identify three interpretable factors that, when simultaneously all present, together create double descent. We demonstrate that double descent occurs on real data when using ordinary linear regression, then demonstrate that double descent does not occur when any of the three factors are ablated. We use this understanding to shed light on recent observations in nonlinear models concerning superposition and double descent. Code is publicly available.

Bias-variance decomposition of overparameterized regression with random linear features

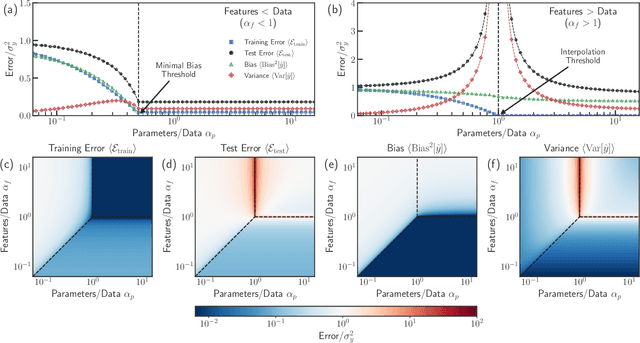
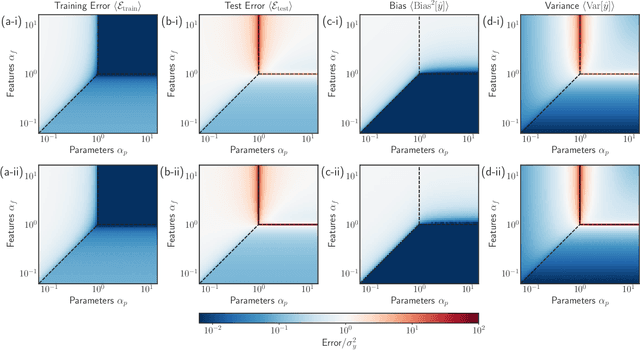
In classical statistics, the bias-variance trade-off describes how varying a model's complexity (e.g., number of fit parameters) affects its ability to make accurate predictions. According to this trade-off, optimal performance is achieved when a model is expressive enough to capture trends in the data, yet not so complex that it overfits idiosyncratic features of the training data. Recently, it has become clear that this classic understanding of the bias-variance must be fundamentally revisited in light of the incredible predictive performance of "overparameterized models" -- models that avoid overfitting even when the number of fit parameters is large enough to perfectly fit the training data. Here, we present results for one of the simplest examples of an overparameterized model: regression with random linear features (i.e. a two-layer neural network with a linear activation function). Using the zero-temperature cavity method, we derive analytic expressions for the training error, test error, bias, and variance. We show that the linear random features model exhibits three phase transitions: two different transitions to an interpolation regime where the training error is zero, along with an additional transition between regimes with large bias and minimal bias. Using random matrix theory, we show how each transition arises due to small nonzero eigenvalues in the Hessian matrix. Finally, we compare and contrast the phase diagram of the random linear features model to the random nonlinear features model and ordinary regression, highlighting the new phase transitions that result from the use of linear basis functions.

The Geometry of Over-parameterized Regression and Adversarial Perturbations

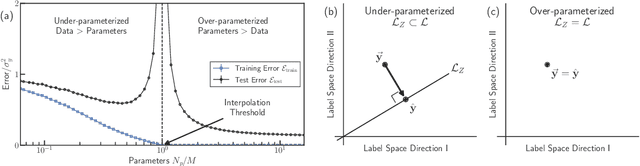
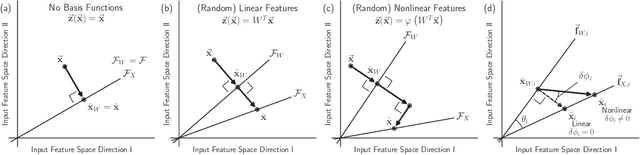
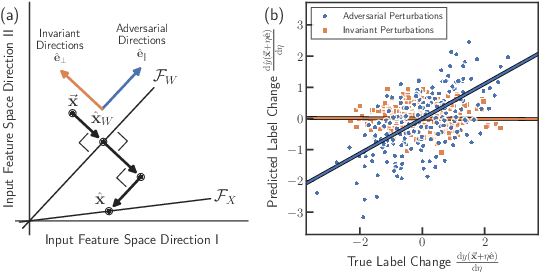
Classical regression has a simple geometric description in terms of a projection of the training labels onto the column space of the design matrix. However, for over-parameterized models -- where the number of fit parameters is large enough to perfectly fit the training data -- this picture becomes uninformative. Here, we present an alternative geometric interpretation of regression that applies to both under- and over-parameterized models. Unlike the classical picture which takes place in the space of training labels, our new picture resides in the space of input features. This new feature-based perspective provides a natural geometric interpretation of the double-descent phenomenon in the context of bias and variance, explaining why it can occur even in the absence of label noise. Furthermore, we show that adversarial perturbations -- small perturbations to the input features that result in large changes in label values -- are a generic feature of biased models, arising from the underlying geometry. We demonstrate these ideas by analyzing three minimal models for over-parameterized linear least squares regression: without basis functions (input features equal model features) and with linear or nonlinear basis functions (two-layer neural networks with linear or nonlinear activation functions, respectively).

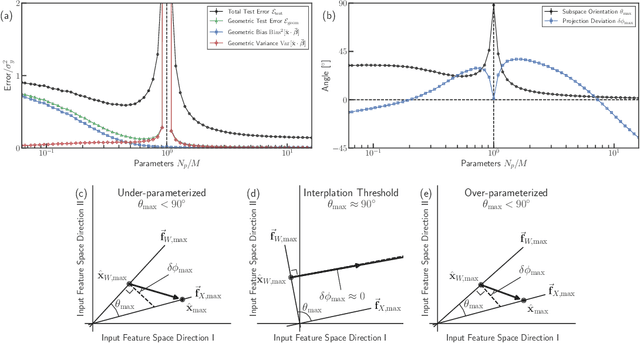
Memorizing without overfitting: Bias, variance, and interpolation in over-parameterized models

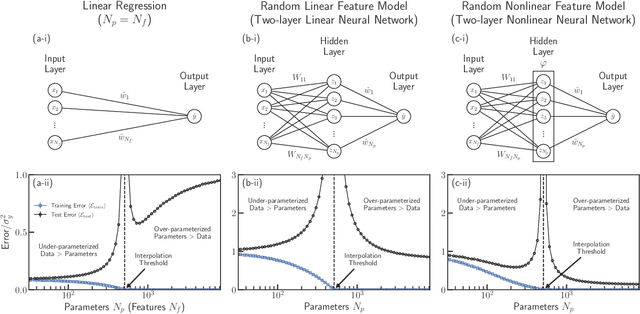
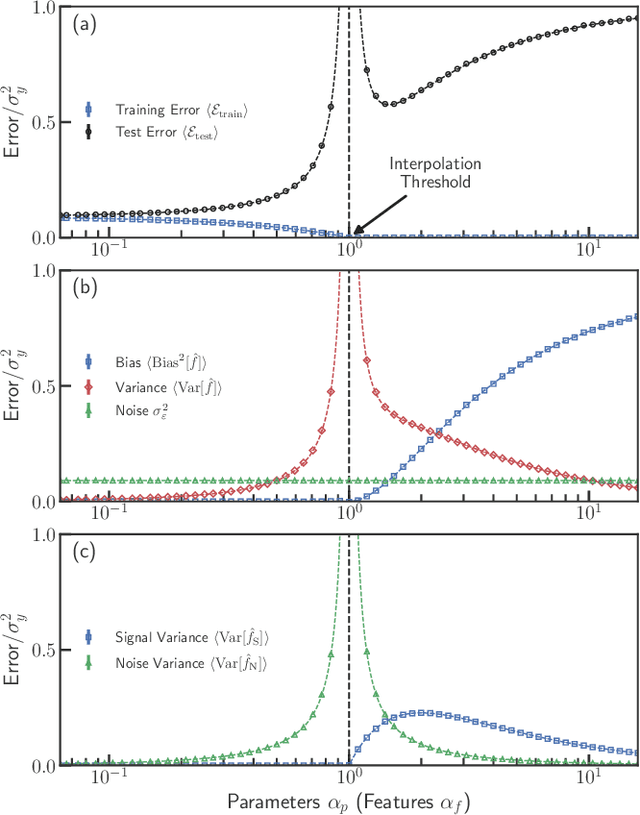
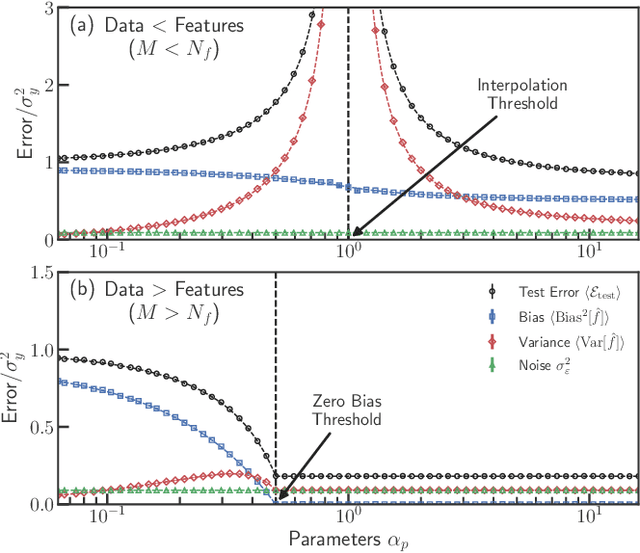
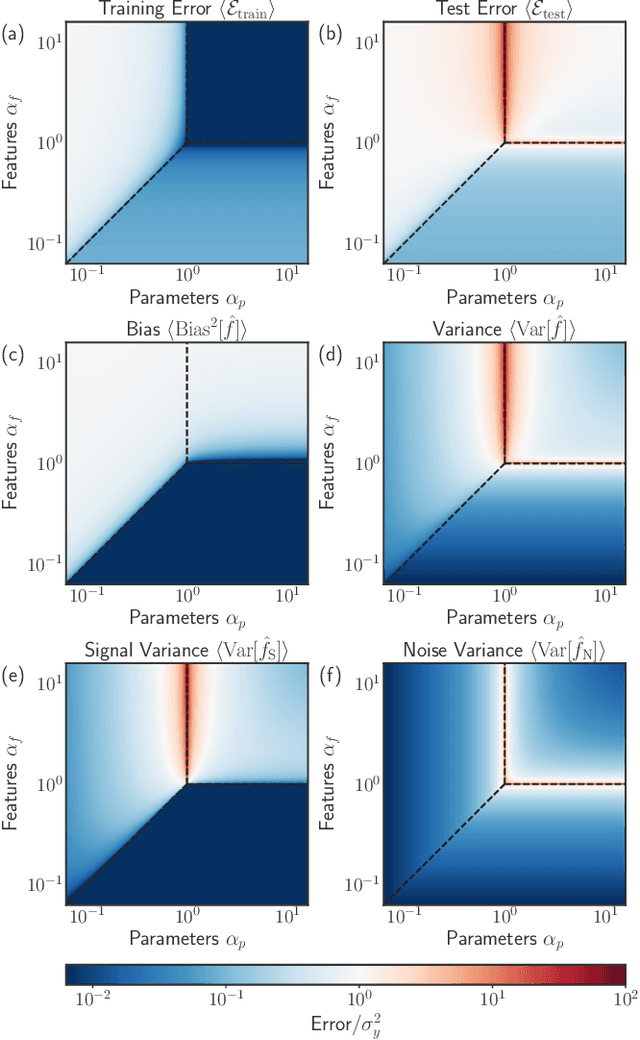
The bias-variance trade-off is a central concept in supervised learning. In classical statistics, increasing the complexity of a model (e.g., number of parameters) reduces bias but also increases variance. Until recently, it was commonly believed that optimal performance is achieved at intermediate model complexities which strike a balance between bias and variance. Modern Deep Learning methods flout this dogma, achieving state-of-the-art performance using "over-parameterized models" where the number of fit parameters is large enough to perfectly fit the training data. As a result, understanding bias and variance in over-parameterized models has emerged as a fundamental problem in machine learning. Here, we use methods from statistical physics to derive analytic expressions for bias and variance in three minimal models for over-parameterization (linear regression and two-layer neural networks with linear and nonlinear activation functions), allowing us to disentangle properties stemming from the model architecture and random sampling of data. All three models exhibit a phase transition to an interpolation regime where the training error is zero, with linear neural-networks possessing an additional phase transition between regimes with zero and nonzero bias. The test error diverges at the interpolation transition for all three models. However, beyond the transition, it decreases again for the neural network models due to a decrease in both bias and variance with model complexity. We also show that over-parameterized models can overfit even in the absence of noise. We synthesize these results to construct a holistic understanding of generalization error and the bias-variance trade-off in over-parameterized models.