Learning Memory Mechanisms for Decision Making through Demonstrations

In Partially Observable Markov Decision Processes, integrating an agent's history into memory poses a significant challenge for decision-making. Traditional imitation learning, relying on observation-action pairs for expert demonstrations, fails to capture the expert's memory mechanisms used in decision-making. To capture memory processes as demonstrations, we introduce the concept of memory dependency pairs $(p, q)$ indicating that events at time $p$ are recalled for decision-making at time $q$. We introduce AttentionTuner to leverage memory dependency pairs in Transformers and find significant improvements across several tasks compared to standard Transformers when evaluated on Memory Gym and the Long-term Memory Benchmark. Code is available at https://github.com/WilliamYue37/AttentionTuner.

Permutation Invariant Learning with High-Dimensional Particle Filters

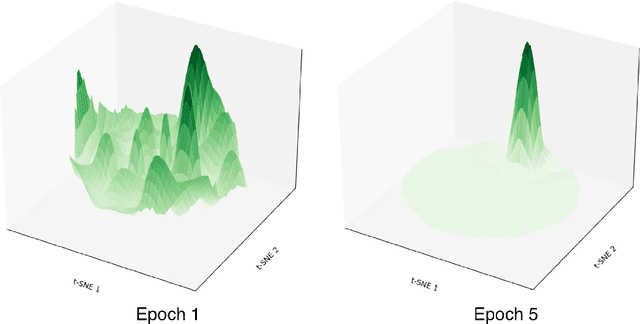
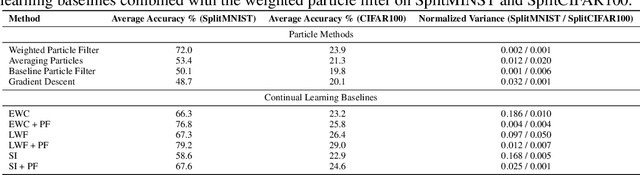
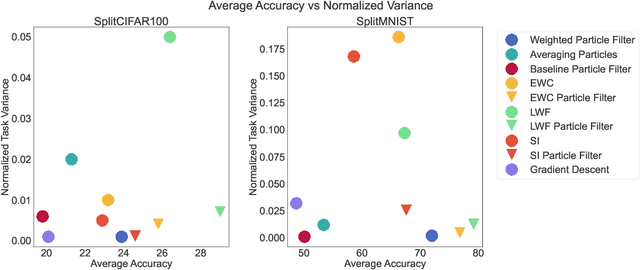
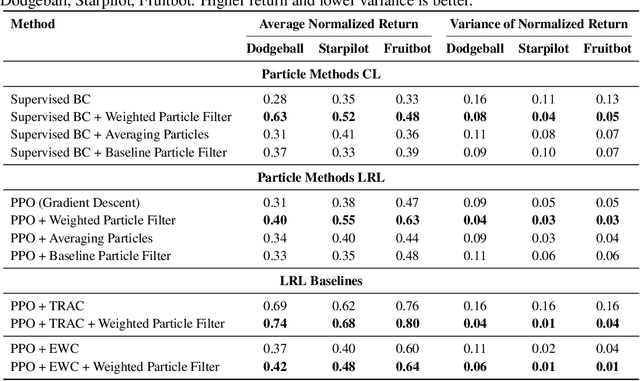
Sequential learning in deep models often suffers from challenges such as catastrophic forgetting and loss of plasticity, largely due to the permutation dependence of gradient-based algorithms, where the order of training data impacts the learning outcome. In this work, we introduce a novel permutation-invariant learning framework based on high-dimensional particle filters. We theoretically demonstrate that particle filters are invariant to the sequential ordering of training minibatches or tasks, offering a principled solution to mitigate catastrophic forgetting and loss-of-plasticity. We develop an efficient particle filter for optimizing high-dimensional models, combining the strengths of Bayesian methods with gradient-based optimization. Through extensive experiments on continual supervised and reinforcement learning benchmarks, including SplitMNIST, SplitCIFAR100, and ProcGen, we empirically show that our method consistently improves performance, while reducing variance compared to standard baselines.

Breaking Neural Network Scaling Laws with Modularity

Modular neural networks outperform nonmodular neural networks on tasks ranging from visual question answering to robotics. These performance improvements are thought to be due to modular networks' superior ability to model the compositional and combinatorial structure of real-world problems. However, a theoretical explanation of how modularity improves generalizability, and how to leverage task modularity while training networks remains elusive. Using recent theoretical progress in explaining neural network generalization, we investigate how the amount of training data required to generalize on a task varies with the intrinsic dimensionality of a task's input. We show theoretically that when applied to modularly structured tasks, while nonmodular networks require an exponential number of samples with task dimensionality, modular networks' sample complexity is independent of task dimensionality: modular networks can generalize in high dimensions. We then develop a novel learning rule for modular networks to exploit this advantage and empirically show the improved generalization of the rule, both in- and out-of-distribution, on high-dimensional, modular tasks.

Towards Exact Computation of Inductive Bias

Much research in machine learning involves finding appropriate inductive biases (e.g. convolutional neural networks, momentum-based optimizers, transformers) to promote generalization on tasks. However, quantification of the amount of inductive bias associated with these architectures and hyperparameters has been limited. We propose a novel method for efficiently computing the inductive bias required for generalization on a task with a fixed training data budget; formally, this corresponds to the amount of information required to specify well-generalizing models within a specific hypothesis space of models. Our approach involves modeling the loss distribution of random hypotheses drawn from a hypothesis space to estimate the required inductive bias for a task relative to these hypotheses. Unlike prior work, our method provides a direct estimate of inductive bias without using bounds and is applicable to diverse hypothesis spaces. Moreover, we derive approximation error bounds for our estimation approach in terms of the number of sampled hypotheses. Consistent with prior results, our empirical results demonstrate that higher dimensional tasks require greater inductive bias. We show that relative to other expressive model classes, neural networks as a model class encode large amounts of inductive bias. Furthermore, our measure quantifies the relative difference in inductive bias between different neural network architectures. Our proposed inductive bias metric provides an information-theoretic interpretation of the benefits of specific model architectures for certain tasks and provides a quantitative guide to developing tasks requiring greater inductive bias, thereby encouraging the development of more powerful inductive biases.

Resampling-free Particle Filters in High-dimensions

State estimation is crucial for the performance and safety of numerous robotic applications. Among the suite of estimation techniques, particle filters have been identified as a powerful solution due to their non-parametric nature. Yet, in high-dimensional state spaces, these filters face challenges such as 'particle deprivation' which hinders accurate representation of the true posterior distribution. This paper introduces a novel resampling-free particle filter designed to mitigate particle deprivation by forgoing the traditional resampling step. This ensures a broader and more diverse particle set, especially vital in high-dimensional scenarios. Theoretically, our proposed filter is shown to offer a near-accurate representation of the desired posterior distribution in high-dimensional contexts. Empirically, the effectiveness of our approach is underscored through a high-dimensional synthetic state estimation task and a 6D pose estimation derived from videos. We posit that as robotic systems evolve with greater degrees of freedom, particle filters tailored for high-dimensional state spaces will be indispensable.

t-DGR: A Trajectory-Based Deep Generative Replay Method for Continual Learning in Decision Making

Deep generative replay has emerged as a promising approach for continual learning in decision-making tasks. This approach addresses the problem of catastrophic forgetting by leveraging the generation of trajectories from previously encountered tasks to augment the current dataset. However, existing deep generative replay methods for continual learning rely on autoregressive models, which suffer from compounding errors in the generated trajectories. In this paper, we propose a simple, scalable, and non-autoregressive method for continual learning in decision-making tasks using a generative model that generates task samples conditioned on the trajectory timestep. We evaluate our method on Continual World benchmarks and find that our approach achieves state-of-the-art performance on the average success rate metric among continual learning methods. Code is available at https://github.com/WilliamYue37/t-DGR .