Self-Assembly of a Biologically Plausible Learning Circuit

Over the last four decades, the amazing success of deep learning has been driven by the use of Stochastic Gradient Descent (SGD) as the main optimization technique. The default implementation for the computation of the gradient for SGD is backpropagation, which, with its variations, is used to this day in almost all computer implementations. From the perspective of neuroscientists, however, the consensus is that backpropagation is unlikely to be used by the brain. Though several alternatives have been discussed, none is so far supported by experimental evidence. Here we propose a circuit for updating the weights in a network that is biologically plausible, works as well as backpropagation, and leads to verifiable predictions about the anatomy and the physiology of a characteristic motif of four plastic synapses between ascending and descending cortical streams. A key prediction of our proposal is a surprising property of self-assembly of the basic circuit, emerging from initial random connectivity and heterosynaptic plasticity rules.

Explicit regularization and implicit bias in deep network classifiers trained with the square loss

Deep ReLU networks trained with the square loss have been observed to perform well in classification tasks. We provide here a theoretical justification based on analysis of the associated gradient flow. We show that convergence to a solution with the absolute minimum norm is expected when normalization techniques such as Batch Normalization (BN) or Weight Normalization (WN) are used together with Weight Decay (WD). The main property of the minimizers that bounds their expected error is the norm: we prove that among all the close-to-interpolating solutions, the ones associated with smaller Frobenius norms of the unnormalized weight matrices have better margin and better bounds on the expected classification error. With BN but in the absence of WD, the dynamical system is singular. Implicit dynamical regularization -- that is zero-initial conditions biasing the dynamics towards high margin solutions -- is also possible in the no-BN and no-WD case. The theory yields several predictions, including the role of BN and weight decay, aspects of Papyan, Han and Donoho's Neural Collapse and the constraints induced by BN on the network weights.

Hierarchically Local Tasks and Deep Convolutional Networks

The main success stories of deep learning, starting with ImageNet, depend on convolutional networks, which on certain tasks perform significantly better than traditional shallow classifiers, such as support vector machines. Is there something special about deep convolutional networks that other learning machines do not possess? Recent results in approximation theory have shown that there is an exponential advantage of deep convolutional-like networks in approximating functions with hierarchical locality in their compositional structure. These mathematical results, however, do not say which tasks are expected to have input-output functions with hierarchical locality. Among all the possible hierarchically local tasks in vision, text and speech we explore a few of them experimentally by studying how they are affected by disrupting locality in the input images. We also discuss a taxonomy of tasks ranging from local, to hierarchically local, to global and make predictions about the type of networks required to perform efficiently on these different types of tasks.

Theoretical Issues in Deep Networks: Approximation, Optimization and Generalization

While deep learning is successful in a number of applications, it is not yet well understood theoretically. A satisfactory theoretical characterization of deep learning however, is beginning to emerge. It covers the following questions: 1) representation power of deep networks 2) optimization of the empirical risk 3) generalization properties of gradient descent techniques --- why the expected error does not suffer, despite the absence of explicit regularization, when the networks are overparametrized? In this review we discuss recent advances in the three areas. In approximation theory both shallow and deep networks have been shown to approximate any continuous functions on a bounded domain at the expense of an exponential number of parameters (exponential in the dimensionality of the function). However, for a subset of compositional functions, deep networks of the convolutional type can have a linear dependence on dimensionality, unlike shallow networks. In optimization we discuss the loss landscape for the exponential loss function and show that stochastic gradient descent will find with high probability the global minima. To address the question of generalization for classification tasks, we use classical uniform convergence results to justify minimizing a surrogate exponential-type loss function under a unit norm constraint on the weight matrix at each layer -- since the interesting variables for classification are the weight directions rather than the weights. Our approach, which is supported by several independent new results, offers a solution to the puzzle about generalization performance of deep overparametrized ReLU networks, uncovering the origin of the underlying hidden complexity control.

Theory III: Dynamics and Generalization in Deep Networks - a simple solution

We review recent observations on the dynamical systems induced by gradient descent (GD) methods used for training deep networks and summarize properties of the solutions they converge to. Recent results illuminate the absence of overfitting in the special case of linear networks for binary classification. They prove that minimization of loss functions such as the logistic, the cross-entropy and the exponential loss yields asymptotic convergence to the maximum margin solution for linearly separable datasets, independently of the initial conditions. Here we discuss the case of nonlinear DNNs near zero minima of the empirical loss, under exponential-type and square losses, for several variations of the basic GD algorithm, including a new NMGD version that converges to the minimum norm fixed points. Our main results are: 1) GD algorithms with weight normalization constraint achieve generalization; 2) the fundamental reason for the effectiveness of existing weight and batch normalization techniques is that they are approximate implementations of maximizing the margin under unit norm constraint; 3) even without explicit unit norm constraints, generalization can still be obtained for not-too-deep networks because standard GD is intrinsically consistent with the dynamics of normalized weights. In addition, the balance of the weights across different layers, if present at initialization, is maintained by the gradient flow. In the perspective of these theoretical results, we discuss experimental evidence around the apparent absence of overfitting, that is the observation that the expected classification error does not get worse when increasing the number of parameters. Our explanation focuses on the implicit normalization enforced by algorithms such as batch normalization. In particular, the control of the norm of the weights is related to Halpern iterations for minimum norm solutions.

Biologically-plausible learning algorithms can scale to large datasets

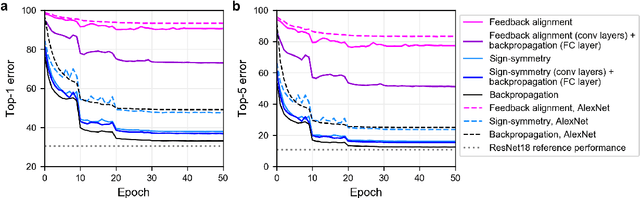
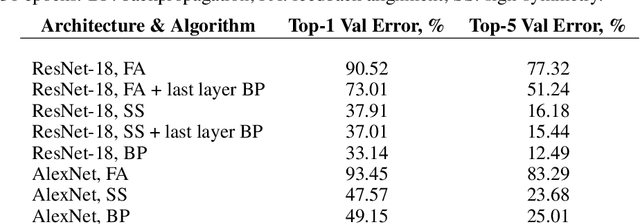
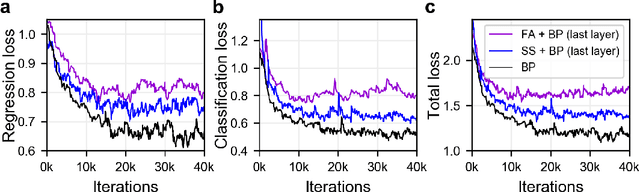
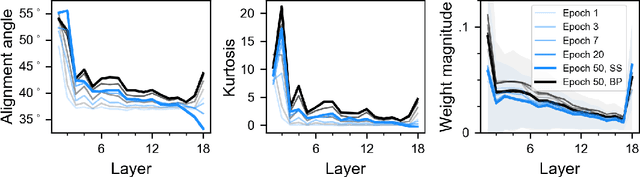
The backpropagation (BP) algorithm is often thought to be biologically implausible in the brain. One of the main reasons is that BP requires symmetric weight matrices in the feedforward and feedback pathways. To address this "weight transport problem" (Grossberg, 1987), two more biologically plausible algorithms, proposed by Liao et al. (2016) and Lillicrap et al. (2016), relax BP's weight symmetry requirements and demonstrate comparable learning capabilities to that of BP on small datasets. However, a recent study by Bartunov et al. (2018) evaluate variants of target-propagation (TP) and feedback alignment (FA) on MINIST, CIFAR, and ImageNet datasets, and find that although many of the proposed algorithms perform well on MNIST and CIFAR, they perform significantly worse than BP on ImageNet. Here, we additionally evaluate the sign-symmetry algorithm (Liao et al., 2016), which differs from both BP and FA in that the feedback and feedforward weights share signs but not magnitudes. We examine the performance of sign-symmetry and feedback alignment on ImageNet and MS COCO datasets using different network architectures (ResNet-18 and AlexNet for ImageNet, RetinaNet for MS COCO). Surprisingly, networks trained with sign-symmetry can attain classification performance approaching that of BP-trained networks. These results complement the study by Bartunov et al. (2018), and establish a new benchmark for future biologically plausible learning algorithms on more difficult datasets and more complex architectures.

A Surprising Linear Relationship Predicts Test Performance in Deep Networks

Given two networks with the same training loss on a dataset, when would they have drastically different test losses and errors? Better understanding of this question of generalization may improve practical applications of deep networks. In this paper we show that with cross-entropy loss it is surprisingly simple to induce significantly different generalization performances for two networks that have the same architecture, the same meta parameters and the same training error: one can either pretrain the networks with different levels of "corrupted" data or simply initialize the networks with weights of different Gaussian standard deviations. A corollary of recent theoretical results on overfitting shows that these effects are due to an intrinsic problem of measuring test performance with a cross-entropy/exponential-type loss, which can be decomposed into two components both minimized by SGD -- one of which is not related to expected classification performance. However, if we factor out this component of the loss, a linear relationship emerges between training and test losses. Under this transformation, classical generalization bounds are surprisingly tight: the empirical/training loss is very close to the expected/test loss. Furthermore, the empirical relation between classification error and normalized cross-entropy loss seem to be approximately monotonic

Theory IIIb: Generalization in Deep Networks

A main puzzle of deep neural networks (DNNs) revolves around the apparent absence of "overfitting", defined in this paper as follows: the expected error does not get worse when increasing the number of neurons or of iterations of gradient descent. This is surprising because of the large capacity demonstrated by DNNs to fit randomly labeled data and the absence of explicit regularization. Recent results by Srebro et al. provide a satisfying solution of the puzzle for linear networks used in binary classification. They prove that minimization of loss functions such as the logistic, the cross-entropy and the exp-loss yields asymptotic, "slow" convergence to the maximum margin solution for linearly separable datasets, independently of the initial conditions. Here we prove a similar result for nonlinear multilayer DNNs near zero minima of the empirical loss. The result holds for exponential-type losses but not for the square loss. In particular, we prove that the weight matrix at each layer of a deep network converges to a minimum norm solution up to a scale factor (in the separable case). Our analysis of the dynamical system corresponding to gradient descent of a multilayer network suggests a simple criterion for ranking the generalization performance of different zero minimizers of the empirical loss.

Theory of Deep Learning III: explaining the non-overfitting puzzle

A main puzzle of deep networks revolves around the absence of overfitting despite large overparametrization and despite the large capacity demonstrated by zero training error on randomly labeled data. In this note, we show that the dynamics associated to gradient descent minimization of nonlinear networks is topologically equivalent, near the asymptotically stable minima of the empirical error, to linear gradient system in a quadratic potential with a degenerate (for square loss) or almost degenerate (for logistic or crossentropy loss) Hessian. The proposition depends on the qualitative theory of dynamical systems and is supported by numerical results. Our main propositions extend to deep nonlinear networks two properties of gradient descent for linear networks, that have been recently established (1) to be key to their generalization properties: 1. Gradient descent enforces a form of implicit regularization controlled by the number of iterations, and asymptotically converges to the minimum norm solution for appropriate initial conditions of gradient descent. This implies that there is usually an optimum early stopping that avoids overfitting of the loss. This property, valid for the square loss and many other loss functions, is relevant especially for regression. 2. For classification, the asymptotic convergence to the minimum norm solution implies convergence to the maximum margin solution which guarantees good classification error for "low noise" datasets. This property holds for loss functions such as the logistic and cross-entropy loss independently of the initial conditions. The robustness to overparametrization has suggestive implications for the robustness of the architecture of deep convolutional networks with respect to the curse of dimensionality.

Theory of Deep Learning IIb: Optimization Properties of SGD

In Theory IIb we characterize with a mix of theory and experiments the optimization of deep convolutional networks by Stochastic Gradient Descent. The main new result in this paper is theoretical and experimental evidence for the following conjecture about SGD: SGD concentrates in probability -- like the classical Langevin equation -- on large volume, "flat" minima, selecting flat minimizers which are with very high probability also global minimizers