Hrushikesh Mhaskar
Localized kernel method for separation of linear chirps
Jul 03, 2025
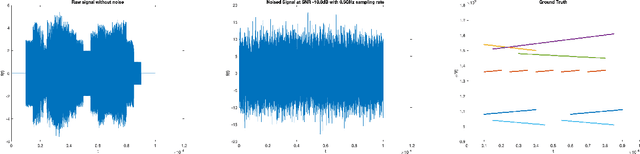
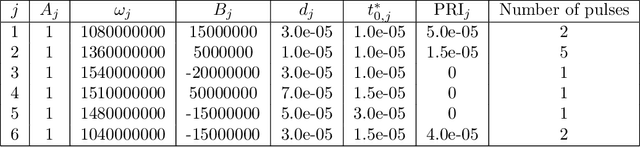
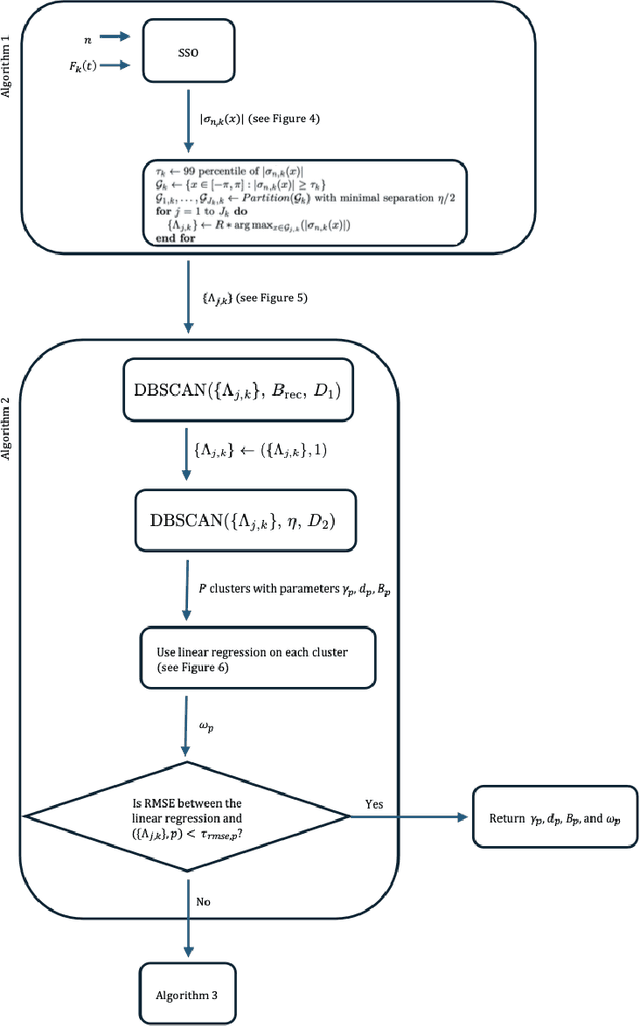
Abstract:The task of separating a superposition of signals into its individual components is a common challenge encountered in various signal processing applications, especially in domains such as audio and radar signals. A previous paper by Chui and Mhaskar proposes a method called Signal Separation Operator (SSO) to find the instantaneous frequencies and amplitudes of such superpositions where both of these change continuously and slowly over time. In this paper, we amplify and modify this method in order to separate chirp signals in the presence of crossovers, a very low SNR, and discontinuities. We give a theoretical analysis of the behavior of SSO in the presence of noise to examine the relationship between the minimal separation, minimal amplitude, SNR, and sampling frequency. Our method is illustrated with a few examples, and numerical results are reported on a simulated dataset comprising 7 simulated signals.
Active Learning Classification from a Signal Separation Perspective
Feb 23, 2025Abstract:In machine learning, classification is usually seen as a function approximation problem, where the goal is to learn a function that maps input features to class labels. In this paper, we propose a novel clustering and classification framework inspired by the principles of signal separation. This approach enables efficient identification of class supports, even in the presence of overlapping distributions. We validate our method on real-world hyperspectral datasets Salinas and Indian Pines. The experimental results demonstrate that our method is competitive with the state of the art active learning algorithms by using a very small subset of data set as training points.
Data Complexity Estimates for Operator Learning
May 25, 2024
Abstract:Operator learning has emerged as a new paradigm for the data-driven approximation of nonlinear operators. Despite its empirical success, the theoretical underpinnings governing the conditions for efficient operator learning remain incomplete. The present work develops theory to study the data complexity of operator learning, complementing existing research on the parametric complexity. We investigate the fundamental question: How many input/output samples are needed in operator learning to achieve a desired accuracy $\epsilon$? This question is addressed from the point of view of $n$-widths, and this work makes two key contributions. The first contribution is to derive lower bounds on $n$-widths for general classes of Lipschitz and Fr\'echet differentiable operators. These bounds rigorously demonstrate a ``curse of data-complexity'', revealing that learning on such general classes requires a sample size exponential in the inverse of the desired accuracy $\epsilon$. The second contribution of this work is to show that ``parametric efficiency'' implies ``data efficiency''; using the Fourier neural operator (FNO) as a case study, we show rigorously that on a narrower class of operators, efficiently approximated by FNO in terms of the number of tunable parameters, efficient operator learning is attainable in data complexity as well. Specifically, we show that if only an algebraically increasing number of tunable parameters is needed to reach a desired approximation accuracy, then an algebraically bounded number of data samples is also sufficient to achieve the same accuracy.
Tractability of approximation by general shallow networks
Aug 07, 2023Abstract:In this paper, we present a sharper version of the results in the paper Dimension independent bounds for general shallow networks; Neural Networks, \textbf{123} (2020), 142-152. Let $\mathbb{X}$ and $\mathbb{Y}$ be compact metric spaces. We consider approximation of functions of the form $ x\mapsto\int_{\mathbb{Y}} G( x, y)d\tau( y)$, $ x\in\mathbb{X}$, by $G$-networks of the form $ x\mapsto \sum_{k=1}^n a_kG( x, y_k)$, $ y_1,\cdots, y_n\in\mathbb{Y}$, $a_1,\cdots, a_n\in\mathbb{R}$. Defining the dimensions of $\mathbb{X}$ and $\mathbb{Y}$ in terms of covering numbers, we obtain dimension independent bounds on the degree of approximation in terms of $n$, where also the constants involved are all dependent at most polynomially on the dimensions. Applications include approximation by power rectified linear unit networks, zonal function networks, certain radial basis function networks as well as the important problem of function extension to higher dimensional spaces.
Approximation by non-symmetric networks for cross-domain learning
May 06, 2023Abstract:For the past 30 years or so, machine learning has stimulated a great deal of research in the study of approximation capabilities (expressive power) of a multitude of processes, such as approximation by shallow or deep neural networks, radial basis function networks, and a variety of kernel based methods. Motivated by applications such as invariant learning, transfer learning, and synthetic aperture radar imaging, we initiate in this paper a general approach to study the approximation capabilities of kernel based networks using non-symmetric kernels. While singular value decomposition is a natural instinct to study such kernels, we consider a more general approach to include the use of a family of kernels, such as generalized translation networks (which include neural networks and translation invariant kernels as special cases) and rotated zonal function kernels. Naturally, unlike traditional kernel based approximation, we cannot require the kernels to be positive definite. Our results apply to the approximation of functions with small smoothness compared to the dimension of the input space.
Encoding of data sets and algorithms
Mar 02, 2023Abstract:In many high-impact applications, it is important to ensure the quality of output of a machine learning algorithm as well as its reliability in comparison with the complexity of the algorithm used. In this paper, we have initiated a mathematically rigorous theory to decide which models (algorithms applied on data sets) are close to each other in terms of certain metrics, such as performance and the complexity level of the algorithm. This involves creating a grid on the hypothetical spaces of data sets and algorithms so as to identify a finite set of probability distributions from which the data sets are sampled and a finite set of algorithms. A given threshold metric acting on this grid will express the nearness (or statistical distance) from each algorithm and data set of interest to any given application. A technically difficult part of this project is to estimate the so-called metric entropy of a compact subset of functions of \textbf{infinitely many variables} that arise in the definition of these spaces.
Local approximation of operators
Feb 13, 2022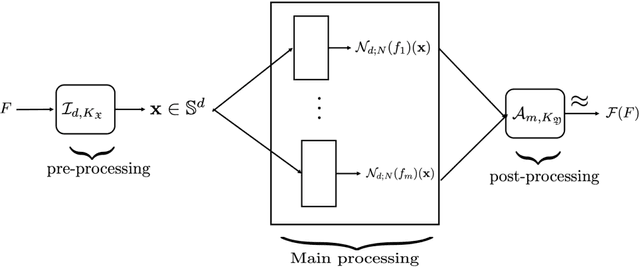
Abstract:Many applications, such as system identification, classification of time series, direct and inverse problems in partial differential equations, and uncertainty quantification lead to the question of approximation of a non-linear operator between metric spaces $\mathfrak{X}$ and $\mathfrak{Y}$. We study the problem of determining the degree of approximation of a such operators on a compact subset $K_\mathfrak{X}\subset \mathfrak{X}$ using a finite amount of information. If $\mathcal{F}: K_\mathfrak{X}\to K_\mathfrak{Y}$, a well established strategy to approximate $\mathcal{F}(F)$ for some $F\in K_\mathfrak{X}$ is to encode $F$ (respectively, $\mathcal{F}(F)$) in terms of a finite number $d$ (repectively $m$) of real numbers. Together with appropriate reconstruction algorithms (decoders), the problem reduces to the approximation of $m$ functions on a compact subset of a high dimensional Euclidean space $\mathbb{R}^d$, equivalently, the unit sphere $\mathbb{S}^d$ embedded in $\mathbb{R}^{d+1}$. The problem is challenging because $d$, $m$, as well as the complexity of the approximation on $\mathbb{S}^d$ are all large, and it is necessary to estimate the accuracy keeping track of the inter-dependence of all the approximations involved. In this paper, we establish constructive methods to do this efficiently; i.e., with the constants involved in the estimates on the approximation on $\\mathbb{S}^d$ being $\mathcal{O}(d^{1/6})$. We study different smoothness classes for the operators, and also propose a method for approximation of $\mathcal{F}(F)$ using only information in a small neighborhood of $F$, resulting in an effective reduction in the number of parameters involved. To further mitigate the problem of large number of parameters, we propose prefabricated networks, resulting in a substantially smaller number of effective parameters.
A manifold learning approach for gesture identification from micro-Doppler radar measurements
Oct 04, 2021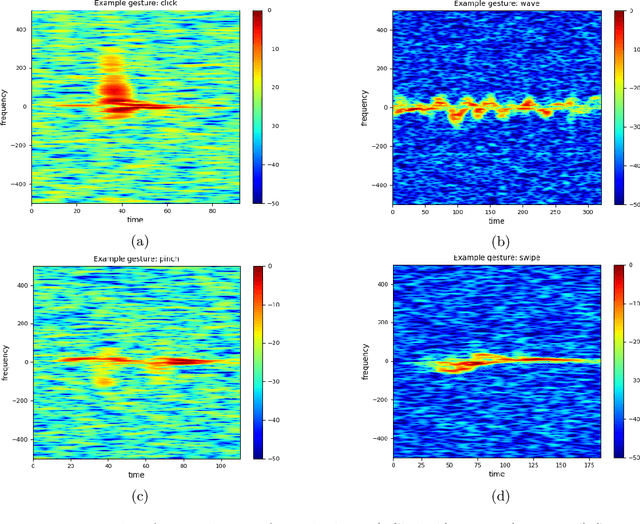
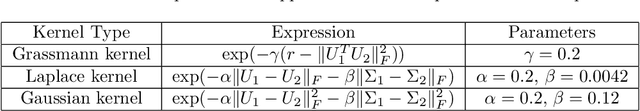
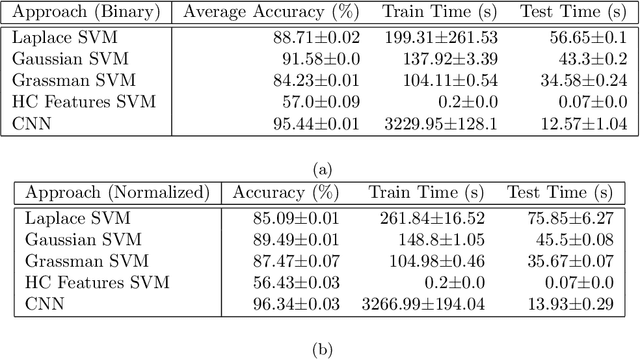

Abstract:A recent paper (Neural Networks, {\bf 132} (2020), 253-268) introduces a straightforward and simple kernel based approximation for manifold learning that does not require the knowledge of anything about the manifold, except for its dimension. In this paper, we examine the pointwise error in approximation using least squares optimization based on this kernel, in particular, how the error depends upon the data characteristics and deteriorates as one goes away from the training data. The theory is presented with an abstract localized kernel, which can utilize any prior knowledge about the data being located on an unknown sub-manifold of a known manifold. We demonstrate the performance of our approach using a publicly available micro-Doppler data set investigating the use of different pre-processing measures, kernels, and manifold dimension. Specifically, it is shown that the Gaussian kernel introduced in the above mentioned paper leads to a near-competitive performance to deep neural networks, and offers significant improvements in speed and memory requirements. Similarly, a kernel based on treating the feature space as a submanifold of the Grassman manifold outperforms conventional hand-crafted features. To demonstrate the fact that our methods are agnostic to the domain knowledge, we examine the classification problem in a simple video data set.
Kernel distance measures for time series, random fields and other structured data
Sep 29, 2021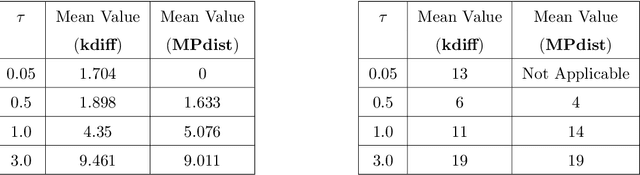
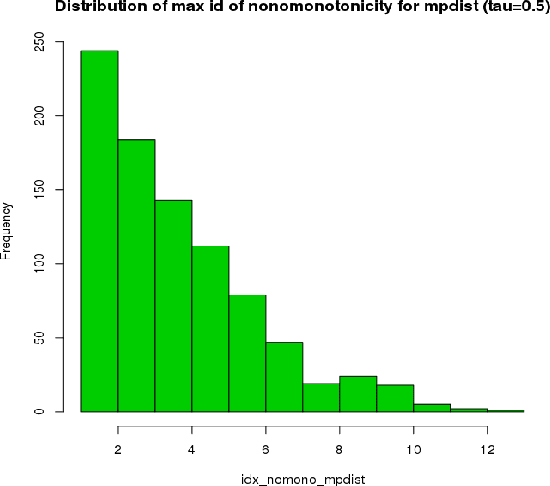
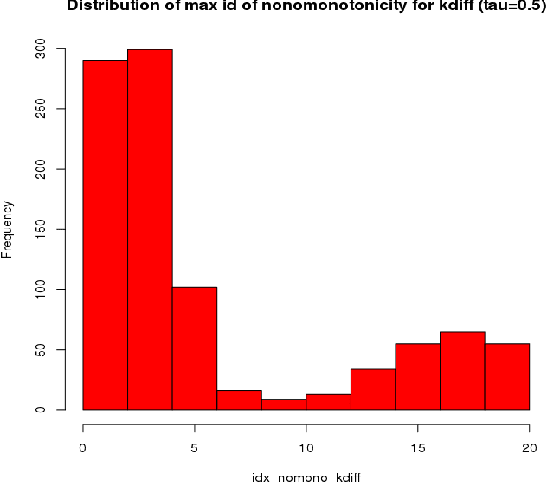
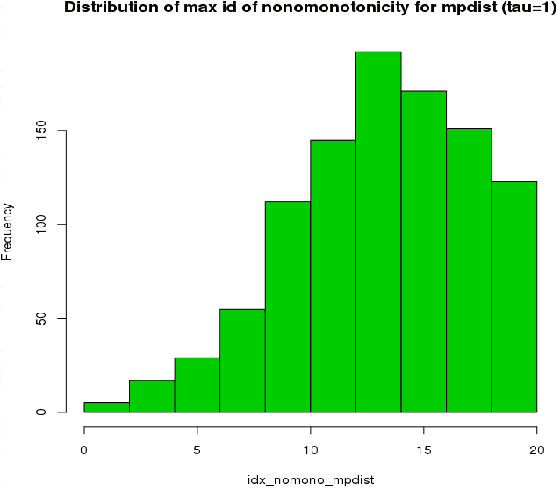
Abstract:This paper introduces kdiff, a novel kernel-based measure for estimating distances between instances of time series, random fields and other forms of structured data. This measure is based on the idea of matching distributions that only overlap over a portion of their region of support. Our proposed measure is inspired by MPdist which has been previously proposed for such datasets and is constructed using Euclidean metrics, whereas kdiff is constructed using non-linear kernel distances. Also, kdiff accounts for both self and cross similarities across the instances and is defined using a lower quantile of the distance distribution. Comparing the cross similarity to self similarity allows for measures of similarity that are more robust to noise and partial occlusions of the relevant signals. Our proposed measure kdiff is a more general form of the well known kernel-based Maximum Mean Discrepancy (MMD) distance estimated over the embeddings. Some theoretical results are provided for separability conditions using kdiff as a distance measure for clustering and classification problems where the embedding distributions can be modeled as two component mixtures. Applications are demonstrated for clustering of synthetic and real-life time series and image data, and the performance of kdiff is compared to competing distance measures for clustering.
Cautious Active Clustering
Aug 03, 2020

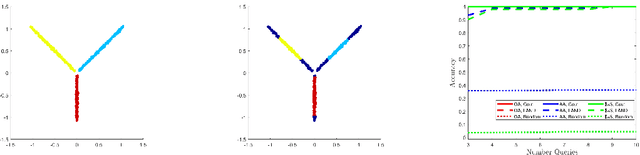

Abstract:We consider a set of points sampled from an unknown probability measure on a Euclidean space, each of which points belongs to one of the finitely many classes. We study the question of querying the class label at a very small number of judiciously chosen points so as to be able to attach the appropriate class label to every point in the set. Our approach is to consider the unknown probability measure as a convex combination of the conditional probabilities for each class. Our technique involves the use of a highly localized kernel constructed from Hermite polynomials, and use them to create a hierarchical estimate of the supports of the constituent probability measures. We do not need to make any assumptions on the nature of any of the probability measures nor know in advance the number of classes involved. We give theoretical guarantees measured by the $F$-score for our classification scheme. Examples include classification in hyper-spectral images, separation of distributions, and MNIST classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge