Katarina Doctor
Understanding and Estimating Domain Complexity Across Domains
Dec 20, 2023Abstract:Artificial Intelligence (AI) systems, trained in controlled environments, often struggle in real-world complexities. We propose a general framework for estimating domain complexity across diverse environments, like open-world learning and real-world applications. This framework distinguishes between intrinsic complexity (inherent to the domain) and extrinsic complexity (dependent on the AI agent). By analyzing dimensionality, sparsity, and diversity within these categories, we offer a comprehensive view of domain challenges. This approach enables quantitative predictions of AI difficulty during environment transitions, avoids bias in novel situations, and helps navigate the vast search spaces of open-world domains.
Toward Defining a Domain Complexity Measure Across Domains
Mar 07, 2023
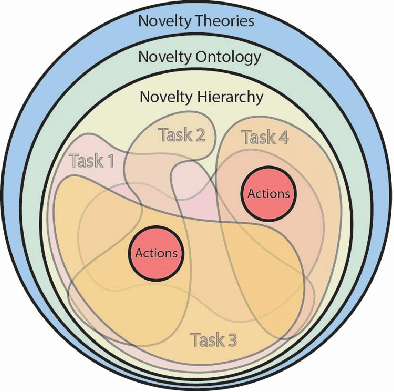


Abstract:Artificial Intelligence (AI) systems planned for deployment in real-world applications frequently are researched and developed in closed simulation environments where all variables are controlled and known to the simulator or labeled benchmark datasets are used. Transition from these simulators, testbeds, and benchmark datasets to more open-world domains poses significant challenges to AI systems, including significant increases in the complexity of the domain and the inclusion of real-world novelties; the open-world environment contains numerous out-of-distribution elements that are not part in the AI systems' training set. Here, we propose a path to a general, domain-independent measure of domain complexity level. We distinguish two aspects of domain complexity: intrinsic and extrinsic. The intrinsic domain complexity is the complexity that exists by itself without any action or interaction from an AI agent performing a task on that domain. This is an agent-independent aspect of the domain complexity. The extrinsic domain complexity is agent- and task-dependent. Intrinsic and extrinsic elements combined capture the overall complexity of the domain. We frame the components that define and impact domain complexity levels in a domain-independent light. Domain-independent measures of complexity could enable quantitative predictions of the difficulty posed to AI systems when transitioning from one testbed or environment to another, when facing out-of-distribution data in open-world tasks, and when navigating the rapidly expanding solution and search spaces encountered in open-world domains.
Encoding of data sets and algorithms
Mar 02, 2023Abstract:In many high-impact applications, it is important to ensure the quality of output of a machine learning algorithm as well as its reliability in comparison with the complexity of the algorithm used. In this paper, we have initiated a mathematically rigorous theory to decide which models (algorithms applied on data sets) are close to each other in terms of certain metrics, such as performance and the complexity level of the algorithm. This involves creating a grid on the hypothetical spaces of data sets and algorithms so as to identify a finite set of probability distributions from which the data sets are sampled and a finite set of algorithms. A given threshold metric acting on this grid will express the nearness (or statistical distance) from each algorithm and data set of interest to any given application. A technically difficult part of this project is to estimate the so-called metric entropy of a compact subset of functions of \textbf{infinitely many variables} that arise in the definition of these spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge