Understanding and Estimating Domain Complexity Across Domains

Artificial Intelligence (AI) systems, trained in controlled environments, often struggle in real-world complexities. We propose a general framework for estimating domain complexity across diverse environments, like open-world learning and real-world applications. This framework distinguishes between intrinsic complexity (inherent to the domain) and extrinsic complexity (dependent on the AI agent). By analyzing dimensionality, sparsity, and diversity within these categories, we offer a comprehensive view of domain challenges. This approach enables quantitative predictions of AI difficulty during environment transitions, avoids bias in novel situations, and helps navigate the vast search spaces of open-world domains.

Toward Defining a Domain Complexity Measure Across Domains

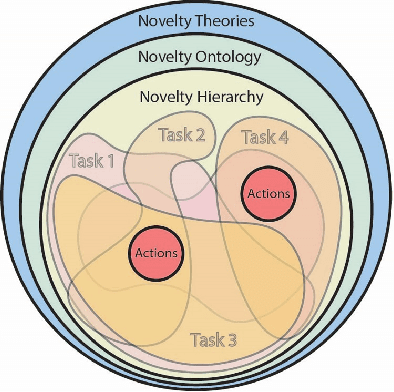
Artificial Intelligence (AI) systems planned for deployment in real-world applications frequently are researched and developed in closed simulation environments where all variables are controlled and known to the simulator or labeled benchmark datasets are used. Transition from these simulators, testbeds, and benchmark datasets to more open-world domains poses significant challenges to AI systems, including significant increases in the complexity of the domain and the inclusion of real-world novelties; the open-world environment contains numerous out-of-distribution elements that are not part in the AI systems' training set. Here, we propose a path to a general, domain-independent measure of domain complexity level. We distinguish two aspects of domain complexity: intrinsic and extrinsic. The intrinsic domain complexity is the complexity that exists by itself without any action or interaction from an AI agent performing a task on that domain. This is an agent-independent aspect of the domain complexity. The extrinsic domain complexity is agent- and task-dependent. Intrinsic and extrinsic elements combined capture the overall complexity of the domain. We frame the components that define and impact domain complexity levels in a domain-independent light. Domain-independent measures of complexity could enable quantitative predictions of the difficulty posed to AI systems when transitioning from one testbed or environment to another, when facing out-of-distribution data in open-world tasks, and when navigating the rapidly expanding solution and search spaces encountered in open-world domains.

Measuring the Complexity of Domains Used to Evaluate AI Systems

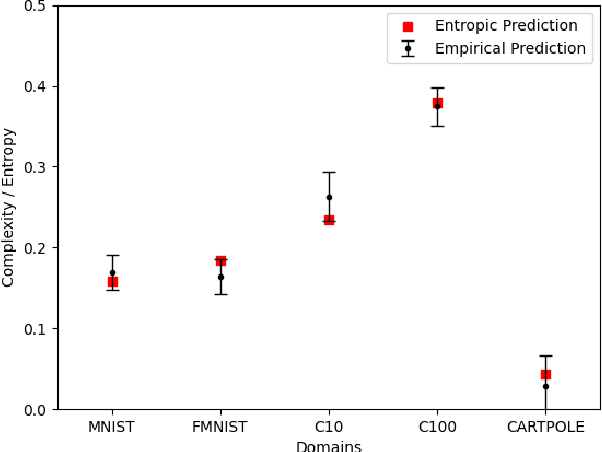
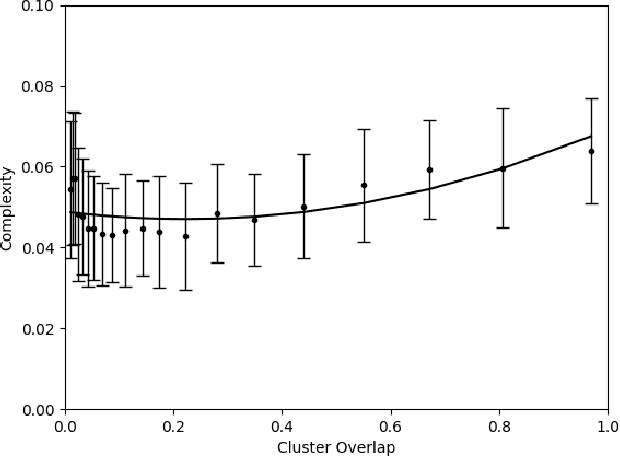
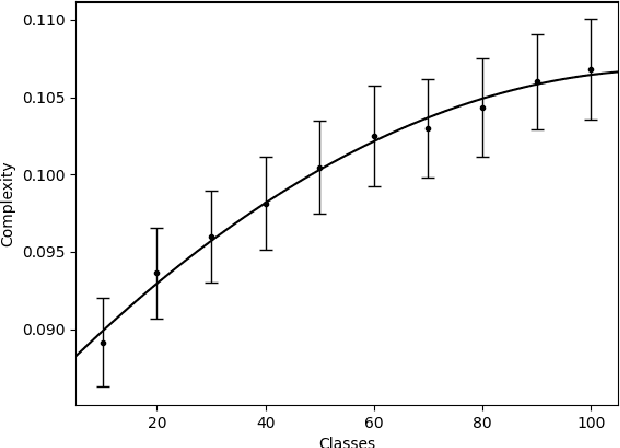
There is currently a rapid increase in the number of challenge problem, benchmarking datasets and algorithmic optimization tests for evaluating AI systems. However, there does not currently exist an objective measure to determine the complexity between these newly created domains. This lack of cross-domain examination creates an obstacle to effectively research more general AI systems. We propose a theory for measuring the complexity between varied domains. This theory is then evaluated using approximations by a population of neural network based AI systems. The approximations are compared to other well known standards and show it meets intuitions of complexity. An application of this measure is then demonstrated to show its effectiveness as a tool in varied situations. The experimental results show this measure has promise as an effective tool for aiding in the evaluation of AI systems. We propose the future use of such a complexity metric for use in computing an AI system's intelligence.

Fast Support Vector Machines Using Parallel Adaptive Shrinking on Distributed Systems

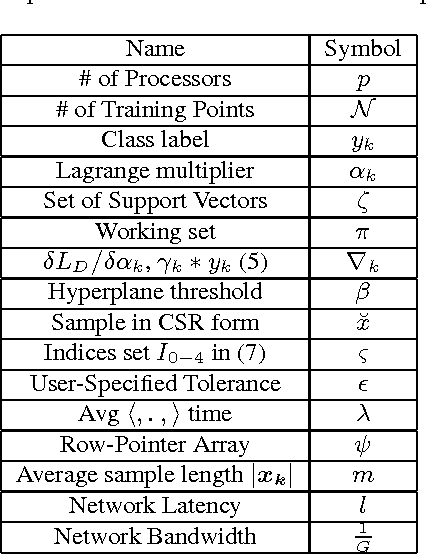
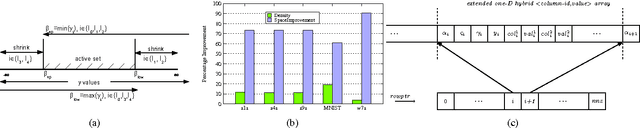
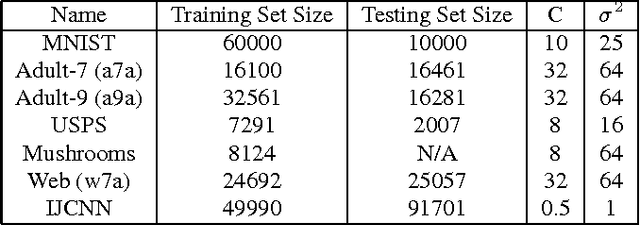
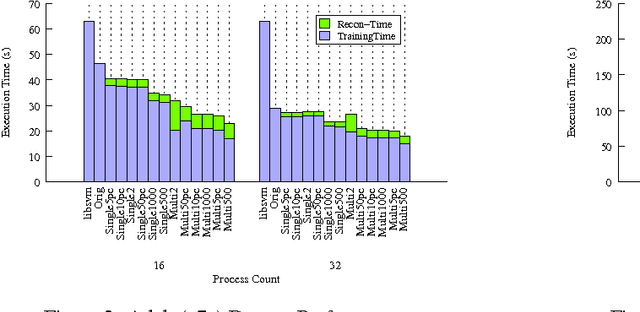
Support Vector Machines (SVM), a popular machine learning technique, has been applied to a wide range of domains such as science, finance, and social networks for supervised learning. Whether it is identifying high-risk patients by health-care professionals, or potential high-school students to enroll in college by school districts, SVMs can play a major role for social good. This paper undertakes the challenge of designing a scalable parallel SVM training algorithm for large scale systems, which includes commodity multi-core machines, tightly connected supercomputers and cloud computing systems. Intuitive techniques for improving the time-space complexity including adaptive elimination of samples for faster convergence and sparse format representation are proposed. Under sample elimination, several heuristics for {\em earliest possible} to {\em lazy} elimination of non-contributing samples are proposed. In several cases, where an early sample elimination might result in a false positive, low overhead mechanisms for reconstruction of key data structures are proposed. The algorithm and heuristics are implemented and evaluated on various publicly available datasets. Empirical evaluation shows up to 26x speed improvement on some datasets against the sequential baseline, when evaluated on multiple compute nodes, and an improvement in execution time up to 30-60\% is readily observed on a number of other datasets against our parallel baseline.