Cautious Active Clustering

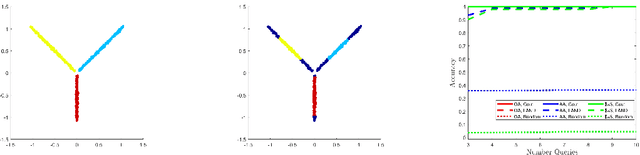
We consider a set of points sampled from an unknown probability measure on a Euclidean space, each of which points belongs to one of the finitely many classes. We study the question of querying the class label at a very small number of judiciously chosen points so as to be able to attach the appropriate class label to every point in the set. Our approach is to consider the unknown probability measure as a convex combination of the conditional probabilities for each class. Our technique involves the use of a highly localized kernel constructed from Hermite polynomials, and use them to create a hierarchical estimate of the supports of the constituent probability measures. We do not need to make any assumptions on the nature of any of the probability measures nor know in advance the number of classes involved. We give theoretical guarantees measured by the $F$-score for our classification scheme. Examples include classification in hyper-spectral images, separation of distributions, and MNIST classification.