A manifold learning approach for gesture identification from micro-Doppler radar measurements

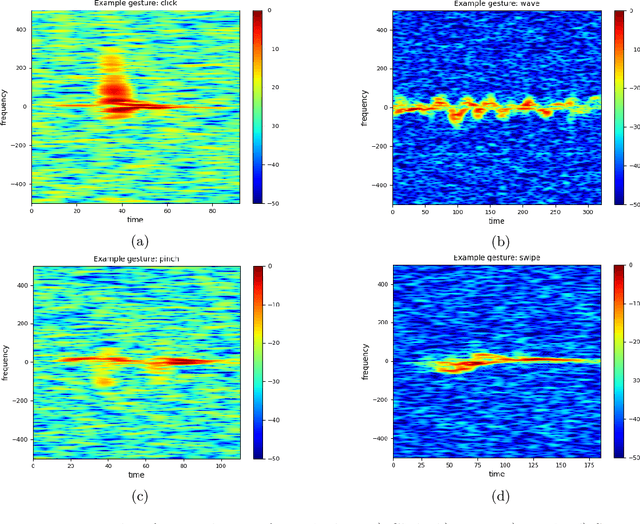
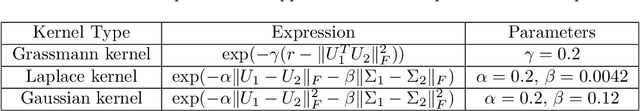
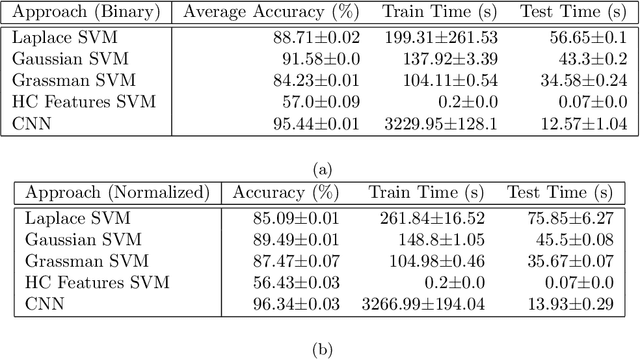
A recent paper (Neural Networks, {\bf 132} (2020), 253-268) introduces a straightforward and simple kernel based approximation for manifold learning that does not require the knowledge of anything about the manifold, except for its dimension. In this paper, we examine the pointwise error in approximation using least squares optimization based on this kernel, in particular, how the error depends upon the data characteristics and deteriorates as one goes away from the training data. The theory is presented with an abstract localized kernel, which can utilize any prior knowledge about the data being located on an unknown sub-manifold of a known manifold. We demonstrate the performance of our approach using a publicly available micro-Doppler data set investigating the use of different pre-processing measures, kernels, and manifold dimension. Specifically, it is shown that the Gaussian kernel introduced in the above mentioned paper leads to a near-competitive performance to deep neural networks, and offers significant improvements in speed and memory requirements. Similarly, a kernel based on treating the feature space as a submanifold of the Grassman manifold outperforms conventional hand-crafted features. To demonstrate the fact that our methods are agnostic to the domain knowledge, we examine the classification problem in a simple video data set.

Phase-Space Function Recovery for Moving Target Imaging in SAR by Convex Optimization

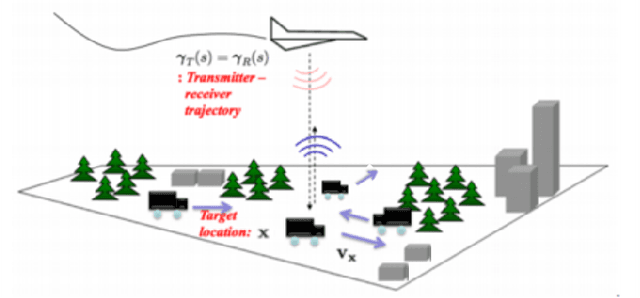
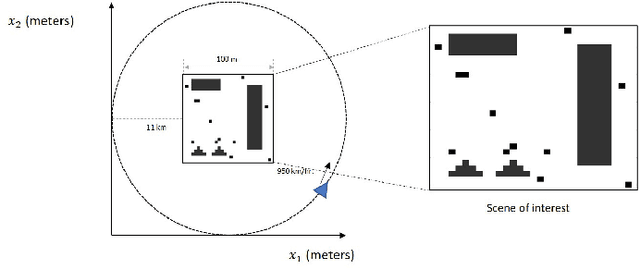
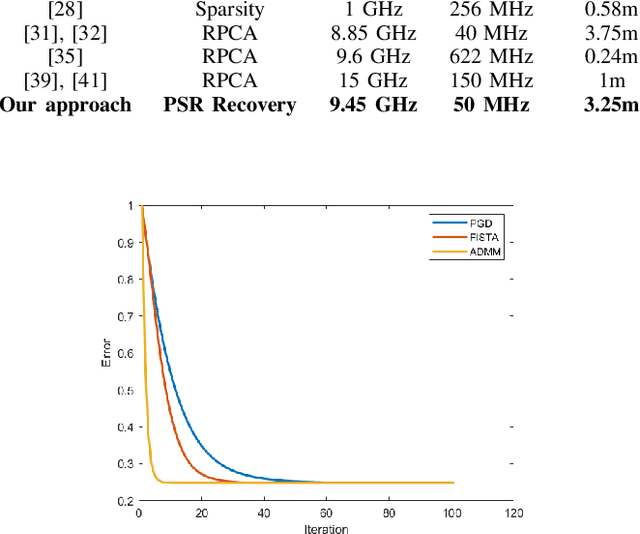
In this paper, we present an approach for ground moving target imaging (GMTI) and velocity recovery using synthetic aperture radar. We formulate the GMTI problem as the recovery of a phase-space reflectivity (PSR) function which represents the strengths and velocities of the scatterers in a scene of interest. We show that the discretized PSR matrix can be decomposed into a rank-one, and a highly sparse component corresponding to the stationary and moving scatterers, respectively. We then recover the two distinct components by solving a constrained optimization problem that admits computationally efficient convex solvers within the proximal gradient descent and alternating direction method of multipliers frameworks. Using the structural properties of the PSR matrix, we alleviate the computationally expensive steps associated with rank-constraints, such as singular value thresholding. Our optimization-based approach has several advantages over state-of-the-art GMTI methods, including computational efficiency, applicability to dense target environments, and arbitrary imaging configurations. We present extensive simulations to assess the robustness of our approach to both additive noise and clutter, with increasing number of moving targets. We show that both solvers perform well in dense moving target environments, and low-signal-to-clutter ratios without the need for additional clutter suppression techniques.

Deep Learning for Passive Synthetic Aperture Radar

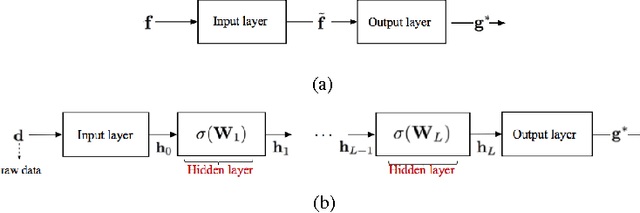
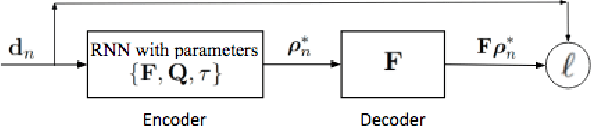
We introduce a deep learning (DL) framework for inverse problems in imaging, and demonstrate the advantages and applicability of this approach in passive synthetic aperture radar (SAR) image reconstruction. We interpret image recon- struction as a machine learning task and utilize deep networks as forward and inverse solvers for imaging. Specifically, we design a recurrent neural network (RNN) architecture as an inverse solver based on the iterations of proximal gradient descent optimization methods. We further adapt the RNN architecture to image reconstruction problems by transforming the network into a recurrent auto-encoder, thereby allowing for unsupervised training. Our DL based inverse solver is particularly suitable for a class of image formation problems in which the forward model is only partially known. The ability to learn forward models and hyper parameters combined with unsupervised training approach establish our recurrent auto-encoder suitable for real world applications. We demonstrate the performance of our method in passive SAR image reconstruction. In this regime a source of opportunity, with unknown location and transmitted waveform, is used to illuminate a scene of interest. We investigate recurrent auto- encoder architecture based on the 1 and 0 constrained least- squares problem. We present a projected stochastic gradient descent based training scheme which incorporates constraints of the unknown model parameters. We demonstrate through extensive numerical simulations that our DL based approach out performs conventional sparse coding methods in terms of computation and reconstructed image quality, specifically, when no information about the transmitter is available.