Kernel distance measures for time series, random fields and other structured data
Paper and Code
Sep 29, 2021
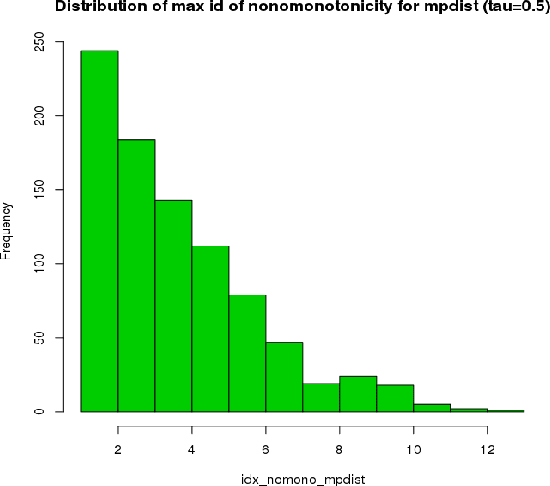
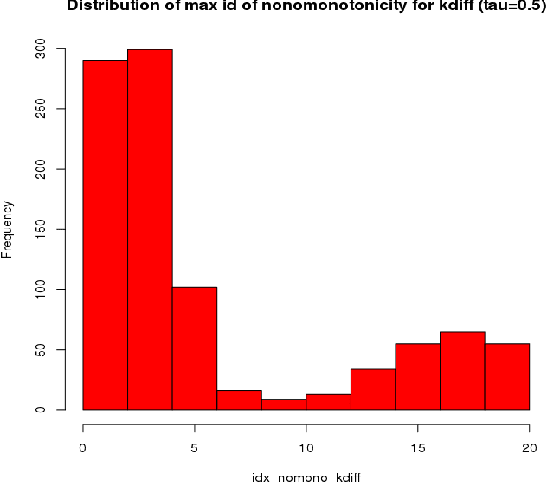
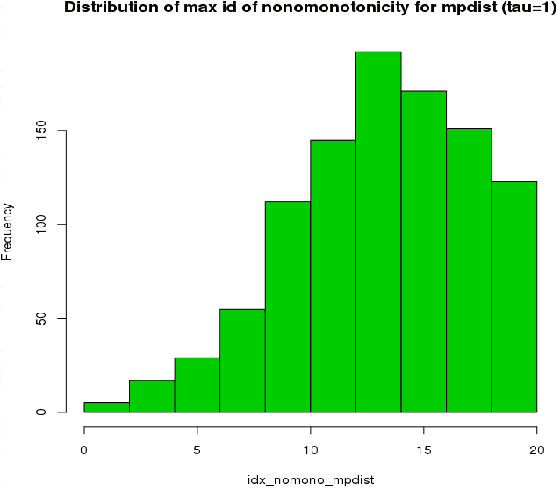
This paper introduces kdiff, a novel kernel-based measure for estimating distances between instances of time series, random fields and other forms of structured data. This measure is based on the idea of matching distributions that only overlap over a portion of their region of support. Our proposed measure is inspired by MPdist which has been previously proposed for such datasets and is constructed using Euclidean metrics, whereas kdiff is constructed using non-linear kernel distances. Also, kdiff accounts for both self and cross similarities across the instances and is defined using a lower quantile of the distance distribution. Comparing the cross similarity to self similarity allows for measures of similarity that are more robust to noise and partial occlusions of the relevant signals. Our proposed measure kdiff is a more general form of the well known kernel-based Maximum Mean Discrepancy (MMD) distance estimated over the embeddings. Some theoretical results are provided for separability conditions using kdiff as a distance measure for clustering and classification problems where the embedding distributions can be modeled as two component mixtures. Applications are demonstrated for clustering of synthetic and real-life time series and image data, and the performance of kdiff is compared to competing distance measures for clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge