Generative AI for fast and accurate Statistical Computation of Fluids

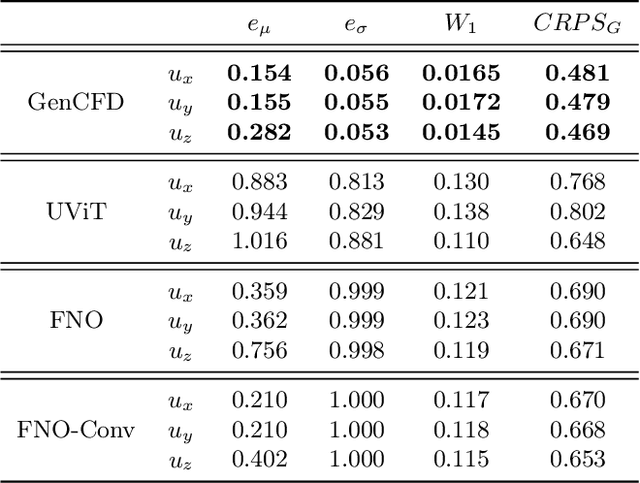
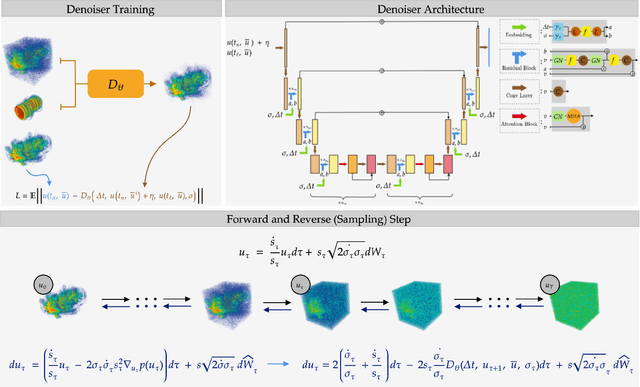
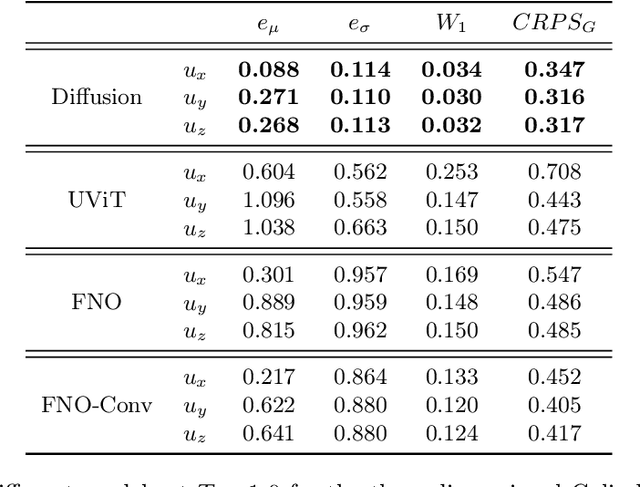
We present a generative AI algorithm for addressing the challenging task of fast, accurate and robust statistical computation of three-dimensional turbulent fluid flows. Our algorithm, termed as GenCFD, is based on a conditional score-based diffusion model. Through extensive numerical experimentation with both incompressible and compressible fluid flows, we demonstrate that GenCFD provides very accurate approximation of statistical quantities of interest such as mean, variance, point pdfs, higher-order moments, while also generating high quality realistic samples of turbulent fluid flows and ensuring excellent spectral resolution. In contrast, ensembles of operator learning baselines which are trained to minimize mean (absolute) square errors regress to the mean flow. We present rigorous theoretical results uncovering the surprising mechanisms through which diffusion models accurately generate fluid flows. These mechanisms are illustrated with solvable toy models that exhibit the relevant features of turbulent fluid flows while being amenable to explicit analytical formulas.

Operator Learning of Lipschitz Operators: An Information-Theoretic Perspective

Operator learning based on neural operators has emerged as a promising paradigm for the data-driven approximation of operators, mapping between infinite-dimensional Banach spaces. Despite significant empirical progress, our theoretical understanding regarding the efficiency of these approximations remains incomplete. This work addresses the parametric complexity of neural operator approximations for the general class of Lipschitz continuous operators. Motivated by recent findings on the limitations of specific architectures, termed curse of parametric complexity, we here adopt an information-theoretic perspective. Our main contribution establishes lower bounds on the metric entropy of Lipschitz operators in two approximation settings; uniform approximation over a compact set of input functions, and approximation in expectation, with input functions drawn from a probability measure. It is shown that these entropy bounds imply that, regardless of the activation function used, neural operator architectures attaining an approximation accuracy $\epsilon$ must have a size that is exponentially large in $\epsilon^{-1}$. The size of architectures is here measured by counting the number of encoded bits necessary to store the given model in computational memory. The results of this work elucidate fundamental trade-offs and limitations in

Data Complexity Estimates for Operator Learning

Operator learning has emerged as a new paradigm for the data-driven approximation of nonlinear operators. Despite its empirical success, the theoretical underpinnings governing the conditions for efficient operator learning remain incomplete. The present work develops theory to study the data complexity of operator learning, complementing existing research on the parametric complexity. We investigate the fundamental question: How many input/output samples are needed in operator learning to achieve a desired accuracy $\epsilon$? This question is addressed from the point of view of $n$-widths, and this work makes two key contributions. The first contribution is to derive lower bounds on $n$-widths for general classes of Lipschitz and Fr\'echet differentiable operators. These bounds rigorously demonstrate a ``curse of data-complexity'', revealing that learning on such general classes requires a sample size exponential in the inverse of the desired accuracy $\epsilon$. The second contribution of this work is to show that ``parametric efficiency'' implies ``data efficiency''; using the Fourier neural operator (FNO) as a case study, we show rigorously that on a narrower class of operators, efficiently approximated by FNO in terms of the number of tunable parameters, efficient operator learning is attainable in data complexity as well. Specifically, we show that if only an algebraically increasing number of tunable parameters is needed to reach a desired approximation accuracy, then an algebraically bounded number of data samples is also sufficient to achieve the same accuracy.

Discretization Error of Fourier Neural Operators

Operator learning is a variant of machine learning that is designed to approximate maps between function spaces from data. The Fourier Neural Operator (FNO) is a common model architecture used for operator learning. The FNO combines pointwise linear and nonlinear operations in physical space with pointwise linear operations in Fourier space, leading to a parameterized map acting between function spaces. Although FNOs formally involve convolutions of functions on a continuum, in practice the computations are performed on a discretized grid, allowing efficient implementation via the FFT. In this paper, the aliasing error that results from such a discretization is quantified and algebraic rates of convergence in terms of the grid resolution are obtained as a function of the regularity of the input. Numerical experiments that validate the theory and describe model stability are performed.

Operator Learning: Algorithms and Analysis

Operator learning refers to the application of ideas from machine learning to approximate (typically nonlinear) operators mapping between Banach spaces of functions. Such operators often arise from physical models expressed in terms of partial differential equations (PDEs). In this context, such approximate operators hold great potential as efficient surrogate models to complement traditional numerical methods in many-query tasks. Being data-driven, they also enable model discovery when a mathematical description in terms of a PDE is not available. This review focuses primarily on neural operators, built on the success of deep neural networks in the approximation of functions defined on finite dimensional Euclidean spaces. Empirically, neural operators have shown success in a variety of applications, but our theoretical understanding remains incomplete. This review article summarizes recent progress and the current state of our theoretical understanding of neural operators, focusing on an approximation theoretic point of view.

The curse of dimensionality in operator learning

Neural operator architectures employ neural networks to approximate operators mapping between Banach spaces of functions; they may be used to accelerate model evaluations via emulation, or to discover models from data. Consequently, the methodology has received increasing attention over recent years, giving rise to the rapidly growing field of operator learning. The first contribution of this paper is to prove that for general classes of operators which are characterized only by their $C^r$- or Lipschitz-regularity, operator learning suffers from a curse of dimensionality, defined precisely here in terms of representations of the infinite-dimensional input and output function spaces. The result is applicable to a wide variety of existing neural operators, including PCA-Net, DeepONet and the FNO. The second contribution of the paper is to prove that the general curse of dimensionality can be overcome for solution operators defined by the Hamilton-Jacobi equation; this is achieved by leveraging additional structure in the underlying solution operator, going beyond regularity. To this end, a novel neural operator architecture is introduced, termed HJ-Net, which explicitly takes into account characteristic information of the underlying Hamiltonian system. Error and complexity estimates are derived for HJ-Net which show that this architecture can provably beat the curse of dimensionality related to the infinite-dimensional input and output function spaces.

Error Bounds for Learning with Vector-Valued Random Features

This paper provides a comprehensive error analysis of learning with vector-valued random features (RF). The theory is developed for RF ridge regression in a fully general infinite-dimensional input-output setting, but nonetheless applies to and improves existing finite-dimensional analyses. In contrast to comparable work in the literature, the approach proposed here relies on a direct analysis of the underlying risk functional and completely avoids the explicit RF ridge regression solution formula in terms of random matrices. This removes the need for concentration results in random matrix theory or their generalizations to random operators. The main results established in this paper include strong consistency of vector-valued RF estimators under model misspecification and minimax optimal convergence rates in the well-specified setting. The parameter complexity (number of random features) and sample complexity (number of labeled data) required to achieve such rates are comparable with Monte Carlo intuition and free from logarithmic factors.

Neural Oscillators are Universal

Coupled oscillators are being increasingly used as the basis of machine learning (ML) architectures, for instance in sequence modeling, graph representation learning and in physical neural networks that are used in analog ML devices. We introduce an abstract class of neural oscillators that encompasses these architectures and prove that neural oscillators are universal, i.e, they can approximate any continuous and casual operator mapping between time-varying functions, to desired accuracy. This universality result provides theoretical justification for the use of oscillator based ML systems. The proof builds on a fundamental result of independent interest, which shows that a combination of forced harmonic oscillators with a nonlinear read-out suffices to approximate the underlying operators.

The Nonlocal Neural Operator: Universal Approximation

Neural operator architectures approximate operators between infinite-dimensional Banach spaces of functions. They are gaining increased attention in computational science and engineering, due to their potential both to accelerate traditional numerical methods and to enable data-driven discovery. A popular variant of neural operators is the Fourier neural operator (FNO). Previous analysis proving universal operator approximation theorems for FNOs resorts to use of an unbounded number of Fourier modes and limits the basic form of the method to problems with periodic geometry. Prior work relies on intuition from traditional numerical methods, and interprets the FNO as a nonstandard and highly nonlinear spectral method. The present work challenges this point of view in two ways: (i) the work introduces a new broad class of operator approximators, termed nonlocal neural operators (NNOs), which allow for operator approximation between functions defined on arbitrary geometries, and includes the FNO as a special case; and (ii) analysis of the NNOs shows that, provided this architecture includes computation of a spatial average (corresponding to retaining only a single Fourier mode in the special case of the FNO) it benefits from universal approximation. It is demonstrated that this theoretical result unifies the analysis of a wide range of neural operator architectures. Furthermore, it sheds new light on the role of nonlocality, and its interaction with nonlinearity, thereby paving the way for a more systematic exploration of nonlocality, both through the development of new operator learning architectures and the analysis of existing and new architectures.

Operator learning with PCA-Net: upper and lower complexity bounds

PCA-Net is a recently proposed neural operator architecture which combines principal component analysis (PCA) with neural networks to approximate operators between infinite-dimensional function spaces. The present work develops approximation theory for this approach, improving and significantly extending previous work in this direction: First, a novel universal approximation result is derived, under minimal assumptions on the underlying operator and the data-generating distribution. Then, two potential obstacles to efficient operator learning with PCA-Net are identified, and made precise through lower complexity bounds; the first relates to the complexity of the output distribution, measured by a slow decay of the PCA eigenvalues. The other obstacle relates to the inherent complexity of the space of operators between infinite-dimensional input and output spaces, resulting in a rigorous and quantifiable statement of the curse of dimensionality. In addition to these lower bounds, upper complexity bounds are derived. A suitable smoothness criterion is shown to ensure an algebraic decay of the PCA eigenvalues. Furthermore, it is shown that PCA-Net can overcome the general curse of dimensionality for specific operators of interest, arising from the Darcy flow and the Navier-Stokes equations.