Solving Roughly Forced Nonlinear PDEs via Misspecified Kernel Methods and Neural Networks

We consider the use of Gaussian Processes (GPs) or Neural Networks (NNs) to numerically approximate the solutions to nonlinear partial differential equations (PDEs) with rough forcing or source terms, which commonly arise as pathwise solutions to stochastic PDEs. Kernel methods have recently been generalized to solve nonlinear PDEs by approximating their solutions as the maximum a posteriori estimator of GPs that are conditioned to satisfy the PDE at a finite set of collocation points. The convergence and error guarantees of these methods, however, rely on the PDE being defined in a classical sense and its solution possessing sufficient regularity to belong to the associated reproducing kernel Hilbert space. We propose a generalization of these methods to handle roughly forced nonlinear PDEs while preserving convergence guarantees with an oversmoothing GP kernel that is misspecified relative to the true solution's regularity. This is achieved by conditioning a regular GP to satisfy the PDE with a modified source term in a weak sense (when integrated against a finite number of test functions). This is equivalent to replacing the empirical $L^2$-loss on the PDE constraint by an empirical negative-Sobolev norm. We further show that this loss function can be used to extend physics-informed neural networks (PINNs) to stochastic equations, thereby resulting in a new NN-based variant termed Negative Sobolev Norm-PINN (NeS-PINN).

Memorization and Regularization in Generative Diffusion Models

Diffusion models have emerged as a powerful framework for generative modeling. At the heart of the methodology is score matching: learning gradients of families of log-densities for noisy versions of the data distribution at different scales. When the loss function adopted in score matching is evaluated using empirical data, rather than the population loss, the minimizer corresponds to the score of a time-dependent Gaussian mixture. However, use of this analytically tractable minimizer leads to data memorization: in both unconditioned and conditioned settings, the generative model returns the training samples. This paper contains an analysis of the dynamical mechanism underlying memorization. The analysis highlights the need for regularization to avoid reproducing the analytically tractable minimizer; and, in so doing, lays the foundations for a principled understanding of how to regularize. Numerical experiments investigate the properties of: (i) Tikhonov regularization; (ii) regularization designed to promote asymptotic consistency; and (iii) regularizations induced by under-parameterization of a neural network or by early stopping when training a neural network. These experiments are evaluated in the context of memorization, and directions for future development of regularization are highlighted.

Operator Learning Using Random Features: A Tool for Scientific Computing

Supervised operator learning centers on the use of training data, in the form of input-output pairs, to estimate maps between infinite-dimensional spaces. It is emerging as a powerful tool to complement traditional scientific computing, which may often be framed in terms of operators mapping between spaces of functions. Building on the classical random features methodology for scalar regression, this paper introduces the function-valued random features method. This leads to a supervised operator learning architecture that is practical for nonlinear problems yet is structured enough to facilitate efficient training through the optimization of a convex, quadratic cost. Due to the quadratic structure, the trained model is equipped with convergence guarantees and error and complexity bounds, properties that are not readily available for most other operator learning architectures. At its core, the proposed approach builds a linear combination of random operators. This turns out to be a low-rank approximation of an operator-valued kernel ridge regression algorithm, and hence the method also has strong connections to Gaussian process regression. The paper designs function-valued random features that are tailored to the structure of two nonlinear operator learning benchmark problems arising from parametric partial differential equations. Numerical results demonstrate the scalability, discretization invariance, and transferability of the function-valued random features method.

Autoencoders in Function Space

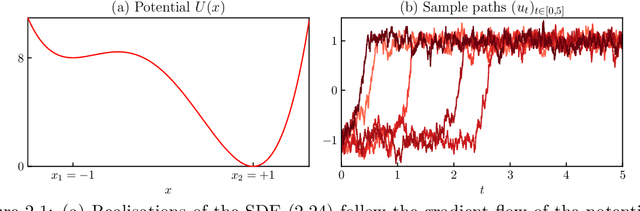
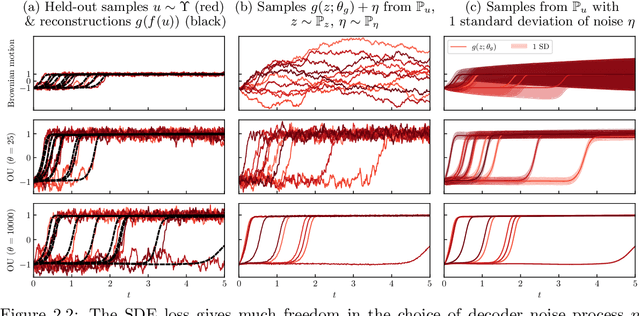
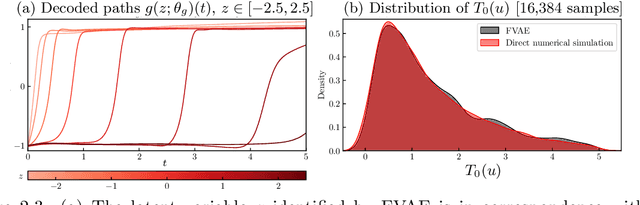
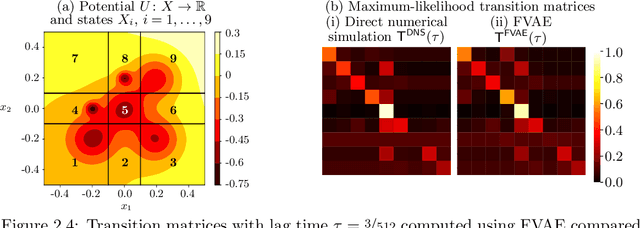
Autoencoders have found widespread application, in both their original deterministic form and in their variational formulation (VAEs). In scientific applications it is often of interest to consider data that are comprised of functions; the same perspective is useful in image processing. In practice, discretisation (of differential equations arising in the sciences) or pixellation (of images) renders problems finite dimensional, but conceiving first of algorithms that operate on functions, and only then discretising or pixellating, leads to better algorithms that smoothly operate between different levels of discretisation or pixellation. In this paper function-space versions of the autoencoder (FAE) and variational autoencoder (FVAE) are introduced, analysed, and deployed. Well-definedness of the objective function governing VAEs is a subtle issue, even in finite dimension, and more so on function space. The FVAE objective is well defined whenever the data distribution is compatible with the chosen generative model; this happens, for example, when the data arise from a stochastic differential equation. The FAE objective is valid much more broadly, and can be straightforwardly applied to data governed by differential equations. Pairing these objectives with neural operator architectures, which can thus be evaluated on any mesh, enables new applications of autoencoders to inpainting, superresolution, and generative modelling of scientific data.

Efficient, Multimodal, and Derivative-Free Bayesian Inference With Fisher-Rao Gradient Flows

In this paper, we study efficient approximate sampling for probability distributions known up to normalization constants. We specifically focus on a problem class arising in Bayesian inference for large-scale inverse problems in science and engineering applications. The computational challenges we address with the proposed methodology are: (i) the need for repeated evaluations of expensive forward models; (ii) the potential existence of multiple modes; and (iii) the fact that gradient of, or adjoint solver for, the forward model might not be feasible. While existing Bayesian inference methods meet some of these challenges individually, we propose a framework that tackles all three systematically. Our approach builds upon the Fisher-Rao gradient flow in probability space, yielding a dynamical system for probability densities that converges towards the target distribution at a uniform exponential rate. This rapid convergence is advantageous for the computational burden outlined in (i). We apply Gaussian mixture approximations with operator splitting techniques to simulate the flow numerically; the resulting approximation can capture multiple modes thus addressing (ii). Furthermore, we employ the Kalman methodology to facilitate a derivative-free update of these Gaussian components and their respective weights, addressing the issue in (iii). The proposed methodology results in an efficient derivative-free sampler flexible enough to handle multi-modal distributions: Gaussian Mixture Kalman Inversion (GMKI). The effectiveness of GMKI is demonstrated both theoretically and numerically in several experiments with multimodal target distributions, including proof-of-concept and two-dimensional examples, as well as a large-scale application: recovering the Navier-Stokes initial condition from solution data at positive times.

Continuum Attention for Neural Operators

Transformers, and the attention mechanism in particular, have become ubiquitous in machine learning. Their success in modeling nonlocal, long-range correlations has led to their widespread adoption in natural language processing, computer vision, and time-series problems. Neural operators, which map spaces of functions into spaces of functions, are necessarily both nonlinear and nonlocal if they are universal; it is thus natural to ask whether the attention mechanism can be used in the design of neural operators. Motivated by this, we study transformers in the function space setting. We formulate attention as a map between infinite dimensional function spaces and prove that the attention mechanism as implemented in practice is a Monte Carlo or finite difference approximation of this operator. The function space formulation allows for the design of transformer neural operators, a class of architectures designed to learn mappings between function spaces, for which we prove a universal approximation result. The prohibitive cost of applying the attention operator to functions defined on multi-dimensional domains leads to the need for more efficient attention-based architectures. For this reason we also introduce a function space generalization of the patching strategy from computer vision, and introduce a class of associated neural operators. Numerical results, on an array of operator learning problems, demonstrate the promise of our approaches to function space formulations of attention and their use in neural operators.

Efficient Prior Calibration From Indirect Data

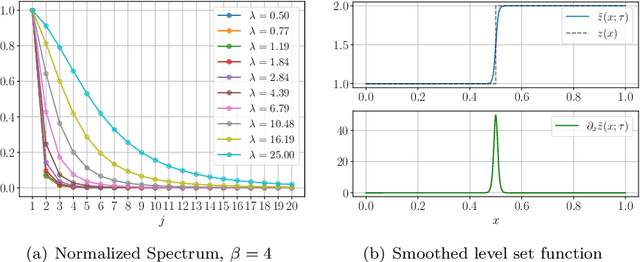
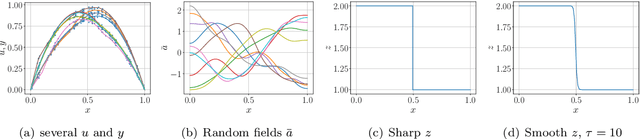
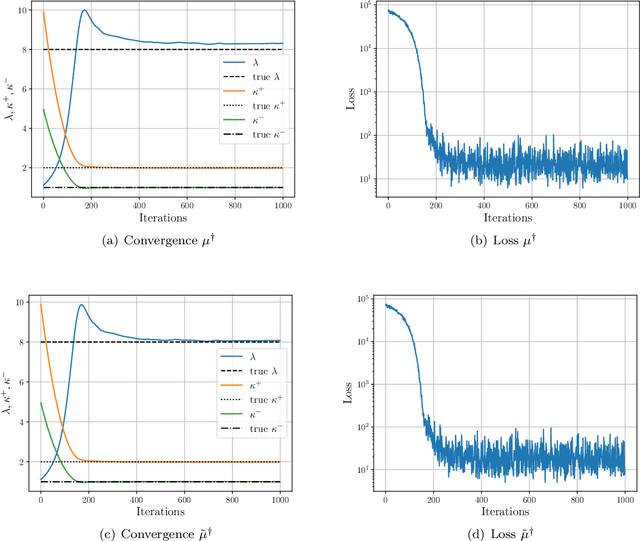
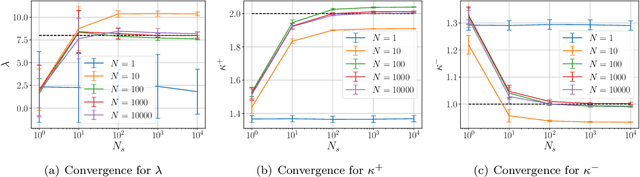
Bayesian inversion is central to the quantification of uncertainty within problems arising from numerous applications in science and engineering. To formulate the approach, four ingredients are required: a forward model mapping the unknown parameter to an element of a solution space, often the solution space for a differential equation; an observation operator mapping an element of the solution space to the data space; a noise model describing how noise pollutes the observations; and a prior model describing knowledge about the unknown parameter before the data is acquired. This paper is concerned with learning the prior model from data; in particular, learning the prior from multiple realizations of indirect data obtained through the noisy observation process. The prior is represented, using a generative model, as the pushforward of a Gaussian in a latent space; the pushforward map is learned by minimizing an appropriate loss function. A metric that is well-defined under empirical approximation is used to define the loss function for the pushforward map to make an implementable methodology. Furthermore, an efficient residual-based neural operator approximation of the forward model is proposed and it is shown that this may be learned concurrently with the pushforward map, using a bilevel optimization formulation of the problem; this use of neural operator approximation has the potential to make prior learning from indirect data more computationally efficient, especially when the observation process is expensive, non-smooth or not known. The ideas are illustrated with the Darcy flow inverse problem of finding permeability from piezometric head measurements.

Discretization Error of Fourier Neural Operators

Operator learning is a variant of machine learning that is designed to approximate maps between function spaces from data. The Fourier Neural Operator (FNO) is a common model architecture used for operator learning. The FNO combines pointwise linear and nonlinear operations in physical space with pointwise linear operations in Fourier space, leading to a parameterized map acting between function spaces. Although FNOs formally involve convolutions of functions on a continuum, in practice the computations are performed on a discretized grid, allowing efficient implementation via the FFT. In this paper, the aliasing error that results from such a discretization is quantified and algebraic rates of convergence in terms of the grid resolution are obtained as a function of the regularity of the input. Numerical experiments that validate the theory and describe model stability are performed.

Operator Learning: Algorithms and Analysis

Operator learning refers to the application of ideas from machine learning to approximate (typically nonlinear) operators mapping between Banach spaces of functions. Such operators often arise from physical models expressed in terms of partial differential equations (PDEs). In this context, such approximate operators hold great potential as efficient surrogate models to complement traditional numerical methods in many-query tasks. Being data-driven, they also enable model discovery when a mathematical description in terms of a PDE is not available. This review focuses primarily on neural operators, built on the success of deep neural networks in the approximation of functions defined on finite dimensional Euclidean spaces. Empirically, neural operators have shown success in a variety of applications, but our theoretical understanding remains incomplete. This review article summarizes recent progress and the current state of our theoretical understanding of neural operators, focusing on an approximation theoretic point of view.

Modeling groundwater levels in California's Central Valley by hierarchical Gaussian process and neural network regression

Modeling groundwater levels continuously across California's Central Valley (CV) hydrological system is challenging due to low-quality well data which is sparsely and noisily sampled across time and space. A novel machine learning method is proposed for modeling groundwater levels by learning from a 3D lithological texture model of the CV aquifer. The proposed formulation performs multivariate regression by combining Gaussian processes (GP) and deep neural networks (DNN). Proposed hierarchical modeling approach constitutes training the DNN to learn a lithologically informed latent space where non-parametric regression with GP is performed. The methodology is applied for modeling groundwater levels across the CV during 2015 - 2020. We demonstrate the efficacy of GP-DNN regression for modeling non-stationary features in the well data with fast and reliable uncertainty quantification. Our results indicate that the 2017 and 2019 wet years in California were largely ineffective in replenishing the groundwater loss caused during previous drought years.