Efficient Prior Calibration From Indirect Data
Paper and Code
May 28, 2024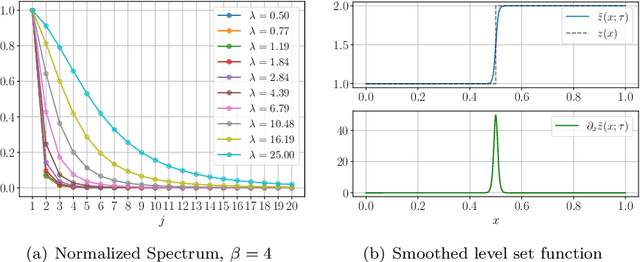
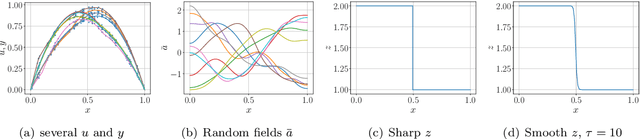
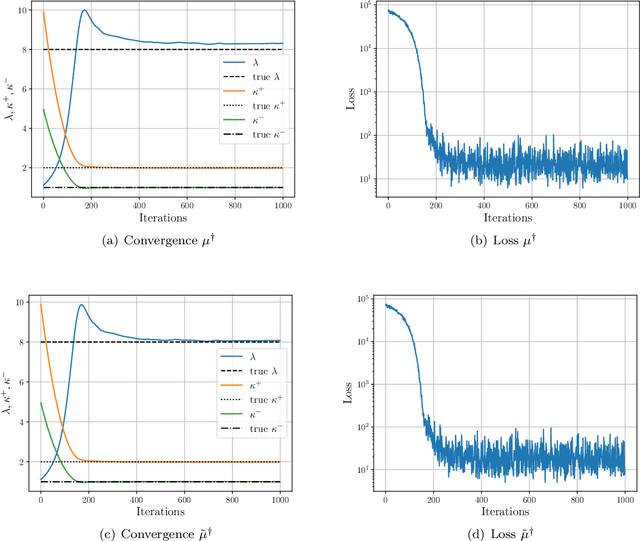
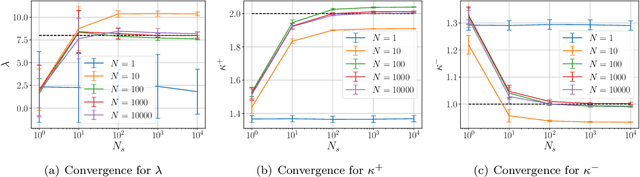
Bayesian inversion is central to the quantification of uncertainty within problems arising from numerous applications in science and engineering. To formulate the approach, four ingredients are required: a forward model mapping the unknown parameter to an element of a solution space, often the solution space for a differential equation; an observation operator mapping an element of the solution space to the data space; a noise model describing how noise pollutes the observations; and a prior model describing knowledge about the unknown parameter before the data is acquired. This paper is concerned with learning the prior model from data; in particular, learning the prior from multiple realizations of indirect data obtained through the noisy observation process. The prior is represented, using a generative model, as the pushforward of a Gaussian in a latent space; the pushforward map is learned by minimizing an appropriate loss function. A metric that is well-defined under empirical approximation is used to define the loss function for the pushforward map to make an implementable methodology. Furthermore, an efficient residual-based neural operator approximation of the forward model is proposed and it is shown that this may be learned concurrently with the pushforward map, using a bilevel optimization formulation of the problem; this use of neural operator approximation has the potential to make prior learning from indirect data more computationally efficient, especially when the observation process is expensive, non-smooth or not known. The ideas are illustrated with the Darcy flow inverse problem of finding permeability from piezometric head measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge