Continuum Attention for Neural Operators

Transformers, and the attention mechanism in particular, have become ubiquitous in machine learning. Their success in modeling nonlocal, long-range correlations has led to their widespread adoption in natural language processing, computer vision, and time-series problems. Neural operators, which map spaces of functions into spaces of functions, are necessarily both nonlinear and nonlocal if they are universal; it is thus natural to ask whether the attention mechanism can be used in the design of neural operators. Motivated by this, we study transformers in the function space setting. We formulate attention as a map between infinite dimensional function spaces and prove that the attention mechanism as implemented in practice is a Monte Carlo or finite difference approximation of this operator. The function space formulation allows for the design of transformer neural operators, a class of architectures designed to learn mappings between function spaces, for which we prove a universal approximation result. The prohibitive cost of applying the attention operator to functions defined on multi-dimensional domains leads to the need for more efficient attention-based architectures. For this reason we also introduce a function space generalization of the patching strategy from computer vision, and introduce a class of associated neural operators. Numerical results, on an array of operator learning problems, demonstrate the promise of our approaches to function space formulations of attention and their use in neural operators.

Hybrid Square Neural ODE Causal Modeling

Hybrid models combine mechanistic ODE-based dynamics with flexible and expressive neural network components. Such models have grown rapidly in popularity, especially in scientific domains where such ODE-based modeling offers important interpretability and validated causal grounding (e.g., for counterfactual reasoning). The incorporation of mechanistic models also provides inductive bias in standard blackbox modeling approaches, critical when learning from small datasets or partially observed, complex systems. Unfortunately, as hybrid models become more flexible, the causal grounding provided by the mechanistic model can quickly be lost. We address this problem by leveraging another common source of domain knowledge: ranking of treatment effects for a set of interventions, even if the precise treatment effect is unknown. We encode this information in a causal loss that we combine with the standard predictive loss to arrive at a hybrid loss that biases our learning towards causally valid hybrid models. We demonstrate our ability to achieve a win-win -- state-of-the-art predictive performance and causal validity -- in the challenging task of modeling glucose dynamics during exercise.

Learning About Structural Errors in Models of Complex Dynamical Systems

Complex dynamical systems are notoriously difficult to model because some degrees of freedom (e.g., small scales) may be computationally unresolvable or are incompletely understood, yet they are dynamically important. For example, the small scales of cloud dynamics and droplet formation are crucial for controlling climate, yet are unresolvable in global climate models. Semi-empirical closure models for the effects of unresolved degrees of freedom often exist and encode important domain-specific knowledge. Building on such closure models and correcting them through learning the structural errors can be an effective way of fusing data with domain knowledge. Here we describe a general approach, principles, and algorithms for learning about structural errors. Key to our approach is to include structural error models inside the models of complex systems, for example, in closure models for unresolved scales. The structural errors then map, usually nonlinearly, to observable data. As a result, however, mismatches between model output and data are only indirectly informative about structural errors, due to a lack of labeled pairs of inputs and outputs of structural error models. Additionally, derivatives of the model may not exist or be readily available. We discuss how structural error models can be learned from indirect data with derivative-free Kalman inversion algorithms and variants, how sparsity constraints enforce a "do no harm" principle, and various ways of modeling structural errors. We also discuss the merits of using non-local and/or stochastic error models. In addition, we demonstrate how data assimilation techniques can assist the learning about structural errors in non-ergodic systems. The concepts and algorithms are illustrated in two numerical examples based on the Lorenz-96 system and a human glucose-insulin model.

Learning Absorption Rates in Glucose-Insulin Dynamics from Meal Covariates

Traditional models of glucose-insulin dynamics rely on heuristic parameterizations chosen to fit observations within a laboratory setting. However, these models cannot describe glucose dynamics in daily life. One source of failure is in their descriptions of glucose absorption rates after meal events. A meal's macronutritional content has nuanced effects on the absorption profile, which is difficult to model mechanistically. In this paper, we propose to learn the effects of macronutrition content from glucose-insulin data and meal covariates. Given macronutrition information and meal times, we use a neural network to predict an individual's glucose absorption rate. We use this neural rate function as the control function in a differential equation of glucose dynamics, enabling end-to-end training. On simulated data, our approach is able to closely approximate true absorption rates, resulting in better forecast than heuristic parameterizations, despite only observing glucose, insulin, and macronutritional information. Our work readily generalizes to meal events with higher-dimensional covariates, such as images, setting the stage for glucose dynamics models that are personalized to each individual's daily life.

A Framework for Machine Learning of Model Error in Dynamical Systems

The development of data-informed predictive models for dynamical systems is of widespread interest in many disciplines. We present a unifying framework for blending mechanistic and machine-learning approaches to identify dynamical systems from data. We compare pure data-driven learning with hybrid models which incorporate imperfect domain knowledge. We cast the problem in both continuous- and discrete-time, for problems in which the model error is memoryless and in which it has significant memory, and we compare data-driven and hybrid approaches experimentally. Our formulation is agnostic to the chosen machine learning model. Using Lorenz '63 and Lorenz '96 Multiscale systems, we find that hybrid methods substantially outperform solely data-driven approaches in terms of data hunger, demands for model complexity, and overall predictive performance. We also find that, while a continuous-time framing allows for robustness to irregular sampling and desirable domain-interpretability, a discrete-time framing can provide similar or better predictive performance, especially when data are undersampled and the vector field cannot be resolved. We study model error from the learning theory perspective, defining excess risk and generalization error; for a linear model of the error used to learn about ergodic dynamical systems, both errors are bounded by terms that diminish with the square-root of T. We also illustrate scenarios that benefit from modeling with memory, proving that continuous-time recurrent neural networks (RNNs) can, in principle, learn memory-dependent model error and reconstruct the original system arbitrarily well; numerical results depict challenges in representing memory by this approach. We also connect RNNs to reservoir computing and thereby relate the learning of memory-dependent error to recent work on supervised learning between Banach spaces using random features.

Behavioral-clinical phenotyping with type 2 diabetes self-monitoring data

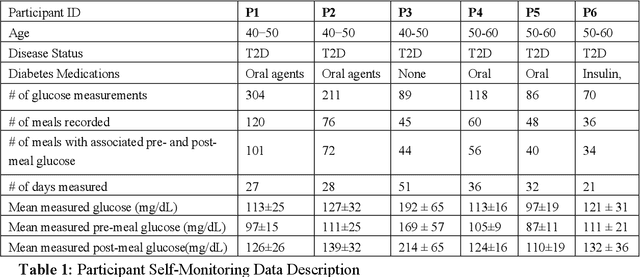
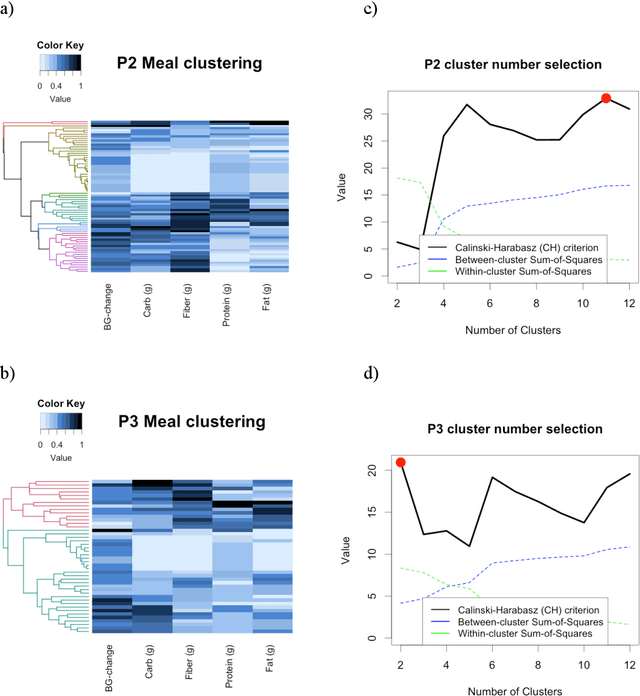
Objective: To evaluate unsupervised clustering methods for identifying individual-level behavioral-clinical phenotypes that relate personal biomarkers and behavioral traits in type 2 diabetes (T2DM) self-monitoring data. Materials and Methods: We used hierarchical clustering (HC) to identify groups of meals with similar nutrition and glycemic impact for 6 individuals with T2DM who collected self-monitoring data. We evaluated clusters on: 1) correspondence to gold standards generated by certified diabetes educators (CDEs) for 3 participants; 2) face validity, rated by CDEs, and 3) impact on CDEs' ability to identify patterns for another 3 participants. Results: Gold standard (GS) included 9 patterns across 3 participants. Of these, all 9 were re-discovered using HC: 4 GS patterns were consistent with patterns identified by HC (over 50% of meals in a cluster followed the pattern); another 5 were included as sub-groups in broader clusers. 50% (9/18) of clusters were rated over 3 on 5-point Likert scale for validity, significance, and being actionable. After reviewing clusters, CDEs identified patterns that were more consistent with data (70% reduction in contradictions between patterns and participants' records). Discussion: Hierarchical clustering of blood glucose and macronutrient consumption appears suitable for discovering behavioral-clinical phenotypes in T2DM. Most clusters corresponded to gold standard and were rated positively by CDEs for face validity. Cluster visualizations helped CDEs identify more robust patterns in nutrition and glycemic impact, creating new possibilities for visual analytic solutions. Conclusion: Machine learning methods can use diabetes self-monitoring data to create personalized behavioral-clinical phenotypes, which may prove useful for delivering personalized medicine.