Learning Explainable Treatment Policies with Clinician-Informed Representations: A Practical Approach

Digital health interventions (DHIs) and remote patient monitoring (RPM) have shown great potential in improving chronic disease management through personalized care. However, barriers like limited efficacy and workload concerns hinder adoption of existing DHIs; while limited sample sizes and lack of interpretability limit the effectiveness and adoption of purely black-box algorithmic DHIs. In this paper, we address these challenges by developing a pipeline for learning explainable treatment policies for RPM-enabled DHIs. We apply our approach in the real-world setting of RPM using a DHI to improve glycemic control of youth with type 1 diabetes. Our main contribution is to reveal the importance of clinical domain knowledge in developing state and action representations for effective, efficient, and interpretable targeting policies. We observe that policies learned from clinician-informed representations are significantly more efficacious and efficient than policies learned from black-box representations. This work emphasizes the importance of collaboration between ML researchers and clinicians for developing effective DHIs in the real world.

Hybrid Square Neural ODE Causal Modeling

Hybrid models combine mechanistic ODE-based dynamics with flexible and expressive neural network components. Such models have grown rapidly in popularity, especially in scientific domains where such ODE-based modeling offers important interpretability and validated causal grounding (e.g., for counterfactual reasoning). The incorporation of mechanistic models also provides inductive bias in standard blackbox modeling approaches, critical when learning from small datasets or partially observed, complex systems. Unfortunately, as hybrid models become more flexible, the causal grounding provided by the mechanistic model can quickly be lost. We address this problem by leveraging another common source of domain knowledge: ranking of treatment effects for a set of interventions, even if the precise treatment effect is unknown. We encode this information in a causal loss that we combine with the standard predictive loss to arrive at a hybrid loss that biases our learning towards causally valid hybrid models. We demonstrate our ability to achieve a win-win -- state-of-the-art predictive performance and causal validity -- in the challenging task of modeling glucose dynamics during exercise.

Online Learning for Traffic Routing under Unknown Preferences

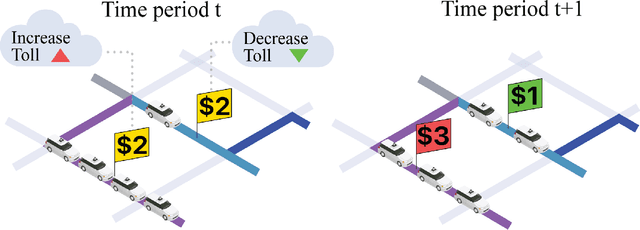
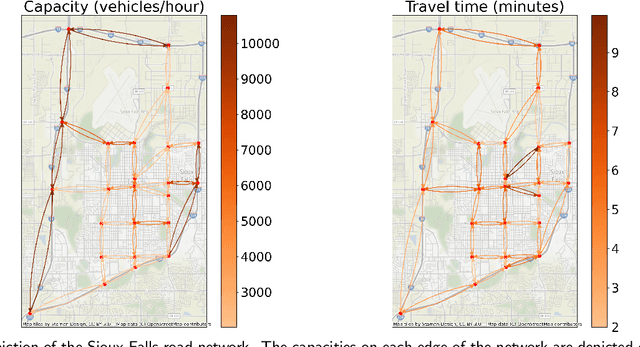
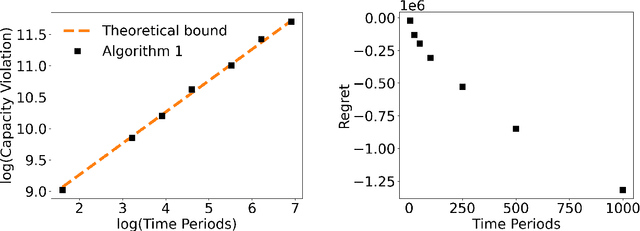
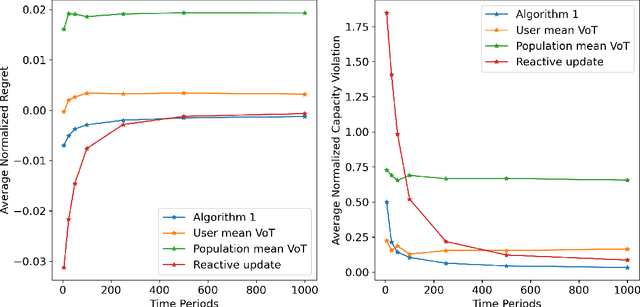
In transportation networks, users typically choose routes in a decentralized and self-interested manner to minimize their individual travel costs, which, in practice, often results in inefficient overall outcomes for society. As a result, there has been a growing interest in designing road tolling schemes to cope with these efficiency losses and steer users toward a system-efficient traffic pattern. However, the efficacy of road tolling schemes often relies on having access to complete information on users' trip attributes, such as their origin-destination (O-D) travel information and their values of time, which may not be available in practice. Motivated by this practical consideration, we propose an online learning approach to set tolls in a traffic network to drive heterogeneous users with different values of time toward a system-efficient traffic pattern. In particular, we develop a simple yet effective algorithm that adjusts tolls at each time period solely based on the observed aggregate flows on the roads of the network without relying on any additional trip attributes of users, thereby preserving user privacy. In the setting where the O-D pairs and values of time of users are drawn i.i.d. at each period, we show that our approach obtains an expected regret and road capacity violation of $O(\sqrt{T})$, where $T$ is the number of periods over which tolls are updated. Our regret guarantee is relative to an offline oracle that has complete information on users' trip attributes. We further establish a $\Omega(\sqrt{T})$ lower bound on the regret of any algorithm, which establishes that our algorithm is optimal up to constants. Finally, we demonstrate the superior performance of our approach relative to several benchmarks on a real-world transportation network, thereby highlighting its practical applicability.

Optimal and Greedy Algorithms for Multi-Armed Bandits with Many Arms

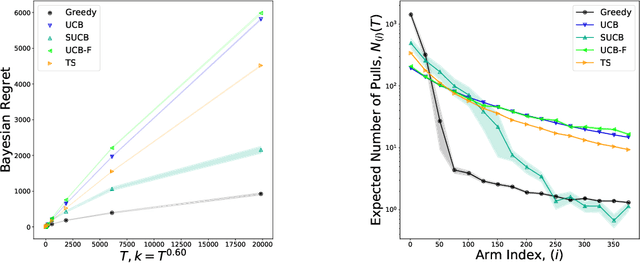
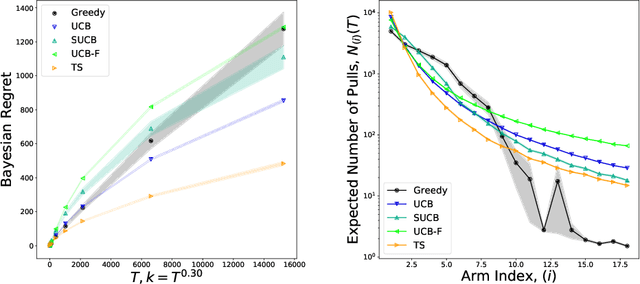
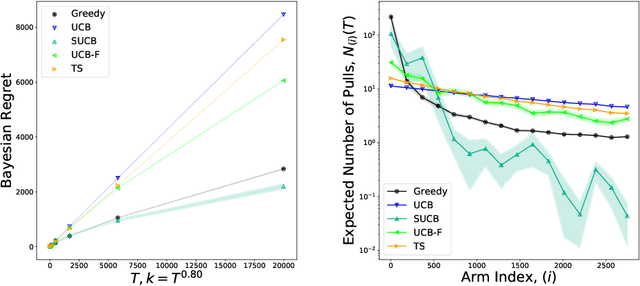
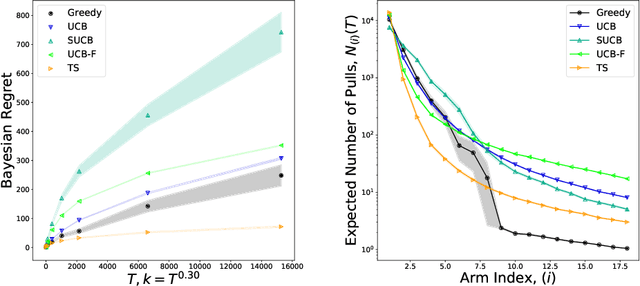
We characterize Bayesian regret in a stochastic multi-armed bandit problem with a large but finite number of arms. In particular, we assume the number of arms $k$ is $T^{\alpha}$, where $T$ is the time-horizon and $\alpha$ is in $(0,1)$. We consider a Bayesian setting where the reward distribution of each arm is drawn independently from a common prior, and provide a complete analysis of expected regret with respect to this prior. Our results exhibit a sharp distinction around $\alpha = 1/2$. When $\alpha < 1/2$, the fundamental lower bound on regret is $\Omega(k)$; and it is achieved by a standard UCB algorithm. When $\alpha > 1/2$, the fundamental lower bound on regret is $\Omega(\sqrt{T})$, and it is achieved by an algorithm that first subsamples $\sqrt{T}$ arms uniformly at random, then runs UCB on just this subset. Interestingly, we also find that a sufficiently large number of arms allows the decision-maker to benefit from "free" exploration if she simply uses a greedy algorithm. In particular, this greedy algorithm exhibits a regret of $\tilde{O}(\max(k,T/\sqrt{k}))$, which translates to a {\em sublinear} (though not optimal) regret in the time horizon. We show empirically that this is because the greedy algorithm rapidly disposes of underperforming arms, a beneficial trait in the many-armed regime. Technically, our analysis of the greedy algorithm involves a novel application of the Lundberg inequality, an upper bound for the ruin probability of a random walk; this approach may be of independent interest.

Semi-parametric dynamic contextual pricing

We consider a canonical revenue maximization problem where customers arrive sequentially; each customer is interested in buying one product, and the customer purchases the product if her valuation for it exceeds the price set by the seller. The valuations of customers are not observed by the seller; however, the seller can leverage contextual information available to her in the form of noisy covariate vectors describing the customer's history and the product's type to set prices. The seller can learn the relationship between covariates and customer valuations by experimenting with prices and observing transaction outcomes. We consider a semi-parametric model where the relationship between the expectation of the log of valuation and the covariates is linear (hence parametric) and the residual uncertainty distribution, i.e., the noise distribution, is non-parametric. We develop a pricing policy, DEEP-C, which learns this relationship with minimal exploration and in turn achieves optimal regret asymptotically in the time horizon.

Designing Optimal Binary Rating Systems

Modern online platforms rely on effective rating systems to learn about items. We consider the optimal design of rating systems that collect {\em binary feedback} after transactions. We make three contributions. First, we formalize the performance of a rating system as the speed with which it recovers the true underlying ranking on items (in a large deviations sense), accounting for both items' underlying match rates and the platform's preferences. Second, we provide an efficient algorithm to compute the binary feedback system that yields the highest such performance. Finally, we show how this theoretical perspective can be used to empirically design an implementable, approximately optimal rating system, and validate our approach using real-world experimental data collected on Amazon Mechanical Turk.

Bandit Learning with Positive Externalities

In many platforms, user arrivals exhibit a self-reinforcing behavior: future user arrivals are likely to have preferences similar to users who were satisfied in the past. In other words, arrivals exhibit positive externalities. We study multiarmed bandit (MAB) problems with positive externalities. We show that the self-reinforcing preferences may lead standard benchmark algorithms such as UCB to exhibit linear regret. We develop a new algorithm, Balanced Exploration (BE), which explores arms carefully to avoid suboptimal convergence of arrivals before sufficient evidence is gathered. We also introduce an adaptive variant of BE which successively eliminates suboptimal arms. We analyze their asymptotic regret, and establish optimality by showing that no algorithm can perform better.

Exploration vs. Exploitation in Team Formation

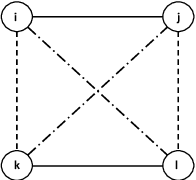
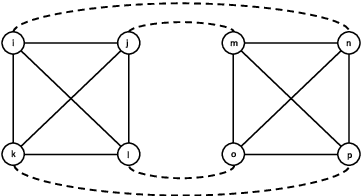
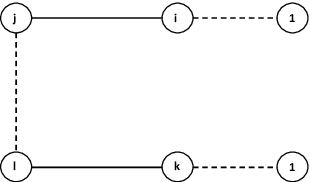
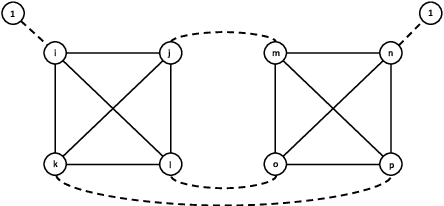
An online labor platform faces an online learning problem in matching workers with jobs and using the performance on these jobs to create better future matches. This learning problem is complicated by the rise of complex tasks on these platforms, such as web development and product design, that require a team of workers to complete. The success of a job is now a function of the skills and contributions of all workers involved, which may be unknown to both the platform and the client who posted the job. These team matchings result in a structured correlation between what is known about the individuals and this information can be utilized to create better future matches. We analyze two natural settings where the performance of a team is dictated by its strongest and its weakest member, respectively. We find that both problems pose an exploration-exploitation tradeoff between learning the performance of untested teams and repeating previously tested teams that resulted in a good performance. We establish fundamental regret bounds and design near-optimal algorithms that uncover several insights into these tradeoffs.

Matching while Learning

We consider the problem faced by a service platform that needs to match supply with demand, but also to learn attributes of new arrivals in order to match them better in the future. We introduce a benchmark model with heterogeneous workers and jobs that arrive over time. Job types are known to the platform, but worker types are unknown and must be learned by observing match outcomes. Workers depart after performing a certain number of jobs. The payoff from a match depends on the pair of types and the goal is to maximize the steady-state rate of accumulation of payoff. Our main contribution is a complete characterization of the structure of the optimal policy in the limit that each worker performs many jobs. The platform faces a trade-off for each worker between myopically maximizing payoffs (exploitation) and learning the type of the worker (\emph{exploration}). This creates a multitude of multi-armed bandit problems, one for each worker, coupled together by the constraint on the availability of jobs of different types (capacity constraints). We find that the platform should estimate a shadow price for each job type, and use the payoffs adjusted by these prices, first, to determine its learning goals and then, for each worker, (i) to balance learning with payoffs during the "exploration phase", and (ii) to myopically match after it has achieved its learning goals during the "exploitation phase."

Optimal Testing in the Experiment-rich Regime

Motivated by the widespread adoption of large-scale A/B testing in industry, we propose a new experimentation framework for the setting where potential experiments are abundant (i.e., many hypotheses are available to test), and observations are costly; we refer to this as the experiment-rich regime. Such scenarios require the experimenter to internalize the opportunity cost of assigning a sample to a particular experiment. We fully characterize the optimal policy and give an algorithm to compute it. Furthermore, we develop a simple heuristic that also provides intuition for the optimal policy. We use simulations based on real data to compare both the optimal algorithm and the heuristic to other natural alternative experimental design frameworks. In particular, we discuss the paradox of power: high-powered classical tests can lead to highly inefficient sampling in the experiment-rich regime.