Taming Wild Price Fluctuations: Monotone Stochastic Convex Optimization with Bandit Feedback

Prices generated by automated price experimentation algorithms often display wild fluctuations, leading to unfavorable customer perceptions and violations of individual fairness: e.g., the price seen by a customer can be significantly higher than what was seen by her predecessors, only to fall once again later. To address this concern, we propose demand learning under a monotonicity constraint on the sequence of prices, within the framework of stochastic convex optimization with bandit feedback. Our main contribution is the design of the first sublinear-regret algorithms for monotonic price experimentation for smooth and strongly concave revenue functions under noisy as well as noiseless bandit feedback. The monotonicity constraint presents a unique challenge: since any increase (or decrease) in the decision-levels is final, an algorithm needs to be cautious in its exploration to avoid over-shooting the optimum. At the same time, minimizing regret requires that progress be made towards the optimum at a sufficient pace. Balancing these two goals is particularly challenging under noisy feedback, where obtaining sufficiently accurate gradient estimates is expensive. Our key innovation is to utilize conservative gradient estimates to adaptively tailor the degree of caution to local gradient information, being aggressive far from the optimum and being increasingly cautious as the prices approach the optimum. Importantly, we show that our algorithms guarantee the same regret rates (up to logarithmic factors) as the best achievable rates of regret without the monotonicity requirement.

Grooming a Single Bandit Arm

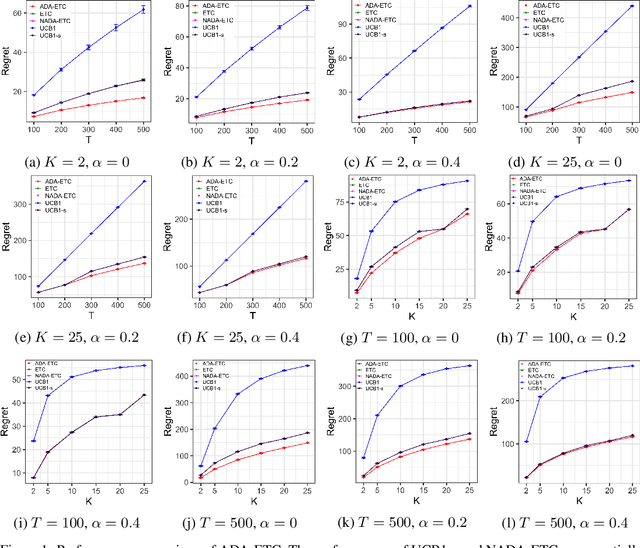
The stochastic multi-armed bandit problem captures the fundamental exploration vs. exploitation tradeoff inherent in online decision-making in uncertain settings. However, in several applications, the traditional objective of maximizing the expected sum of rewards obtained can be inappropriate. Motivated by the problem of optimizing job assignments to groom novice workers with unknown trainability in labor platforms, we consider a new objective in the classical setup. Instead of maximizing the expected total reward from $T$ pulls, we consider the vector of cumulative rewards earned from each of the $K$ arms at the end of $T$ pulls, and aim to maximize the expected value of the $highest$ cumulative reward. This corresponds to the objective of grooming a single, highly skilled worker using a limited supply of training jobs. For this new objective, we show that any policy must incur a regret of $\Omega(K^{1/3}T^{2/3})$ in the worst case. We design an explore-then-commit policy featuring exploration based on finely tuned confidence bounds on the mean reward and an adaptive stopping criterion, which adapts to the problem difficulty and guarantees a regret of $O(K^{1/3}T^{2/3}\sqrt{\log K})$ in the worst case. Our numerical experiments demonstrate that this policy improves upon several natural candidate policies for this setting.

Temporal Aspects of Individual Fairness

The concept of individual fairness advocates similar treatment of similar individuals to ensure equality in treatment [Dwork et al. 2012]. In this paper, we extend this notion to account for the time at which a decision is made, in settings where there exists a notion of "conduciveness" of decisions as perceived by individuals. We introduce two definitions: (i) fairness-across-time and (ii) fairness-in-hindsight. In the former, treatments of individuals are required to be individually fair relative to the past as well as future, while in the latter we only require individual fairness relative to the past. We show that these two definitions can have drastically different implications in the setting where the principal needs to learn the utility model: one can achieve a vanishing asymptotic loss in long-run average utility relative to the full-information optimum under the fairness-in-hindsight constraint, whereas this asymptotic loss can be bounded away from zero under the fairness-across-time constraint.

Exploration vs. Exploitation in Team Formation

An online labor platform faces an online learning problem in matching workers with jobs and using the performance on these jobs to create better future matches. This learning problem is complicated by the rise of complex tasks on these platforms, such as web development and product design, that require a team of workers to complete. The success of a job is now a function of the skills and contributions of all workers involved, which may be unknown to both the platform and the client who posted the job. These team matchings result in a structured correlation between what is known about the individuals and this information can be utilized to create better future matches. We analyze two natural settings where the performance of a team is dictated by its strongest and its weakest member, respectively. We find that both problems pose an exploration-exploitation tradeoff between learning the performance of untested teams and repeating previously tested teams that resulted in a good performance. We establish fundamental regret bounds and design near-optimal algorithms that uncover several insights into these tradeoffs.

Matching while Learning

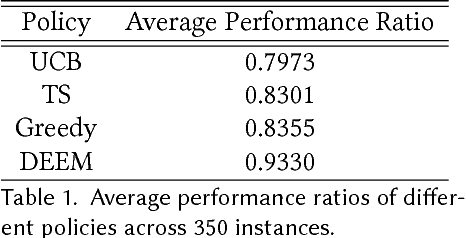
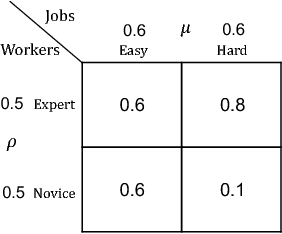
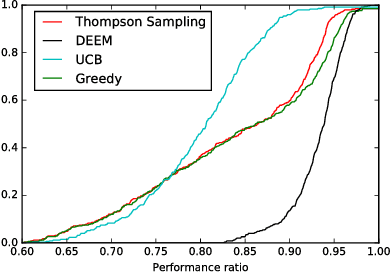
We consider the problem faced by a service platform that needs to match supply with demand, but also to learn attributes of new arrivals in order to match them better in the future. We introduce a benchmark model with heterogeneous workers and jobs that arrive over time. Job types are known to the platform, but worker types are unknown and must be learned by observing match outcomes. Workers depart after performing a certain number of jobs. The payoff from a match depends on the pair of types and the goal is to maximize the steady-state rate of accumulation of payoff. Our main contribution is a complete characterization of the structure of the optimal policy in the limit that each worker performs many jobs. The platform faces a trade-off for each worker between myopically maximizing payoffs (exploitation) and learning the type of the worker (\emph{exploration}). This creates a multitude of multi-armed bandit problems, one for each worker, coupled together by the constraint on the availability of jobs of different types (capacity constraints). We find that the platform should estimate a shadow price for each job type, and use the payoffs adjusted by these prices, first, to determine its learning goals and then, for each worker, (i) to balance learning with payoffs during the "exploration phase", and (ii) to myopically match after it has achieved its learning goals during the "exploitation phase."

An Approximate Dynamic Programming Approach to Repeated Games with Vector Losses

We describe an approximate dynamic programming (ADP) approach to compute approximately optimal strategies and approximations of the minimal losses that can be guaranteed in discounted repeated games with vector losses. At the core of our approach is a characterization of the lower Pareto frontier of the set of expected losses that a player can guarantee in these games as the unique fixed point of a set-valued dynamic programming (DP) operator. This fixed point can be approximated by an iterative application of this DP operator compounded by a polytopic set approximation, beginning with a single point. Each iteration can be computed by solving a set of linear programs corresponding to the vertices of the polytope. We derive rigorous bounds on the error of the resulting approximation and the performance of the corresponding approximately optimal strategies. We discuss an application to regret minimization in repeated decision-making in adversarial environments, where we show that this approach can be used to compute approximately optimal strategies and approximations of the minimax optimal regret when the action sets are finite. We illustrate this approach by computing provably approximately optimal strategies for the problem of prediction using expert advice under discounted $\{0,1\}-$losses. Our numerical evaluations demonstrate the sub-optimality of well-known off-the-shelf online learning algorithms like Hedge and a significantly improved performance on using our approximately optimal strategies in these settings. Our work thus demonstrates the significant potential in using the ADP framework to design effective online learning algorithms.

A Truth Serum for Large-Scale Evaluations

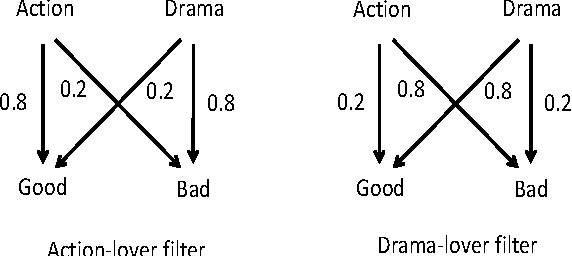
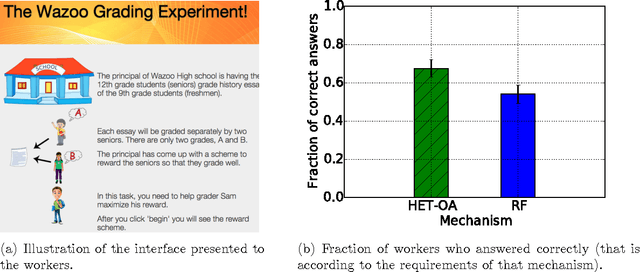
A major challenge in obtaining large-scale evaluations, e.g., product or service reviews on online platforms, labeling images, grading in online courses, etc., is that of eliciting honest responses from agents in the absence of verifiability. We propose a new reward mechanism with strong incentive properties applicable in a wide variety of such settings. This mechanism has a simple and intuitive output agreement structure: an agent gets a reward only if her response for an evaluation matches that of her peer. But instead of the reward being the same across different answers, it is inversely proportional to a popularity index of each answer. This index is a second order population statistic that captures how frequently two agents performing the same evaluation agree on the particular answer. Rare agreements thus earn a higher reward than agreements that are relatively more common. In the regime where there are a large number of evaluation tasks, we show that truthful behavior is a strict Bayes-Nash equilibrium of the game induced by the mechanism. Further, we show that the truthful equilibrium is approximately optimal in terms of expected payoffs to the agents across all symmetric equilibria, where the approximation error vanishes in the number of evaluation tasks. Moreover, under a mild condition on strategy space, we show that any symmetric equilibrium that gives a higher expected payoff than the truthful equilibrium must be close to being fully informative if the number of evaluations is large. These last two results are driven by a new notion of an agreement measure that is shown to be monotonic in information loss. This notion and its properties are of independent interest.

Sequential Relevance Maximization with Binary Feedback

Motivated by online settings where users can provide explicit feedback about the relevance of products that are sequentially presented to them, we look at the recommendation process as a problem of dynamically optimizing this relevance feedback. Such an algorithm optimizes the fine tradeoff between presenting the products that are most likely to be relevant, and learning the preferences of the user so that more relevant recommendations can be made in the future. We assume a standard predictive model inspired by collaborative filtering, in which a user is sampled from a distribution over a set of possible types. For every product category, each type has an associated relevance feedback that is assumed to be binary: the category is either relevant or irrelevant. Assuming that the user stays for each additional recommendation opportunity with probability $\beta$ independent of the past, the problem is to find a policy that maximizes the expected number of recommendations that are deemed relevant in a session. We analyze this problem and prove key structural properties of the optimal policy. Based on these properties, we first present an algorithm that strikes a balance between recursion and dynamic programming to compute this policy. We further propose and analyze two heuristic policies: a `farsighted' greedy policy that attains at least $1-\beta$ factor of the optimal payoff, and a naive greedy policy that attains at least $\frac{1-\beta}{1+\beta}$ factor of the optimal payoff in the worst case. Extensive simulations show that these heuristics are very close to optimal in practice.