Toward the Fundamental Limits of Imitation Learning

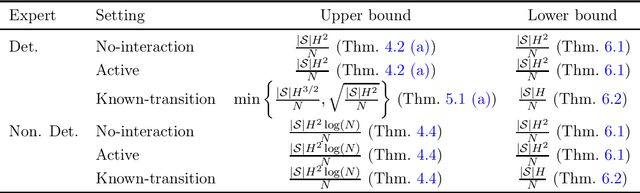
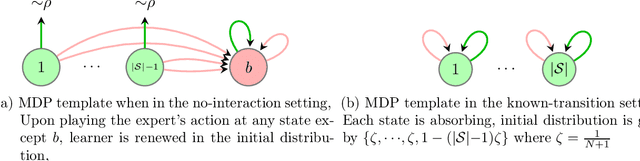
Imitation learning (IL) aims to mimic the behavior of an expert policy in a sequential decision-making problem given only demonstrations. In this paper, we focus on understanding the minimax statistical limits of IL in episodic Markov Decision Processes (MDPs). We first consider the setting where the learner is provided a dataset of $N$ expert trajectories ahead of time, and cannot interact with the MDP. Here, we show that the policy which mimics the expert whenever possible is in expectation $\lesssim \frac{|\mathcal{S}| H^2 \log (N)}{N}$ suboptimal compared to the value of the expert, even when the expert follows an arbitrary stochastic policy. Here $\mathcal{S}$ is the state space, and $H$ is the length of the episode. Furthermore, we establish a suboptimality lower bound of $\gtrsim |\mathcal{S}| H^2 / N$ which applies even if the expert is constrained to be deterministic, or if the learner is allowed to actively query the expert at visited states while interacting with the MDP for $N$ episodes. To our knowledge, this is the first algorithm with suboptimality having no dependence on the number of actions, under no additional assumptions. We then propose a novel algorithm based on minimum-distance functionals in the setting where the transition model is given and the expert is deterministic. The algorithm is suboptimal by $\lesssim \min \{ H \sqrt{|\mathcal{S}| / N} ,\ |\mathcal{S}| H^{3/2} / N \}$, showing that knowledge of transition improves the minimax rate by at least a $\sqrt{H}$ factor.

A Truth Serum for Large-Scale Evaluations

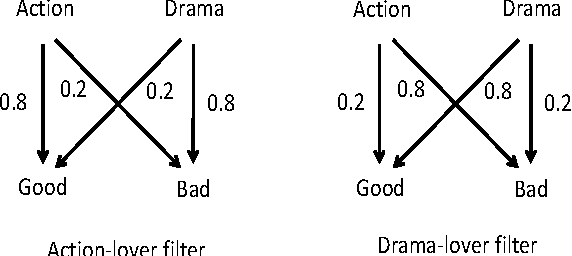
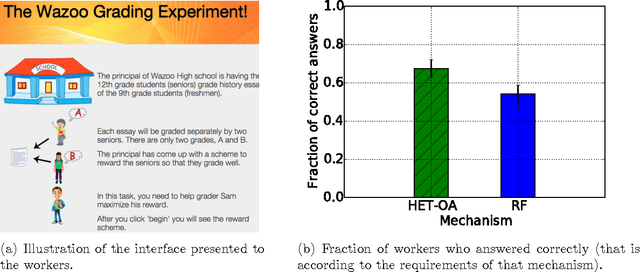
A major challenge in obtaining large-scale evaluations, e.g., product or service reviews on online platforms, labeling images, grading in online courses, etc., is that of eliciting honest responses from agents in the absence of verifiability. We propose a new reward mechanism with strong incentive properties applicable in a wide variety of such settings. This mechanism has a simple and intuitive output agreement structure: an agent gets a reward only if her response for an evaluation matches that of her peer. But instead of the reward being the same across different answers, it is inversely proportional to a popularity index of each answer. This index is a second order population statistic that captures how frequently two agents performing the same evaluation agree on the particular answer. Rare agreements thus earn a higher reward than agreements that are relatively more common. In the regime where there are a large number of evaluation tasks, we show that truthful behavior is a strict Bayes-Nash equilibrium of the game induced by the mechanism. Further, we show that the truthful equilibrium is approximately optimal in terms of expected payoffs to the agents across all symmetric equilibria, where the approximation error vanishes in the number of evaluation tasks. Moreover, under a mild condition on strategy space, we show that any symmetric equilibrium that gives a higher expected payoff than the truthful equilibrium must be close to being fully informative if the number of evaluations is large. These last two results are driven by a new notion of an agreement measure that is shown to be monotonic in information loss. This notion and its properties are of independent interest.