Abhay Parekh
A Truth Serum for Large-Scale Evaluations
Feb 16, 2018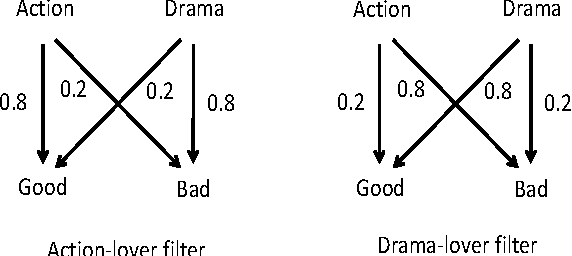
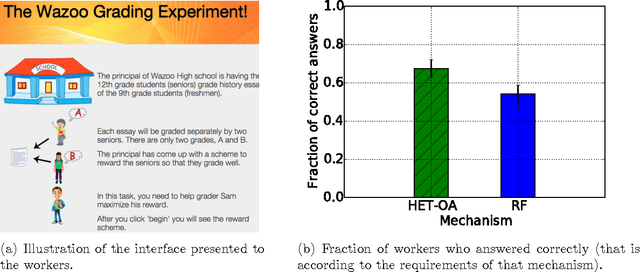
Abstract:A major challenge in obtaining large-scale evaluations, e.g., product or service reviews on online platforms, labeling images, grading in online courses, etc., is that of eliciting honest responses from agents in the absence of verifiability. We propose a new reward mechanism with strong incentive properties applicable in a wide variety of such settings. This mechanism has a simple and intuitive output agreement structure: an agent gets a reward only if her response for an evaluation matches that of her peer. But instead of the reward being the same across different answers, it is inversely proportional to a popularity index of each answer. This index is a second order population statistic that captures how frequently two agents performing the same evaluation agree on the particular answer. Rare agreements thus earn a higher reward than agreements that are relatively more common. In the regime where there are a large number of evaluation tasks, we show that truthful behavior is a strict Bayes-Nash equilibrium of the game induced by the mechanism. Further, we show that the truthful equilibrium is approximately optimal in terms of expected payoffs to the agents across all symmetric equilibria, where the approximation error vanishes in the number of evaluation tasks. Moreover, under a mild condition on strategy space, we show that any symmetric equilibrium that gives a higher expected payoff than the truthful equilibrium must be close to being fully informative if the number of evaluations is large. These last two results are driven by a new notion of an agreement measure that is shown to be monotonic in information loss. This notion and its properties are of independent interest.
Estimation from Pairwise Comparisons: Sharp Minimax Bounds with Topology Dependence
May 06, 2015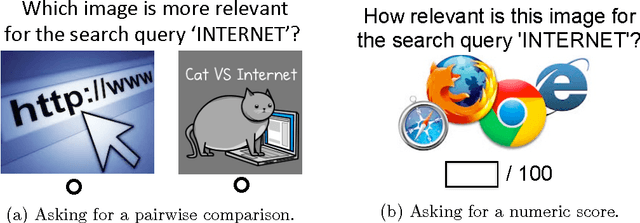
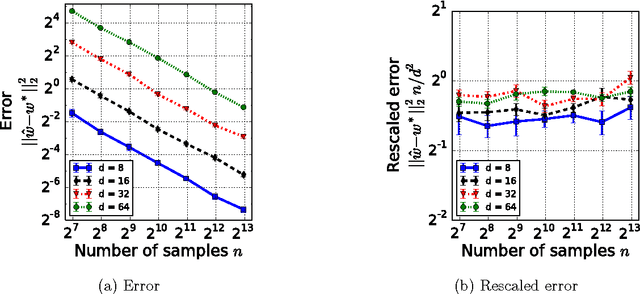

Abstract:Data in the form of pairwise comparisons arises in many domains, including preference elicitation, sporting competitions, and peer grading among others. We consider parametric ordinal models for such pairwise comparison data involving a latent vector $w^* \in \mathbb{R}^d$ that represents the "qualities" of the $d$ items being compared; this class of models includes the two most widely used parametric models--the Bradley-Terry-Luce (BTL) and the Thurstone models. Working within a standard minimax framework, we provide tight upper and lower bounds on the optimal error in estimating the quality score vector $w^*$ under this class of models. The bounds depend on the topology of the comparison graph induced by the subset of pairs being compared via its Laplacian spectrum. Thus, in settings where the subset of pairs may be chosen, our results provide principled guidelines for making this choice. Finally, we compare these error rates to those under cardinal measurement models and show that the error rates in the ordinal and cardinal settings have identical scalings apart from constant pre-factors.
When is it Better to Compare than to Score?
Jun 25, 2014

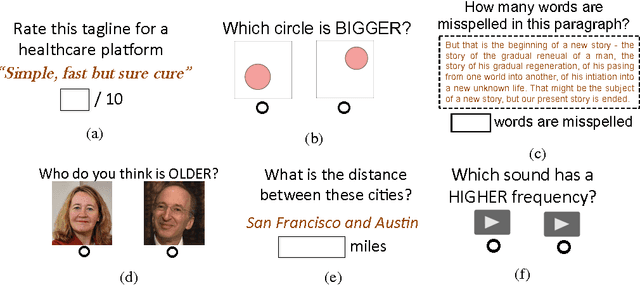

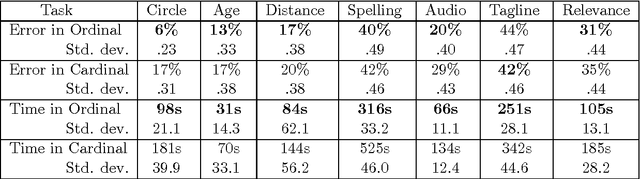
Abstract:When eliciting judgements from humans for an unknown quantity, one often has the choice of making direct-scoring (cardinal) or comparative (ordinal) measurements. In this paper we study the relative merits of either choice, providing empirical and theoretical guidelines for the selection of a measurement scheme. We provide empirical evidence based on experiments on Amazon Mechanical Turk that in a variety of tasks, (pairwise-comparative) ordinal measurements have lower per sample noise and are typically faster to elicit than cardinal ones. Ordinal measurements however typically provide less information. We then consider the popular Thurstone and Bradley-Terry-Luce (BTL) models for ordinal measurements and characterize the minimax error rates for estimating the unknown quantity. We compare these minimax error rates to those under cardinal measurement models and quantify for what noise levels ordinal measurements are better. Finally, we revisit the data collected from our experiments and show that fitting these models confirms this prediction: for tasks where the noise in ordinal measurements is sufficiently low, the ordinal approach results in smaller errors in the estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge